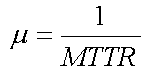
μは修復率です。
μ(件/時間)
=1/MTTR
=1/10(時間/件)
=0.1(件/時間)
答え0.1(件/時間)
ここでは、信頼性計算の方法を学びます。
下に行くに従って疲れてきてやる気がなくなっていったため、いい加減になってます(ぉぃ
表は、ある装置の故障件数と1件当たりの修復時間を示したものである。
| 1件当たりの修復時間(時間) | 件数 |
|---|---|
| 5 | 8 |
| 10 | 7 |
| 15 | 3 |
| 20 | 1 |
| 25 | 1 |
(i)総修復時間を求めよ。
(ii)MTTRを求めよ。
(iii)修復率を求めよ。
(iv)修復時間が指数分布に従うものとして、規定時間を10時間としたときの保全度を求めよ。
(i)総修復時間を求めよ。
5(時間)×8(件)+10(時間)×7(件)+15(時間)×3(件)+20(時間)×1(件)+25(時間)×1(件)
=200(時間)
答え200(時間)
(ii)MTTRを求めよ。
MTTR(時間/件)
=200(時間)/20(件)
=10(時間/件)
答え10(時間/件)
(iii)修復率を求めよ。
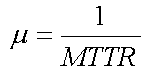
μは修復率です。
μ(件/時間)
=1/MTTR
=1/10(時間/件)
=0.1(件/時間)
答え0.1(件/時間)
(iv)修復時間が指数分布に従うものとして、規定時間を10時間としたときの保全度を求めよ。
問題文に指数分布に従うと書いてあった場合はすぐに下の式を思い出します。
M=1−e−μt
Mは保全度、μは修復率です。
M
=1−e−μt
=1−e−0.1×10
=1−e−1
=1−0.3703
=0.63
答え0.63
ある装置において、40ヶ月の故障件数を調べたところ8件あった。期間を1ヶ月、故障の発生は偶発的であるものとする。
(i)平均故障率λを求めよ。
(ii)信頼度Rを求めよ。
(i)平均故障率λを求めよ。
故障率(件/時間)
=8(件)/40(ヶ月)
=0.2(件/月)
答え0.2(件/月)
(ii)信頼度Rを求めよ。
故障は偶発的に起こるとあるので、故障の件数はポアソン分布に従います。
問題文に「偶発的」が出てきたらこれです。
R=e−λt
Rは信頼度、λは故障率、tは時間です。
R
=e−λt
=e−0.2(件/月)×1(ヶ月)
=e−0.2
=0.819
答え0.819
ある装置の稼働実績データを分析したところ、故障率が1.9×10−5(件/時間)の結果が得られた。この装置の10,000時間の信頼度Rはいくつですか?
とりあえず−λtを求めます。いきなり値を入れてもいいんですが、文字の大きさの関係で分けて計算してます(爆
λは故障率(件/時間)、tは時間です。
−λt
=−1.9×10−5(件/時間)×10,000(時間)
=−0.19(件)
R
=e−λt
=e−0.19
=0.827
答え0.827
装置A及び装置Bの平均故障率が、それぞれ0.0004(件/時間)と0.0003(件/時間)である。装置AとBの1000時間の信頼度RA及びRBを求めよ。
R=e−λt
Rは信頼度、λは故障率、tは時間です。
RA
=e−λt
=e−0.0004(件/時間)×1000(時間)
=e−0.4
=0.67
答え0.67
RB
=e−λt
=e−0.0003(件/時間)×1000(時間)
=e−0.3
=0.741
答え0.741
1,000個のメモリー素子を組み込んだ基盤がある。この基盤の100時間の信頼度が0.95であるとき、メモリー素子1個の故障率は、何フィット(FIT)か?
まず基盤の故障率を求めます。
R=e−λt
Rは信頼度、λは故障率、tは時間です。
R=e−λt (対数をとります(logを両辺にかけます))
logR=−λt (なんでこうなるかわからない方は信頼性計算のための数学(対数関数について)を参照)
log0.95=−λ×100
-0.05=−100λ
λ=0.0005
=5×10−4(件/時間)
この故障率は基盤の故障率です。基盤には1,000個のメモリー素子が組み込まれているので、メモリー素子1つ分の故障率は基盤の故障率の1/1000です(1/1000にする理由は信頼性計算のための数学(指数関数について)を参照)
よって、
5×10−4×1/1000
=5×10−7
ところで1FITは10−9(件/時間)なので、5×10−7は500FIT
答え500FIT
故障率が11000FITのユニットの2000時間の信頼度Rはいくつですか? 故障の発生は指数分布に従うものとします。
(筆者注 指数分布じゃなくて故障の発生は件数だからポアソン分布に従うと思ってみたり・・・指数分布はある故障が発生してから次の故障が発生するまでの時間の分布だったはず)
R=e−λt
Rは信頼度、λは故障率、tは時間です。
1FIT=10−9(件/時間)
11000FIT=11000×10−9
=0.000011(件/時間)
R=e−λt
=e−0.000011×2000
=e−0.022
=0.97824
答え0.98
ある装置の使用経過は表の通りであった。この装置の(i)MTBF (ii)MTTR (iii)アベイラビリティ を求めよ。
| 事項 | 経過時間(時間) |
|---|---|
| 使用開始 | 0 |
| 故障発生 | 160 |
| 故障回復 | 161 |
| 故障発生 | 310 |
| 故障回復 | 312 |
| 故障発生 | 459 |
| 故障回復 | 460 |
| 故障発生による使用終了 | 600 |
図にするとこんな感じです。
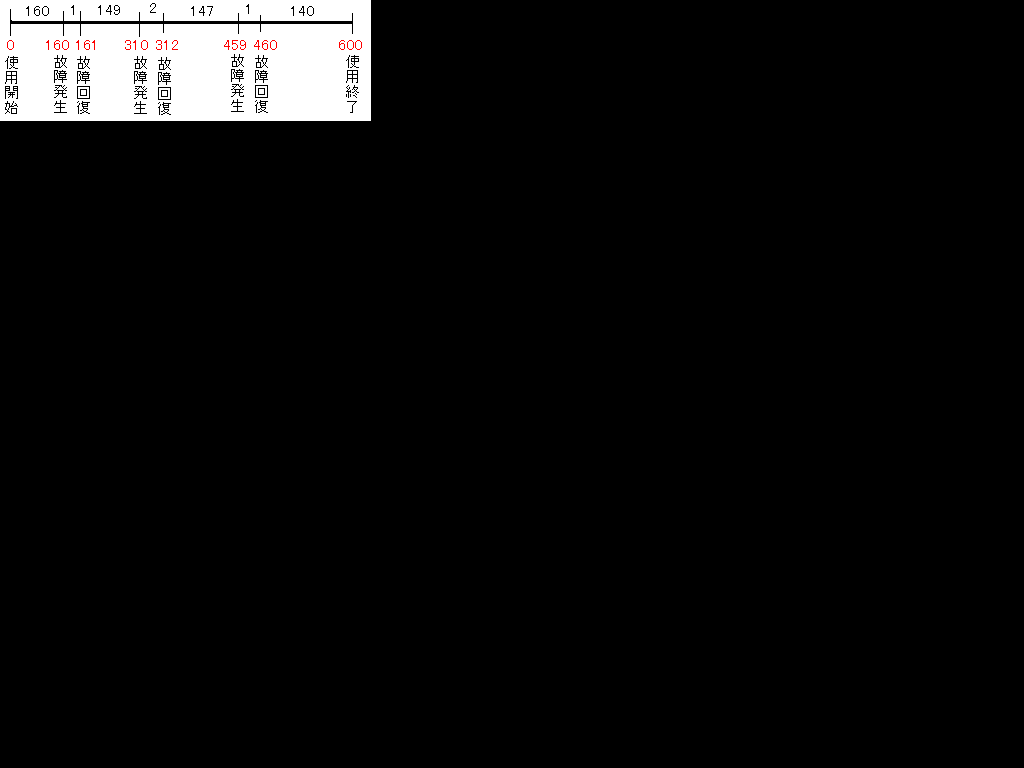
MTBF(時間/件)
=(160(時間)+149(時間)+147(時間)+140(時間))/4(件)
=149(時間/件)
答え149(時間/件)
MTTR(時間/件)
=(1(時間)+2(時間)+1(時間))/3(件)
=4/3(時間/件)
答え4/3(時間/件)
アベイラビリティ
=MTBF/(MTBF+MTTR)
=149/(149+4/3)
=0.99113
答え0.99
ある装置の稼働実績データを解析したところ、故障率λは0.1(件/時間)であり、修復率μは0.50(件/時間)であった。
(i)装置AのMTBFを求めよ。
(ii)装置AのMTTRを求めよ。
(iii)装置AのアベイラビリティAを求めよ。
(i)装置AのMTBFを求めよ。
MTBF(時間/件)=1/故障率(件/時間)
=1/0.1
=10(時間/件)
答え10(時間/件)
(ii)装置AのMTTRを求めよ。
MTTR(時間/件)=1/修復率(件/時間)
=1/0.50
=2(時間/件)
答え2(時間/件)
(iii)装置AのアベイラビリティAを求めよ。
アベイラビリティ
=MTBF/(MTBF+MTTR)
=10/(10+2)
=0.8333
答え0.8333
ある装置の保全データは以下の通りである。この装置Aの信頼性について答えよ。
| 総動作時間 | 192時間 |
| 総故障件数 | 3件 |
| 総修復時間 | 5.0時間 |
注 最後の故障の修復までのデータである。
(i)装置Aの平均故障率λを求めよ。
(ii)装置AのMTBFを求めよ。
(iii)装置AのMTTRを求めよ。
(iv)装置Aのアベイラビリティを求めよ。
イメージ図はこんな感じです。
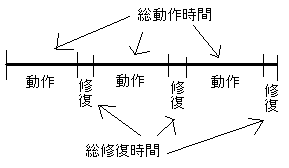
(i)装置Aの平均故障率λを求めよ。
平均故障率やMTBFを求める時の「時間」は「総動作時間」であり「修復している時間」は含みません。
平均故障率λ(件/時間)
=3(件)/192(時間)
=0.015625(件/時間)
答え0.015625(件/時間)
(ii)装置AのMTBFを求めよ。
MTBF(時間/件)
=192(時間)/3(件)
=64(時間/件)
答え64(時間/件)
(iii)装置AのMTTRを求めよ。
MTTR(時間/件)
=5.0(時間)/3(件)
=5/3(時間/件)
答え5/3(時間/件)
(iv)装置Aのアベイラビリティを求めよ。
アベイラビリティ
=MTBF/(MTBF+MTTR)
=64/(64+5/3)
=0.9746
答え0.9746
図は、装置Eの使用開始から4000時間までの故障発生と修復時間を示したものである。
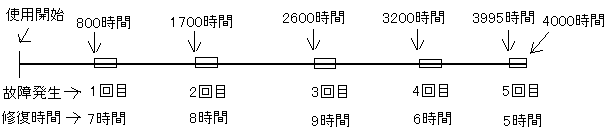
(i)装置Eの平均故障率λを求めよ。
(ii)装置EのMTBFを求めよ。
(iii)装置EのMTTRを求めよ。
(iv)装置Eのアベイラビリティを求めよ。
(i)装置Eの平均故障率λを求めよ。
この装置の総稼働時間は
4000(時間)−総修復時間
=4000−(7+8+9+6+5)
=3965(時間)
故障率λ(件/時間)
=5(件)/3965(時間)
=0.00126(件/時間)
答え0.00126(件/時間)
(ii)装置EのMTBFを求めよ。
MTBF(時間/件)
=1/故障率(件/時間)
=1/0.00126
=793(時間/件)
答え793(時間/件)
(iii)装置EのMTTRを求めよ。
MTTR(時間/件)
=(7+8+9+6+5)(時間)/5(件)
=7(時間/件)
答え7(時間/件)
(iv)装置Eのアベイラビリティを求めよ。
アベイラビリティ
=MTBF/(MTTR+MTBF)
=793/(7+793)
=0.99125
答え0.99125
復習
故障率 MTBF 不稼働率 信頼性計算のための数学(指数関数について)
偶発故障をする装置Aがある。この装置Aは、5つの基盤からなり、1つの基盤は1000個の部品から構成されている。1個の部品の単位時間(1時間)あたりの故障率は1.0×10−6であり、故障したときの装置Aの修復時間は2時間である。装置Aは1個でも部品が故障すれば動作しない。
(i)装置Aの故障率λを求めよ
(ii)装置AのMTBFを求めよ。
(iii)装置Aの不稼働率Wを求めよ。
(i)装置Aの故障率λを求めよ
イメージ図はこんな感じになります。
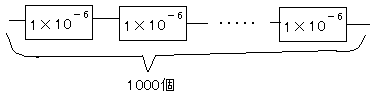
この基盤が5枚あります。
故障率は足します(理由は信頼性計算のための数学(指数関数について)ので、装置Aの故障率は
1.0×10−6×5(枚)×1000(個)
=5.0×10−3
答え5.0×10−3(件/時間) んー、htmlの仕様か・・・
(ii)装置AのMTBFを求めよ。
MTBF(時間/件)=1/故障率(件/時間)
=1/5.0×10−3
=200(時間/件)
答え200(時間/件)
(iii)装置Aの不稼働率Wを求めよ。
問題文に「故障したときの修復時間が2時間」とありますので、「故障1件あたり修復時間が2時間」と分かります。ということは「MTTRが2時間」ということです。
不稼働率W
=MTTR/(MTBF+MTTR)
=2/(200+2)
=0.0099
答え0.0099
5台の非修理系装置Aが、一斉に稼働を開始した。稼働開始後2000、5000、9000、13000、及び16000時間でそれぞれ故障した。
(i)装置AのMTTFを求めよ。
(ii)装置Aの稼働開始から8000時間及び稼働開始から15000時間における信頼度、R(8)及びR(15)求めよ。
(iii)装置Aの稼働開始から4000時間及び4000時間から8000時間の各時間帯の故障率、λ(4)及びλ(8)を求めよ。
この問題むずいです。
問題に指数分布に従うとか書いていないので、信頼度を求めるのにR=e−λtを使いません。
(i)装置AのMTTFを求めよ。
MTTF
=(2000+5000+9000+13000+16000)/5
=9000(時間/件)
答え9000(時間/件)
(ii)装置Aの稼働開始から8000時間及び稼働開始から15000時間における信頼度、R(8)及びR(15)求めよ。
信頼度というのは、ある時間に機械が動いている確率です。よって分布がわからない場合は、「ある時間に動いている機械の台数/総台数」です。
稼働開始から8000時間経って動いている機械は、5台中3台です。よって、R(8)は3/5です。
稼働開始から15000時間経って動いている機械は、5台中1台です。よって、R(15)は1/5です。
答え R(8)=3/5 R(15)=1/5
(iii)装置Aの稼働開始から4000時間及び4000時間から8000時間の各時間帯の故障率、λ(4)及びλ(8)を求めよ。
装置Aの稼働状態のイメージ図は下のようになります。
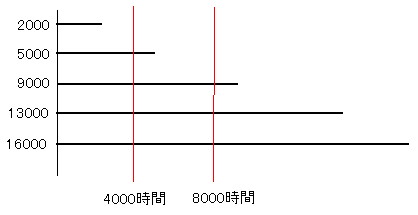
故障率は(件/時間)です。4000時間までは1件故障しているので分子は1です。分母の時間は5台の装置について4000時間を調べているので、5×4000(時間)です。
よって
故障率(件/時間)
=1/20000
=5.0×10−5(件/時間)
答え5.0×10−5(件/時間)
4000時間から8000時間に故障しているのは1件で時間はやっぱり4000(時間)×4(台)=16000(時間)なので(4000時間以降は動いている機械が4つ)故障率は
故障率=1/16000=6.3×10−5
答え6.3×10−5(件/時間)
装置Aの偶発故障データを調べたところ、表の結果を得た。最後に発生した故障の修理完了時が調査期間の終わりである。
| 総動作時間 | 10000時間 |
| 総故障件数 | 2件 |
| 総修復時間 | 10時間 |
(i)装置Aの故障率λを求めよ。
(ii)装置AのMTTRを求めよ。
(iii)装置Aの修復率μを求めよ。
(iv)装置Aの1000時間の信頼度Rを求めよ。
イメージはこんな感じです。
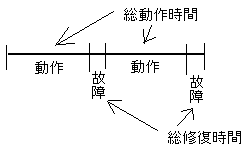
(i)装置Aの故障率λを求めよ。
故障率(件/時間)
=2(件)/10000(時間)
=0.0002(件/時間)
答え0.0002(件/時間)
(ii)装置AのMTTRを求めよ。
MTTR(時間/件)
=10(時間)/2(件)
=5(時間/件)
答え5(時間/件)
(iii)装置Aの修復率μを求めよ。
修復率μ(件/時間)
=1/MTTR(時間/件)
=1/5
=0.2(時間/件)
答え0.2(時間/件)
(iv)装置Aの1000時間の信頼度Rを求めよ。
信頼度R
=e−λt
=e−0.0002(件/時間)×1000(時間)
=e−0.2
=0.819
答え0.819
ある装置の故障率が2.5×10−4(件/時間)であるとき、MTBFを求めよ。またある装置の1000時間の信頼度を求めよ。
MTBF(時間/件)
=1/故障率(件/時間)
=1/2.5×10−4
=4000(時間/件)
答え4000(時間/件)
信頼度R
=e−λt
=exp(−2.5×10−4(件/時間)×1000(時間))
=exp(−0.25)
=0.7788
答え0.7788
次の表は装置Aのある期間内の動作状況を調べたものである。
| 総動作時間(時間) | 2000 |
| 総故障数(件) | 20 |
| 総修復時間(時間) | 200 |
(i)装置AのMTBFを求めよ。
(ii)装置Aの修復率μを求めよ。
(iii)装置Aのアベイラビリティを求めよ。
(iv)装置Aの修復着手後10時間の保全度Mを求めよ。
(i)装置AのMTBFを求めよ。
MTBF(時間/件)
=2000(時間)/20(件)
=100(時間/件)
答え100(時間/件)
(ii)装置Aの修復率μを求めよ。
修復率μ(件/時間)
=20(件)/200(時間)
=0.1(件/時間)
答え0.1(件/時間)
(iii)装置Aのアベイラビリティを求めよ。
まずMTTRを求めます。
MTTR(時間/件)
=1/修復率(件/時間)
=1/0.1(件/時間)
=10(時間/件)
アベイラビリティ
=MTBF/(MTBF+MTTR)
=100/(100+10)
=0.909
答え0.909
(iv)装置Aの修復着手後10時間の保全度Mを求めよ。
保全度M
=1−e−μt
=1−e−0.1(件/時間)×10(時間)
=1−e−1
=1−0.3678
=0.6322
答え0.6322
装置Eの保全データを調べたところ、MTBFは2000時間、MTTRは50時間であった。
(i)装置Eの故障率λを求めよ。
(ii)装置Eの修復率μを求めよ。
(iii)装置Eのアベイラビリティを求めよ。
(iv)装置Eの100時間の信頼度Rを求めよ。
(i)装置Eの故障率λを求めよ。
故障率(件/時間)
=1/MTBF(時間/件)
=1/2000
=0.005(件/時間)
答え0.005(件/時間)
(ii)装置Eの修復率μを求めよ。
修復率(件/時間)
=1/MTTR(時間/件)
=1/50
=0.02(件/時間)
答え0.02(件/時間)
(iii)装置Eのアベイラビリティを求めよ。
アベイラビリティ
=MTBF/(MTBF+MTTR)
=2000/(2000+50)
=0.9756
答え0.9756
(iv)装置Eの100時間の信頼度Rを求めよ。
信頼度R
=e−λt
=e−0.0005(件/時間)×100(時間)
=e−0.05
=0.9512
答え0.9512
装置Eの故障率λを20000(FIT)とするとき、10000時間の信頼度Rはいくつか?
まずFITを故障率になおします。(いや、FITも故障率の単位なんですけど・・・)
1FIT=10−9(件/時間)
20000FIT=20000×10−9(件/時間)
=0.00002(件/時間)
信頼度R
=e−λt
=e−0.00002(件/時間)×10000(時間)
=e−0.2
=0.8187
答え0.8187
ある装置Eのある期間の動作状況、修復状況を調査したところ、総故障件数は10件、総動作時間は120時間、修理のための総修復時間は5時間(最後に発生した故障の修復時間を含む)であった。故障の発生間隔は指数分布に従います。
(i)装置EのMTBFを求めよ。
(ii)装置EのMTTRを求めよ。
(iii)装置Eの故障率λを求めよ。
(iv)装置Eの不稼働率Wを求めよ。
(i)装置EのMTBFを求めよ。
MTBF(時間/件)
=120(時間)/10(件)
=12(時間/件)
答え12(時間/件)
(ii)装置EのMTTRを求めよ。
MTTR(時間/件)
=5(時間)/10(件)
=0.5(時間/件)
答え0.5(時間/件)
(iii)装置Eの故障率λを求めよ。
故障率λ(件/時間)
=1/MTBF(時間/件)
=1/12
=0.08333(件/時間)
答え0.08333(時間/件)
(iv)装置Eの不稼働率Wを求めよ。
不稼働率W
=MTTR/(MTBF+MTTR)
=0.5/(12+0.5)
=0.04
答え0.04
複数台の装置Aを用いたシステムの保全データから表1及び表2の結果が得られた。表1は、6台(装置記号a〜f)の装置Aの修復時間を示したものである。また、表2は、装置Aに使用されていた同一機能の部品Pで故障の直接原因となった5個(p〜t)の部品の動作開始から故障までの動作時間を示したものである。
| 装置記号 | 修復時間(時間) |
|---|---|
| a | 6 |
| b | 4 |
| c | 7 |
| d | 6 |
| e | 13 |
| f | 9 |
| 部品記号 | 故障までの動作時間(時間) |
|---|---|
| p | 12 000 |
| q | 23 000 |
| r | 17 000 |
| s | 8 000 |
| t | 28 000 |
(i)装置Aの修復着手後5時間における保全度Mを求めよ。
(ii)装置Aの修復着手後10時間における修復率μを求めよ。
(iii)部品Pの動作開始後20 000時間における信頼度Rを求めよ。
(iv)部品Pの動作開始後10 000時間における平均故障率λを求めよ。
(i)装置Aの修復着手後5時間における保全度Mを求めよ。
5時間後に治っているのはa〜fのうちで1つだけです。
よって保全度Mは
1(台)/6(台)=1/6
答え1/6
(ii)装置Aの修復着手後10時間における修復率μを求めよ。
修復率=修復件数/総修復時間
です。これを書いていてやっとわかったんですが、
修理系の故障率
=総故障件数/総稼働時間
非修理系の故障率
=単位時間の故障件数/(単位時間×調べた装置の件数)
分かりにくいんで、図で説明します。
たとえば、こんなデータがあったとします。
| 回数 | 稼働時間(時間) |
|---|---|
| 1 | 6 |
| 2 | 4 |
| 3 | 7 |
| 4 | 6 |
| 5 | 13 |
| 6 | 9 |
問題が10時間までの故障率を求めろ、となっていたとします。
これが修理系でしたら
修理系の故障率
=総故障件数/総稼働時間
で求めます。10時間までの総稼働時間は下の図での青い線の部分になります。
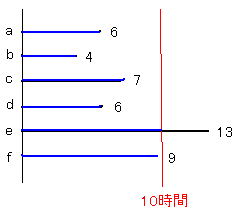
10時間までに5台故障しているので、
総故障件数/総稼働時間
=5(件)/(6+4+7+6+10+9)(時間)
=5(件)/42(時間)
=0.119(件/時間)
これが非修理系ですと
非修理系の故障率
=単位時間の故障件数/(単位時間×調べた装置の件数)
で求めます。「単位時間の故障件数」の「単位時間」は今回は10時間で、「故障件数」は「1件」、「調べた装置の数」は6つです。
よって
非修理系の故障率
=単位時間の故障件数/(単位時間×調べた装置の件数)
=5/(10×6)
=0.0833(件/時間)
話を戻します。
修復率は修理系でしか存在しません。なぜなら、非修理系は修復しないで部品自体を取り替えるからです。
よって修復率は
修復率=修復件数/総修復時間
です。
問題をもう一回書くと、
(ii)装置Aの修復着手後10時間における修復率μを求めよ。
| 装置記号 | 修復時間(時間) |
|---|---|
| a | 6 |
| b | 4 |
| c | 7 |
| d | 6 |
| e | 13 |
| f | 9 |
イメージ図はこんな感じです。

10時間までに5台が修復しており、修復にかかった時間は青い線の部分です。
修復率
=修復件数/総修復時間
=5(件)/(6+4+7+6+10+9)(時間)
=5(件)/42(時間)
=0.119(件/時間)
答え0.119(件/時間)
| 部品記号 | 故障までの動作時間(時間) |
|---|---|
| p | 12 000 |
| q | 23 000 |
| r | 17 000 |
| s | 8 000 |
| t | 28 000 |
(iii)部品Pの動作開始後20 000時間における信頼度Rを求めよ。
信頼度R
=(20 000時間後に動いている部品の件数)/(部品の数)
=2(件)/5(件)
=0.4
答え0.4
(iv)部品Pの動作開始後10 000時間における平均故障率λを求めよ。
こちらは部品を取り替えるので、非修理系です。
10 000時間で故障しているのは、sです。
非修理系の故障率
=単位時間の故障件数/(単位時間×調べた装置の件数)
=1(件)/(10 000(時間)×5(件))
=0.00002(件/時間)
答え0.00002(件/時間)