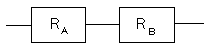
RAとRBは信頼度です。
この時のシステム全体の信頼度Rは
全体の信頼度R=RA×RB
直列モデル
直列モデルのみの問題
並列モデル
並列モデルのみの問題
演習問題1(全体の信頼度を求める編)
演習問題2(全体の信頼度から個々のシステムの信頼度を求める編)

RAとRBは信頼度です。
この時のシステム全体の信頼度Rは
全体の信頼度R=RA×RB

RAとRBとRCは信頼度です。
この時のシステム全体の信頼度Rは
R=RA×RB×RC
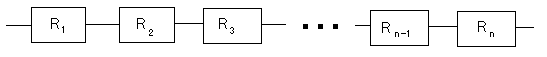
R1とR2とR3と・・・とRn-1とRnは信頼度です。
この時のシステム全体の信頼度Rは
R=R1×R2×R3×・・・×Rn-1×Rn
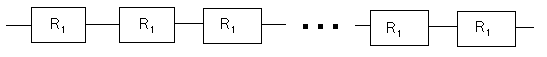
R1は信頼度です。
この時のシステム全体の信頼度Rは
R=(R1)n
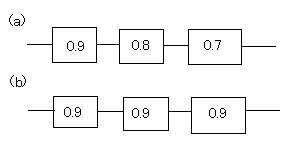
解答
(a) 0.9×0.8×0.7=0.504 答え0.504
(b) 0.9の3乗=0.729 答え0.729
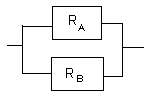
RAとRBは信頼度です。
この時のシステム全体の信頼度Rは
R=1−(1−RA)(1−RB)
ちなみに、この式は高校で習っているはずの「余事象」の概念から導出されます。かなり確率の基本です。
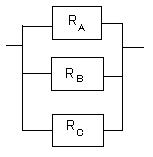
R1とR2とR3と・・・とRn-1とRnは信頼度です。
この時のシステム全体の信頼度Rは
R=1−(1−RA)(1−RB)(1−RC)
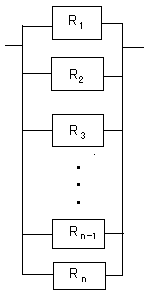
R1とR2とR3と・・・とRn-1とRnは信頼度です。
この時のシステム全体の信頼度Rは
R=1−(1−R1)(1−R2)(1−R3)・・・(1−Rn-1)(1−Rn)
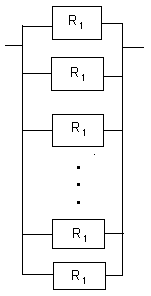
R1は信頼度です。
この時のシステム全体の信頼度Rは
R=1−(1−R1)n
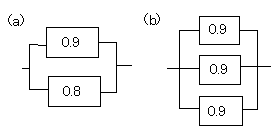
解答
(a) 1−(1−0.9)(1−0.8)=0.98 答え0.98
(b) 1−(1−0.9)3=0.999 答え0.999
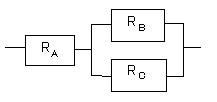
解法
分かるところから計算していきます。まず右の並列部分を計算します。
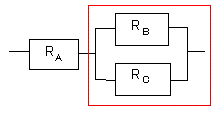
赤い部分の信頼度は、
1−(1−RB)(1−RC)
です。
そこで赤い部分を置き換えてみます。
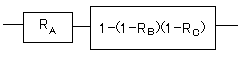
あとは直列モデルの計算です。
R=RA−RA(1−RB)(1−RC)
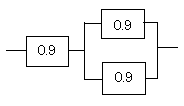
解法
分かるところから計算していきます。まず右の並列部分を計算します。
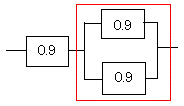
赤い部分の信頼度は
1−(1−0.9)(1−0.9)=0.99
と計算するか
1−(1−0.9)2=0.99
と計算とます。どちらで計算してもかまいません。
そこで赤い部分を置き換えてみます。
![]()
あとは直列モデルの計算です。
R=0.9×0.99=0.891
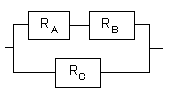
解法
分かるところから計算していきます。まず上の直列部分を計算します。
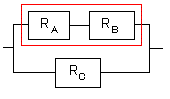
赤い部分の信頼度は
RA×RB=RARB
そこで赤い部分を置き換えてみます。
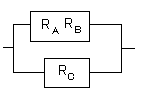
あとは並列モデルの計算です。
R=1−(1−RARB)(1−RC)
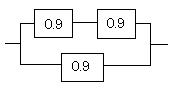
解法
分かるところから計算していきます。まず上の直列部分を計算します。
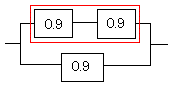
赤い部分の信頼度は
0.9×0.9=0.81
そこで赤い部分を置き換えてみます。
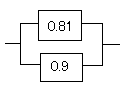
あとは並列モデルの計算です。
R=1−(1−0.81)(1−0.9)=0.981
(稼働率と信頼度はこの場合同義です)
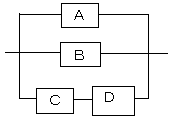
解法
このシステムは要するに以下のようになります。
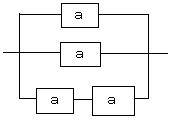
分かるところから計算していきます。まず一番下の段の直列部分を計算します。
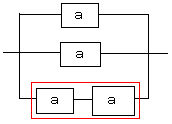
赤い部分の信頼度は
a×a=a2
そこで赤い部分を置き換えてみます。
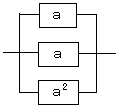
あとは並列モデルの計算です。
R=1−(1−a)(1−a)(1−a2)
=2a−2a3+a4
(稼働率と信頼度はこの場合同義です)
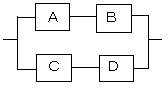
ちなみにこのシステムのことをシステム予備(系並列冗長)方式といいます。
解法
このシステムは要するに以下のようになります。
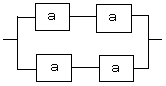
分かるところから計算していきます。まず直列部分を計算します。
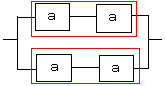
赤い部分の信頼度は上も下も同じで
a×a=a2
そこで赤い部分を置き換えてみます。
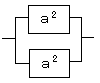
あとは並列モデルの計算です。
R=1−(1−a2)(1−a2)
=1−(1−a2)2
=2a2−a4
(稼働率と信頼度はこの場合同義です)
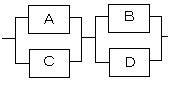
ちなみにこのシステムのことを装置予備(要素並列冗長)方式といいます。
解法
このシステムは要するに以下のようになります。
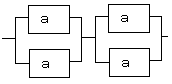
分かるところから計算していきます。まず並列部分を計算します。
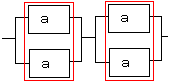
赤い部分の信頼度は右も左も同じで
1−(1−a)2
そこで赤い部分を置き換えてみます。
![]()
あとは直列モデルの計算です。
R=(1−(1−a)2)2
=4a2−4a3+a4
ところで、システム予備方式と装置予備方式はどちらが信頼度が高いのでしょうか?
これは、信頼度を引き算すれば分かります。
システム予備方式の信頼度は2a2−a4
装置予備方式の信頼度は4a2−4a3+a4
ですので、引き算すると
(装置予備方式)−(システム予備方式)
=4a2−4a3+a4−(2a2−a4)
=2a2−4a3+2a4
=2a2(1−2a+a2)
=2a2(1−a)2>0
aにどんな数値が入ってもこの式は正の数になります。
結果
(装置予備方式)−(システム予備方式)>0
なので、装置予備方式の信頼度の方が大きいと分かります。
図にするとこんな感じになります。
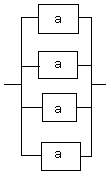
この中で3つ動いていればOK
並列モデルとは違います!! これはただのイメージ図です。
いままでやってきたのは、この4つのうち1つでも稼働していればOKというモデルでした。今回はこのうち3つが稼働していないと駄目です。
4つすべてが稼働している確率+3つが稼働している確率
を求めればよいです。
4つすべてが稼働している確率は、4つすべてが動いていないと駄目なので、以下の直列モデルと同じことです。
![]()
4つすべてが稼働している確率(稼働率)はa4
次に3つが稼働している確率を求めます。
3つが稼働しているということは、1つは故障しています。3つだけ動いて1つ故障している事例は次の4通りあります。
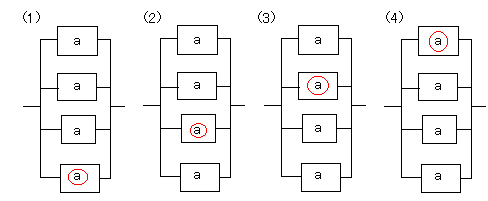
赤丸がついているのは、故障しているシステムです。
3つが稼働している確率は「3つ動いていて1つが故障している確率」です。
故障率=1−信頼度 で故障率は求まります。この場合、故障率は 1-a となります。
そんなわけで、3つが稼働しているモデルは以下の直列モデルになります。

3つが稼働している確率(稼働率)はa3(1−a)
これが4通りあるので、4倍して
4a3(1−a)
したがって、このシステムの稼働率は、
4つすべてが稼働している確率+3つが稼働している確率
=a4+4a3(1−a)
=4a3−3a4
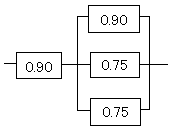
2/3冗長構成というのは、要するに3台のうち2台が稼働していればOKということです。
まず、右の並列部分の信頼度を求めます。
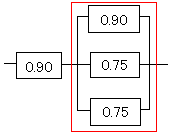
並列部分の信頼度は「3つすべてが動いている確率+いずれか2つが稼働している確率」です。
3つすべてが動いている確率は、以下の直列モデルと同じことです。
![]()
よって、0.90×0.75×0.75=0.50625
次にいずれか2つが稼働している確率を求めます。2つが稼働しているパターンは以下のように3つあります。
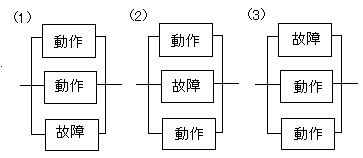
それぞれの場合についての確率を求めます。
(1)のようなパターンの確率は、一番上の装置が動いている確率が0.90、真ん中の装置が動いている確率が0.75、一番下の装置が故障している確率は 1−0.75=0.25 なので
0.90×0.75×0.25=0.16875

(2)のようなパターンの確率は、一番上の装置が動いている確率が0.90、真ん中の装置が故障している確率が 1−0.75=0.25、一番下の装置が動いている確率は0.75なので
0.90×0.25×0.75=0.16875
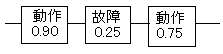
(3)のようなパターンの確率は、一番上の装置が故障している確率が1−0.90=0.10、真ん中の装置が動いている確率が0.75、一番下の装置が動いている確率は0.75なので
0.10×0.75×0.75=0.05625

よって、並列部分の信頼度は、
3つすべてが動いている確率+2つが稼働している確率
=0.50625+(0.16875+0.16875+0.05625)
=0.9
並列部分を0.9に置き換えると、
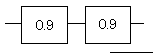
これは直列モデルなので、R=0.9×0.9=0.81
そんなわけで、某『98年版共通編電気通信主任技術者試験全問解答集』は間違ってます(笑
だって、どういうわけか並列部分の信頼度をみんな0.75として計算しているんだもん。0.90って書いてあるやんけ。
まー、信頼度が全部同じだと計算が楽になるから気持ちはわからんでもないけど。
東京−大阪間に信頼度が0.8の回線、東京−名古屋間に信頼度が0.7の回線がある。東京−大阪間の信頼度を0.9以上とするためには、名古屋−大阪間の回線の信頼度はいくつにしないと駄目か?
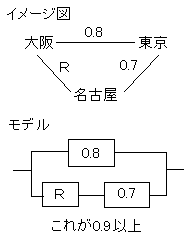
まず、モデルの信頼度を文字入りで求めます。分かる部分から計算しますので、直列部分を計算します。
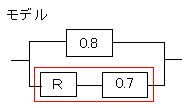
赤い部分の信頼度は
R×0.7=0.7R
赤い部分を0.7Rで置き換えます。
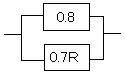
これは並列モデルなので、並列モデルでの計算をすると、
1−(1−0.8)(1−0.7R)
これが0.9より大きくなくてはいけないので、
1−(1−0.8)(1−0.7R)>0.9 (ホントは>=なんですけど、>で代用)
1−0.2(1−0.7R)>0.9
−0.2+0.14R>−0.1
0.14R>0.1
R>0.7142
この手の問題はあんまり出ていないみたいなので、ここらで終わり(ぉぃ