(i)MTBFを求めよ。
(ii)MTTRを求めよ。
(iii)アベイラビリティを求めよ。
信頼性計算は、伝送交換に比べると線路設備の方がちょびっとだけ難しいです。
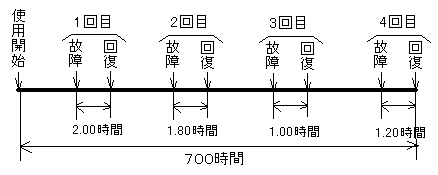
図は、通信線路の使用期間が700時間における故障の発生とさの修復時間を時系列に示したものである。

(i)MTBFを求めよ。
(ii)MTTRを求めよ。
(iii)アベイラビリティを求めよ。
(i)MTBFを求めよ。
MTBF(時間/件)
={700(時間)−(2.00+1.80+1.00+1.20)(時間)}/4(件)
=173.5(時間/件)
答え173.5(時間/件)
(ii)MTTRを求めよ。
MTTR(時間/件)
=(2.00+1.80+1.00+1.20)(時間)/4(件)
=1.5(時間/件)
答え1.5(時間/件)
(iii)アベイラビリティを求めよ。
アベイラビリティ
=MTBF/(MTBF+MTTR)
=173.5/(173.5+1.5)
=0.9914285
答え0.99
24時間連続運転しているある装置の300日間の故障件数は10[件]、故障修理に要した時間は200[時間]である。最後に発生した故障の修理完了時を300日間の終わりとする。
(i)MTBFを求めよ。
(ii)MTTRを求めよ。
(iii)アベイラビリティを求めよ。
(i)MTBFを求めよ。
装置を使用していた時間は24[時間]×300[日間]=7200[時間]
装置が稼働していた時間は、7200[時間]−200[時間]=7000[時間]
MTBF
=7000[時間]/10[件]
=700[時間/件]
答え700[時間/件]
(ii)MTTRを求めよ。
MTTR
=200[時間]/10[件]
=20[時間/件]
答え20[時間/件]
(iii)アベイラビリティを求めよ。
アベイラビリティ
=MTBF/(MTBF+MTTR)
=700/(700+20)
=0.9722
答え0.9722
ある装置の故障率が0.020(件/日)であるとき、
(i)装置の使用を開始してから10日間に対する信頼度R(10)を求めよ。
(ii)装置の使用を開始してから20日以内に故障する確率F(20)を求めよ。
(iii)装置の使用を開始してから100日間の間、信頼度を0.90以上に維持するためには、装置の故障率λ(件/日)を幾ら以下にしなければならないか。
(i)装置の使用を開始してから10日間に対する信頼度R(10)を求めよ。
信頼度R(10)
=e−λt
=e−0.020(件/日)×10(日)
=e−0.2
=0.8187
答え0.8187
(ii)装置の使用を開始してから20日以内に故障する確率F(20)を求めよ。
ここで言う故障率とは不信頼度の方の故障率です。
故障率=1−信頼度
故障率F(20)=1−信頼度R(20)
=1−e−λt
=1−e−0.020(件/日)×20(日)
=1−e−0.4
=1−0.670
=0.33
答え0.33
(iii)装置の使用を開始してから100日間の間、信頼度を0.90以上に維持するためには、装置の故障率λ(件/日)を幾ら以下にしなければならないか。
信頼度R>e−λt
0.90>e−λ(件/日)×100(日)
log0.90>−λ×100
−0.1053>−λ×100
λ>0.001053
答え0.001
図は、通信線路の使用時間が10,000時間における故障の発生とその修復時間及び予防保全の作業時間を時系列で示したものである。
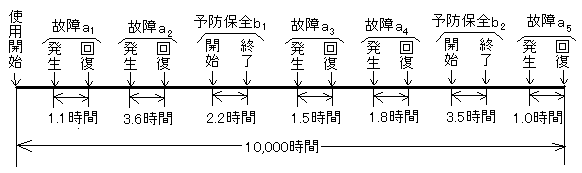
ただし、予防保全作業のうち、b1は通信線路を使用したまま行うことが出来る作業であり、b2は通信線路の使用停止が必要な作業である。
(i)通信線路のMDTは何時間か?
(ii)通信線路のMTTRは何時間か?
(iii)規定時間を3時間としたときの通信線路の保全度を、事後保全のみを対象として求めよ。
(i)通信線路のMDTは何時間か?
MDT
=(1.1+3.6+1.5+1.8+3.5+1.0)(時間)/6(件) 予防保全b2は線路を止めないと駄目なので使用不能時間に加算します。
=2.0833(時間/件)
答え2.0(時間/件)
(ii)通信線路のMTTRは何時間か?
MTTR
=(1.1+3.6+1.5+1.8+1.0)(時間)/5(件) MTTRは故障からの回復だけ考えます。
(iii)規定時間を3時間としたときの通信線路の保全度を、事後保全のみを対象として求めよ。
3時間以内に故障から回復しているのは、5件中4件なので、
保全度
=4/5
答え4/5
注 過去問には、80%と書いてあるのですが、別に4/5でいいと思います。どっちも同じ意味ですし。
次の文章は、通信線路の信頼度、MTBF等について述べたものである。空欄に最も適した語句を記せ。故障の発生は指数分布に従うものとする。
2地点A,B間に布設されている全長25[km]の通信線路があり、その1[km]当たりの故障率λは、8.0×10-4[件/年]である。この通信線路の全長のMTBFは、故障率λを用いて表すと
MTBF=(ア)[年]
となり、λの値を入れて算出すると(イ)[年]となる。
次に、この通信線路の全長の信頼度R25を故障率λと期間t[年]を用いて表すと
信頼度R25=exp(ウ)
となる。ここで通信線路の使用を開始してから(イ)年間に対するR25を算出すると、exp((エ))となる。
またR25が0.368となるまでの期間t[年]を算出すると、
0.368=exp((オ)×t)
loge0.368=(オ)×t
t=loge0.368/(オ)=−1/(オ)=(イ)[年]
となる。
(ア)について
1[km]当たりの故障率はλなので、25[km]の故障率は、25λ。
MTBF
=1/故障率
=1/25λ
答え1/25λ
(イ)について
1/25λのλの値は8.0×10-4(件/年)なので、計算すると
1/(25×8.0×10-4)
=50
答え50
(ウ)について
信頼度の公式はR=e−λtですが、λは1[km]あたりの故障率なので、25[km]の線路の故障率は25λです。
したがって、
R25=e−25λt
答え−25λt
(エ)について
R25
=exp(−25λt)
=exp(−25×8.0×10-4(件/年)×50(年))
=exp(−1)
答え−1
注 『98年版共通編電気通信主任技術者試験全問解答集』日本理工出版会 によると、(エ)の解答がlogee−λtになっているのですが、さっぱり意味が分かりません。
(オ)について
R25=e−25λt なので−25λのλに値を代入したものが答えです。
答え−0.02
復習
MTBF
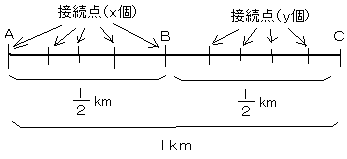
図は地点A〜B〜C間の通信線路を示したものである。A〜Bの通信線路は、1[km]当たりの故障率が2×10−4[件/年]、接続点1箇所当たりの故障率が4×10−3[件/年]であり、B〜C間の通信線路は、1[km]当たりの故障率が10−4[件/年]、接続点1箇所当たりの故障率が3×10−3件である。
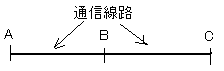
(i)A〜B間の距離を40[km]とするとき、A〜B間の通信線路のMTBFを10[年]以上とするためには、接続点の数を幾つ以下にしなければならないか。
(ii)A〜C間の距離がl[km]でA〜B間とB〜C間の距離が等しく、A〜B間の接続点の数をx、B〜C間の接続点の数をyとするとき、A〜C間の通信線路のMTBFを10[年]以上とするための条件を、l、x及びyを用いて表せ。ただしBの接続点はxに含まれるものとする。
(i)A〜B間の距離を40[km]とするとき、A〜B間の通信線路のMTBFを10[年]以上とするためには、接続点の数を幾つ以下にしなければならないか。
イメージ図は下のようになります。
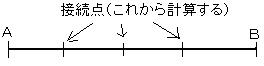
まず故障率の上限を求めます。
MTBF=1/λ
MTBF≧10[年/件]
1/λ≧10[年/件]
0.1≧λ[件/年]
A〜B間の通信線路の故障率は
2×10−4[件/年・km]×40[km]
=0.008[件/年]
A〜B間の接続点の故障率は、接続点の数をxとすると、
4×10−3[件/年・個]×y[個]
=4×x×10−3[件/年]
したがって、
0.1≧λ[件/年]
0.1≧0.008[件/年]+4×x×10−3[件/年]
x≦23
答え23箇所以下
注 通信線路の故障率と接続点の故障率を足して計算する理由については指数関数についてをどうぞ。
(ii)A〜C間の距離がl[km]でA〜B間とB〜C間の距離が等しく、A〜B間の接続点の数をx、B〜C間の接続点の数をyとするとき、A〜C間の通信線路のMTBFを10[年]以上とするための条件を、l、x及びyを用いて表せ。ただしBの接続点はxに含まれるものとする。
イメージ図は下のようになります。
まず故障率の上限を求めます。
MTBF=1/λ
MTBF≧10[年/件]
1/λ≧10[年/件]
0.1≧λ[件/年]
A〜B間の通信線路の故障率は距離がl/2[km]なので
2×10−4[件/年・km]×l/2[km]
=2×(l/2)×10−4[件/年]
B〜C間の通信線路の故障率は同様にして
10−4[件/年・km]×l/2[km]
=(l/2)×10−4[件/年]
A〜B間の接続点の故障率は、接続点の数がxなので、
4×10−3[件/年・個]×x[個]
=4×x×10−3[件/年]
B〜C間の接続点の故障率は、接続点の数がyなので、
3×10−3[件/年・個]×x[個]
=3×y×10−3[件/年]
したがって、
0.1≧λ[件/年]
0.1≧2×(l/2)×10−4+(l/2)×10−4+4×x×10−3+3×y×10−3
1000≧1.5l+40x+30x
答え1000≧1.5l+40x+30x
海底中継器が100台、システム長が12,000[km]の光海底ケーブルシステムがある。故障は、中継器のみに発生するものとし、いずれかの中継器が故障した場合でも、このシステムは機能を失う。
(i) システムの耐用寿命を25年とするとき、この期間における故障の発生を4件に抑えるためには、中継器1台あたりの故障率λを何FIT以下にしなければならないか。
(ii) いずれかの中継器の故障が5年間に1件発生するものとして、このシステムのアベイラビリティを求めよ。ただし、故障復旧の平均所要日数は、ケーブルシップ出港まで1日、出港から到着まで3日、現場到着から故障修理及び回復の確認試験に6日を要するものとする。
(i) システムの耐用寿命を25年とするとき、この期間における故障の発生を4件に抑えるためには、中継器1台あたりの故障率λを何FIT以下にしなければならないか。
システム全体の故障率[件/時間]
=4[件]/25[年]
=4[件]/(25×365[日]×24[時間])
=1.826×10−5
したがって、中継器一個の故障率は
1.826×10−5/100
=1.826×10−7
1FITは10−9なので、182.6FIT
答え182.6FIT
(ii) いずれかの中継器の故障が5年間に1件発生するものとして、このシステムのアベイラビリティを求めよ。ただし、故障復旧の平均所要日数は、ケーブルシップ出港まで1日、出港から到着まで3日、現場到着から故障修理及び回復の確認試験に6日を要するものとする。
修理に要する時間は、1+3+6=10日、で故障は1[件]なので、MTTRは10[日/件]。
MTBFは5[年]×365[日]−10[日](修理中なので稼働していない時間)=1815[日/件]。
アベイラビリティ
=MTBF/(MTBF+MTTR)
=1815/(1815+10)
=0.9945
答え0.9945
注 『98年版共通編電気通信主任技術者試験全問解答集』日本理工出版会 によると、MTBFが5×365になっているのですが、修理時間の10日を引かないと駄目だと思います。まー、計算すると誤差の範囲で解答は一緒になっちゃいますが。
電柱から加入者住宅への配線に用いられている引き込み線は、一般に、故障すると取り替え(張り替え)修理をしている。引き込み線の故障率は0.1[件/年]とするとき、
(i)引き込み線のMTTFは何年であるか。
(ii)引き込み線を設置してから4年後の信頼度Rを求めよ。
(iii)引き込み線の信頼度が0.8になるまでの期間tを求めよ。
ただし引き込み線の故障は偶発的に発生するものとする。
(i)引き込み線のMTTFは何年であるか。
MTTFは非修理系のMTBFです。したがって、
MTTF[年/件]
=1/λ[件/年]
=1/0.1
=10[年/件]
答え10[年/件]
(ii)引き込み線を設置してから4年後の信頼度Rを求めよ。
R
=e−λt
=e−0.1[件/年]×4[年]
=e−0.4
=0.6703
答え0.6703
(iii)引き込み線の信頼度が0.8になるまでの期間tを求めよ。
R=e−λt
0.8=e−0.1[件/年]×t[年]
log0.8=−0.1×t
−0.22314=−0.1t
t=2.231
答え2.231[年]
復習
MTTR
2地点間に布設された通信線路の故障率λが8×10−4[件/時間]であるとき、通信線路のアベイラビリティを99.2[%]以上とするためには、MTTRを何時間以下にしなければならないか。故障は偶発的に発生するものとする。
まずMTBFを求めます。
MTBF
=1/λ
=1/8×10−4
=1250[時間/件]
アベイラビリティ≧MTBF/(MTBF+MTTR)
0.992≧1250/(1250+MTTR)
MTTR≦10.08064516
答え だいたい10.08以下
復習
信頼度
システムの信頼度の向上を図るため、1ルート当たりの故障率λが4×10−5[件/時間]である通信線路が2地点間に冗長構成で布設されている。
システムの保全作業を伴わないものとして、使用を開始してから10,000時間後の2地点間のシステムの信頼度Rを0.99以上とするために必要なルート数nを求めよ。故障は偶発的に発生するものとし、通信線路以外には故障は無く、2地点間のいずれか1つのルートが正常であればこのシステムは正常に機能するものとする。
まず1ルートの信頼度を求めます。
信頼度
=e−λt
=exp(−4×10−5[件/時間]×10,000[時間])
=exp(−0.4)
=0.67
イメージ図は下のようになります。
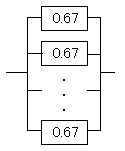
その0.67の箱がいくつあれば、0.99になるかを調べます。
これは並列モデルなので、
0.99≧1−(1−0.67)n
0.01≧(0.33)n
あとは0.01より小さくなるようなnを探します。
0.331=0.33
0.332=0.1089
0.333=0.035937
0.334=0.01185921
0.335=0.003913539
答え5ルート