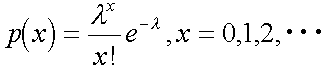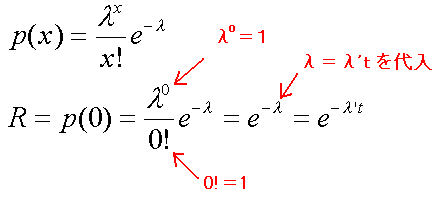2001年8月9日
信頼性計算のための数学
ここでは、信頼性計算のために必要な数学の知識を記しておきます。
いずれも高校程度の数学の知識です。
わかりにくいです(爆
- 指数関数について
- 対数関数について
- eとポアソン分布について
指数関数には以下の性質があります。
aman=am+n
故障率がλ1であるサブシステムAと、故障率がλ2であるサブシステムBとを直列に接続したシステムの故障率はいくらか?
解法
イメージ図にすると、こんな感じになります。
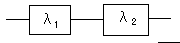
なんとなく信頼度計算の直列モデルに見えるので、λ1λ2とやってしまいそうですが、それは駄目です。
故障率の単位は(件/時間)ですが、λ1λ2の単位は(件/時間)2となりわけがわかりません。
直列モデルというのは信頼度の計算にのみ使って良いものです。そこで故障率を信頼度になおしてみます。
信頼度R=e−λt −−− (1)
ですので、上のイメージ図を信頼度になおすと以下のようになります。
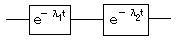
信頼度になおしたので直列モデルとして計算してよいです。
R=exp(−λ1t)×exp(−λ2t)
=exp(−λ1t)exp(−λ2t) ここで aman=am+n を使います。
=exp(−λ1t−λ2t)
=exp(−(λ1+λ2)t) −−− (2)
(1)と(2)比べてみると。
λ=λ1+λ2
となってます。
つまり、

のモデルの故障率は、λ1+λ2になるということです。
ちなみに、この問題、与えられているのが故障率(件/時間)で求めるのも(件/時間)で故障率です。そんなわけで、単位が同じなのだから、足すか引くかぐらいしかすることはありません。んで、引くのはおかしいだろうから足し算か・・・というように判断します。私の場合。
逆のことも考えてみます。
システム全体の故障率がλでそのシステムは同じ部品A100個で構成されていたとします。部品Aの故障率は?と聞かれましたら、それはもちろんλ/100です。
loge(e−λt)
=−λt
です。なんででしょうか?
指数関数と対数関数は逆関数の関係にあります。逆関数というのは、y=xを軸にして線対称な関数のことをいいます。
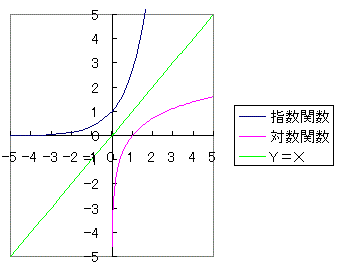
たとえば、y=2x と y=(1/2)xは逆関数の関係です(わかんなかったら自分で書いて下さい)。
逆関数には次の性質があります。
係数同士をかけると1になる。
y=2x と y=(1/2)xの係数はそれぞれ2と1/2ですが、これをかけると1になります。
対数関数と指数関数の係数ってなんでしょうか? それは、それぞれlogとeです。
係数をかけると1になってしまうのですから、
loge(e−λt)
=loge(exp(−λt))
=(loge)×(exp)×(−λt)
=−λt
となります。あー、ごまかして説明してますね、勘弁して下さい(爆 私は数学屋じゃないので。
っていうかeって何?
信頼性計算にはeという文字が出てきますが、このeっていうのはなんでしょうか?
このeの定義をちゃんとした数学でやると、大変です。っていうかさっぱりわかりません。そんなわけで、適当に説明します。(ぉぃ
eというのは円周率πと同じ無理数(小数点が無限に続いてかつ小数点より下の桁に繰り返しがない数、ホントはもっとちゃんとした定義が・・・)です。e=2.718281828459045・・・です。では2.7186という数字はどのように導くことが出来るのかを説明します。
途中をはしょって、いろいろやっていると(1+h)1/hという式が出てきます。この式のhを0に限りなく近づけます。これを数学の式ではlimh→0(1+h)1/hと書きます。
それでは、実際に(1+h)1/hのhを限りなく0に近づけてみましょう。
| h | (1+h)1/h |
|---|
| 1 | 2 |
| 0.1 | 2.59374・・・ |
| 0.01 | 2.70481・・・ |
| 0.001 | 2.71692・・・ |
| 0.0001 | 2.71814・・・ |
このように0.000000・・・001と限りなくhが0に近づいていくと2.718281828459045・・・になります。これを昔の人がeと定義したわけです。で、eの導出なんてどうでもよく(みなさん電子レンジの仕組みを知らなくても電子レンジを使えますよね)、eってのを定義すると何がうれしいのか、の方が我々には重要です。そこで、次にeの使用例について説明します。
eの完璧な定義が知りたかったら、微分積分学なんていう大学の数学科が使うような本を読めばもしかしたら分かるかもしれません(ぉぃ 上で書いた(1+h)1/hからeを導出する方法は大学の数学の先生に言わせると嘘です。
eを使うと何がうれしいのか?
eの重要な性質の以下のものがあります。
何回微分しても自分自身になる
(ex)'=ex
上の式の意味は「exは何回微分してもex」ということです。何回微分しても自分自身なのですから何回積分しても自分自身です。何回も微分できるのはうれしいらしいです。式を使って何か結果を出そうとするとき、微分や積分を使いますので微分や積分しやすいということはうれしいことです。
ポアソン分布や指数分布を表すのに必要
ポアソン分布というのは、フランスの数学者が考えた平均λ、分散もλ(重要)である確率分布のことを言います。ボアソン分布は、起こることが頻繁ではない事象の一定時間内の生起回数の確率分布として用いられます。信頼性計算では一定時間内に機器が故障する(または故障しない)確率を調べるために使います。
ボアソン分布の確率変数xの確率関数は以下のようになっています。
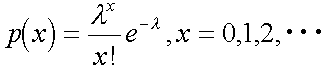
確率変数や確率関数の意味はほっといて、実際の信頼性計算ではこの式をどうやって使っているかを説明します。
例
故障率が0.2件/年のシステムがあります。このシステムの2年間の信頼度を求めなさい。
R=e−λ’t=e−0.2×2=0.670
答え0.67
上のような例題があります。p(x)=の式のλと区別するためλ’としています。いつもRで示されているのは、ポアソン分布の式ではp(x)にあたります。p(x)というのは「確率」のことです。信頼度Rというのはある時間内に機器が動いている確率のことを言いますので当たり前と言えば当たり前です。
機器がt年間に故障する回数はポアソン分布に従います。1年間に故障する回数の平均をλ’とするとt年間に故障する回数の平均はλ’tであるから、t年間に機器が1回も故障しない確率は、ポアソン分布の平均λにあたる数はλ’tになります。ボアソン分布の式のp(x)の中にあるxは確率変数といいます。確率というのは何か値が決まると決まる数字ですが、その「何か値」が確率変数です。わかりにくいので例を。。例えばサイコロで1が出る確率は1/6ですが、1/6がp(x)(確率)で、1がx(確率変数)です。1という値が決まると、その確率は1/6と分かります(ちなみにサイコロの出る目はポアソン分布には従わないので上のp(x)=の式のxに1を代入してもp(x)は1/6にならないです。)。信頼性計算では「機器が0回故障する確率(要するに機器が故障しない確率)」が知りたいので、p(x)のxは0になります(ちなみに1回故障する確率が知りたかったらxは1、2回だったらxは2になります)。そこでp(x)=の式のxに0を代入してみると
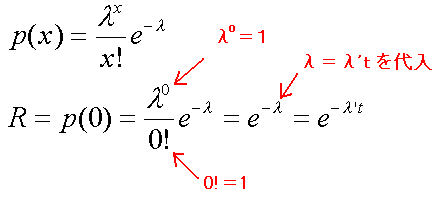
めでたくいつも使うR=e−λtが出てきます。