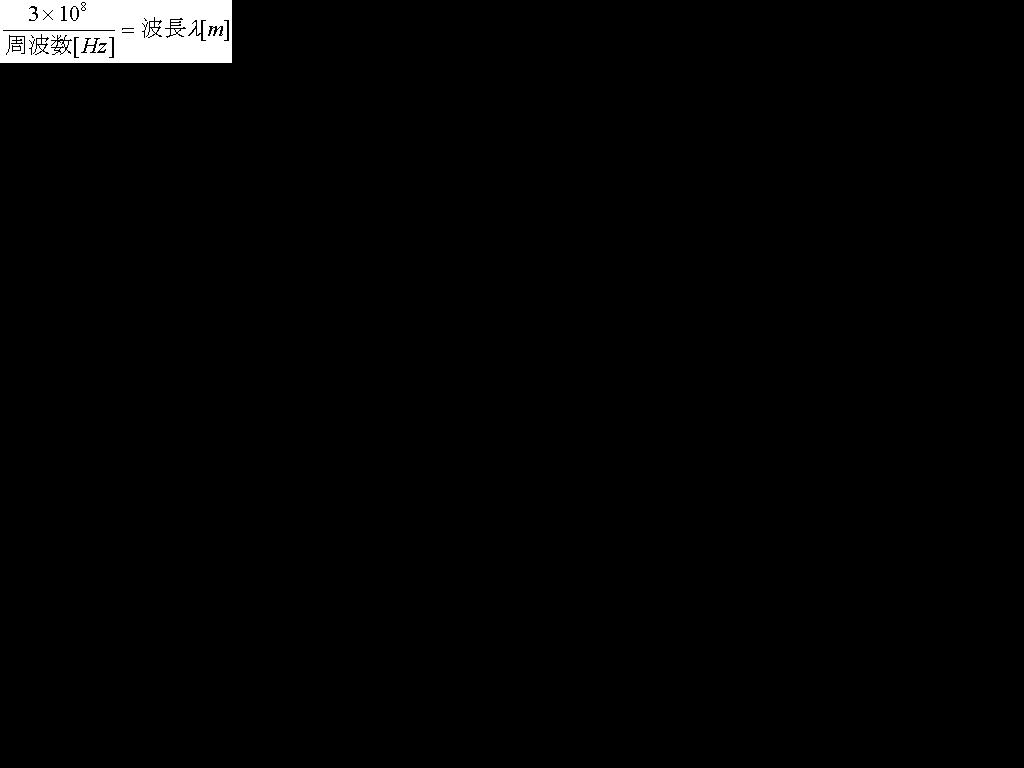
例えば3[GHz]の電波の波長はいくらかといった場合は、3×108/3×109=0.1[m]となります。
A-1 記述は、アンテナの放射抵抗について述べたものである。□内に入れるべき正しい字句の組合せを下の番号から選べ。ただし、アンテナの損失は無いものとする。
(1) アンテナの給電点電流I[A]を流すと、電波の放射により電力Pr[W]を消費する。これは、抵抗Rr[Ω]によって電力Prが消費されたことと等価であり、次式の関係が成り立つ。
Pr=□A [W]
(2) Rrは、□B抵抗であり、これを放射抵抗といい、次式によって表される。
Rr=□C [Ω]
| A | B | C | |
|---|---|---|---|
| 1 | | I |2Rr | 実在する | Pr/| I | |
| 2 | | I |Rr | 仮想的な | Pr/| I | |
| 3 | | I |2Rr | 仮想的な | Pr/| I |2 |
| 4 | | I |Rr | 仮想的な | Pr/| I |2 |
| 5 | | I |2Rr | 実在する | Pr/| I |2 |
まず□Aですが、オームの法則を知っていれば間違えることはありません。
オームの法則はE=RI(E[V]、R[Ω]、I[A])です。そして、P=EI(P[W}、E[V]、I[A])です。したがって、P=I2Rです。よって□Aは| I |2Rrです。
次に□Cです。□AでPr=| I |2Rrと分かりました。□Cはこの式を変形してRr=を知りたいだです。したがって、□CはPr/| I |2です。
最後に□Bですが、普通に考えれば「放射抵抗」なんてものが実際の抵抗としてあるわけないので仮想的なことは分かります。
問題文中に「抵抗Rr[Ω]によって電力Prが消費されたことと等価であり」とありますが、「等価」といっていることからも抵抗が仮想的だと分かります。したがって答えは3です。
A-2 自由空間に置かれた微小電気ダイポールから放射される放射電界の強度は、微小電気ダイポールからの距離をd[m]、波数(位相定数)をβ[rad/m]とすると、β2/dに比例し、また、誘導電界の強度は、β/d2に比例する。放射電界と誘導電界の強度が等しくなる距離の値として、最も近いものを下の番号から選べ。ただし、周波数は100[MHz]とする。
1 0.5[m]
2 1[m]
3 2[m]
4 4[m]
5 8[m]
ラジアンと周波数から波長を求める術を知っていればとけますが、知らないとお手上げです。
まず、放射電界の強度がβ2/dで誘導電界の強度がβ/d2で、放射電界の強度と誘導電界の強度が等しいところを知りたいと言っているのですから、β2/d=β/d2という式を解けばいいことは分かります。
この式を簡単にすると、β=1/dなので、d=1/βです。βが分かればdも分かります。
位相定数β
β=2π/λ
この公式はよく使うのでぜひ覚えておいて頂きたいです。
けど、公式を知らなくても位相定数βの単位を見ればおのずと位相定数の公式は分かります。
βの単位は[rad/m]です。ラジアンをメートルで割ってあげればいいわけです。100[MHz]の電波の波長は
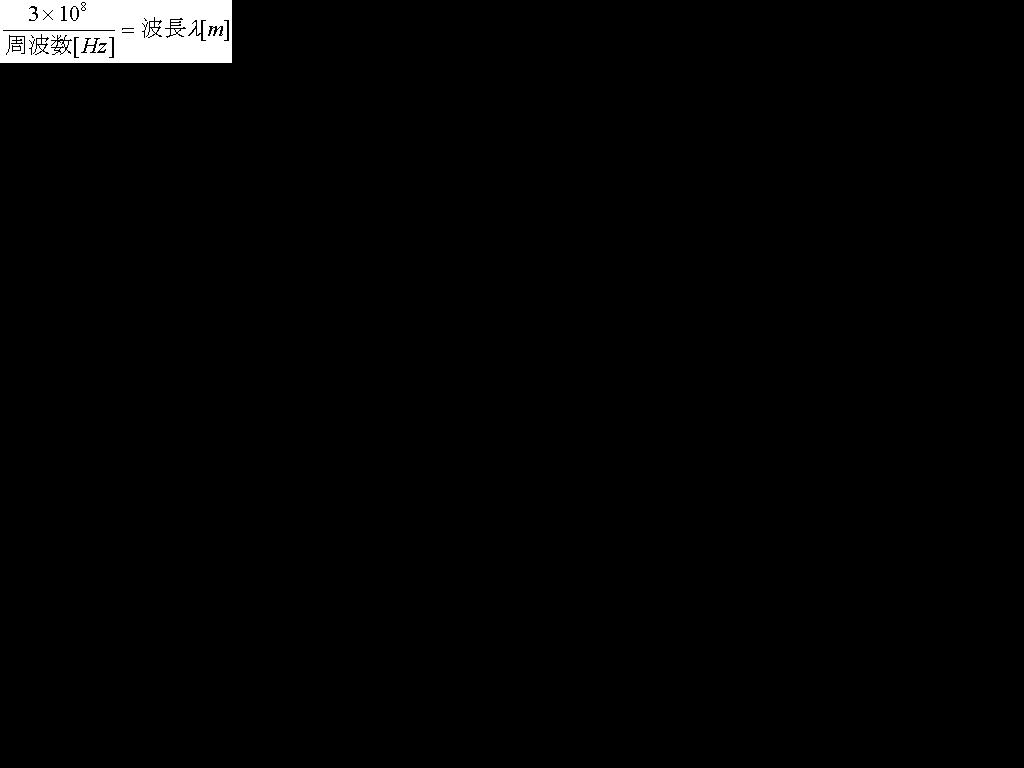
例えば3[GHz]の電波の波長はいくらかといった場合は、3×108/3×109=0.1[m]となります。
より、3×108/100×106=3[m]です。そして、1波長は2π[rad]です。2π[rad]で3[m]でβは[rad/m]なのでラジアンをメートルで割ってあげればいいので、βは2π/3=2.1[rad/m]。d=1/βなので、1/2.1=0.5。答えは0.5です。
A-3 次の記述は、アンテナを絶対利得、相対利得及び指向性利得で表したときのそれぞれの関係について述べたものである。このうち誤っているものを下の番号から選べ。
1 相対利得は、絶対利得より小さい。
2 指向性利得は、相対利得より大きい。
3 アンテナの損失が無いとき、絶対利得と指向性利得は等しい。
4 アンテナの損失があるとき、相対利得が最も小さく、絶対利得が最も大きい。
5 アンテナの損失があるとき、指向性利得は絶対利得より大きい。
知らなければ出来ない問題ですが、よく出題されるので陸技を受けるならば知っておいて欲しい問題です。
何も知識がない場合でも2択に絞ることが可能です。
4番の選択肢は相対利得<指向性利得<絶対利得です。5番の選択肢は絶対利得<指向性利得です。したがって明らかに4と5は矛盾しているのでどちらかが間違いだと分かります。
指向性利得はあまり覚えてなくてもいいですが、絶対利得と相対利得は必ず覚えてください。
絶対利得とは等方性アンテナを基準とした任意のアンテナの利得です。
相対利得とは半波長ダイポールアンテナを基準とした任意のアンテナの利得です。
半波長ダイポールアンテナの絶対利得は1.64(2.15[dB])です。当たり前ですけど、半波長ダイポールアンテナの相対利得は0[dB]です。
指向性利得とはあるアンテナから電波が全方向へ均等に放射されたとしたときの放射強度に対する特定方向への放射強度の比です。
指向性利得×アンテナ効率(<1)=絶対利得

| 相対利得 | 絶対利得 | 指向性利得 | |
|---|---|---|---|
| 半波長ダイポールアンテナ | 0[dB] | 2.15[dB] | 2.15[dB] |
| 等方性アンテナ | -2.15[dB] | 0[dB] | 0[dB] |
| アンテナ効率が0.8で相対利得が10[dB]のアンテナ | 10[dB] | 12.15[dB] | 13.1[dB] |
上の解説より4が間違っています。
A-4 周波数30[MHz]で使用する半波長ダイポールアンテナの実効長として、最も近いものを下の番号から選べ。ただし、図に示すように、アンテナの中心Oを原点にとり、アンテナ素子の長さの方向をx[m]とし、アンテナの給電点電流をI0[A]及び波長をλ[m]としたとき、電流分布は次式で表される正弦状の分布とする。また、正弦状の電流分布の面積AGBに等しい面積CDFEを持ち、かつ、給電点電流が等しい一様な電流分布を考えたとき、長さEFを実効長le[m]という。
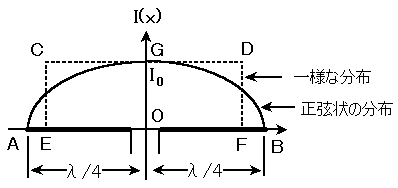
![]()
1 0.8[m]
2 1.6[m]
3 2.2[m]
4 2.8[m]
5 3.2[m]
実際に計算してもいいのですが、波長から半波長ダイポールアンテナの実効長を求める式は覚えておくべき公式の一つですので覚えておきましょう。確かアマチュア無線4級にも波長から半波長ダイポールアンテナの実効長を求める問題は出ています。
半波長ダイポールアンテナの実効長

le[m](アンテナの実効長) λ[m](波長)
λ[m]=300/f[MHz] ですので、λ=300/30=10[m]。
le[m]=λ[m]/π=10/3.14=3.18[m]。よって答えは5です。
A-5 次の記述は、図にしめす集中定数形バランについて述べたものである。□内に入れるべき正しい字句の組合せを下の番号から選べ。
(1) a端子とアースの間に□A回路を接続し、bc端子間に□B回路を接続して平衡ー不平衡の変換を行う。
(2) 一次回路及び二次回路を使用周波数に□C使用する。
(3) 一次コイルと二次コイルの相互インダクタンスM[H]、一次側及び二次側の特性インピーダンスをそれぞれZ1[Ω]、Z2[Ω]及び角周波数をω[rad/s]とすれば、整合条件はωM=□D[Ω]である。
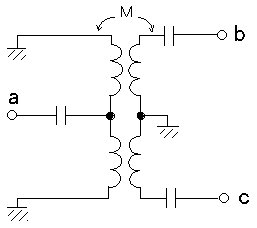
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 平衡 | 不平衡 | 同調させて | Z1Z2 |
| 2 | 不平衡 | 平衡 | 同調させて | |
| 3 | 平衡 | 不平衡 | 同調させないで | |
| 4 | 不平衡 | 平衡 | 同調させて | Z1Z2 |
| 5 | 平衡 | 不平衡 | 同調させないで | Z1Z2 |
まず何も知らなくても分かるのは□Dです。
□Dの単位は[Ω]です。Z1とZ2の単位は特性インピーダンスですので[Ω]です。したがって□DにZ1Z2を選んでしまうと単位が[Ω2]になってしまいますので明らかにおかしいです。したがって答えは2か3のどちらかにしぼれます。
次に分かりそうなのは□Cです。感覚的に「同調させて使う」のと「同調させないで」使うのでは「同調させて」使う方が正しい気がします。無線の問題の場合「同調させないで」使う回路ってのはないと思います。したがって答えは2です。
ちなみに、平衡線路と不平衡線路は無線の常識として覚えておくのがいいと思います。
平衡線路は昔のテレビによく繋いだ平行フィーダ線のことです。普通の電源コードを思い浮かべて頂ければいいと思います。線が2本ありますので電気は負荷の方に行って帰ってきます。
不平衡線路は同軸ケーブルです。最近のテレビに繋いでいる線はみんなこれです。電気は真ん中にある中心導体にしか通らないので行った電気は帰ってきません。
文章だと伝わりにくいので写真を提示します。

下の線が平行フィーダ線で上の線はおなじもの同軸ケーブルです。
問題の図に戻りましょう。
平行フィーダ線は線が2つありますので、問題の図の右側が平行フィーダ線になります。同軸ケーブルは線が1つかないので問題の図の左側が同軸ケーブルになります。
さて、ここで何も知らない方ですと「同軸ケーブルには外部導体があるから、中心導体と外部導体とで線は2つあるんじゃないですか?」と突っ込みたくなります。ええと、確かに外部導体はあるんですけど、この外部導体は中心導体を雑音から守るためのシールドとしてあるだけですので電気は流れません。シールドなので接地されています。いや・・・嘘言ってる気がするな・・・
A-6 終端にZr[Ω]の負荷が接続されている給電線の電圧反射係数Γ及び電圧定在波比Sを表す式の組み合わせとして、正しいものを下の番号から選べ。ただし、給電線の特性インピーダンスは、Z0[Ω]とする。
| Γ | S | |
|---|---|---|
| 1 | |Zr-Z0|/|Zr+Z0| | (1-|Γ|)/(1+|Γ|) |
| 2 | |Zr-Z0|/|Zr+Z0| | (1+|Γ|)/(1-|Γ|) |
| 3 | |Zr+Z0|/|Zr-Z0| | (1-|Γ|)/(1+|Γ|) |
| 4 | |Zr+Z0|/|Zr-Z0| | (1+|Γ|)/(1-|Γ|) |
| 5 | |Zr-Z0|/|Zr+Z0| | (1-|Γ|)/(1+|Γ|) |
知らなきゃ出来ない問題ですが、よく出るので公式を覚えてください。
電圧定在波比と反射係数の定義(まあ重要)

S[単位なし](電圧定在波比) Γ[単位なし](反射係数)
電圧定在波比と反射係数の相互変換(重要)

S[単位なし](電圧定在波比) Γ[単位なし](反射係数)
よって答えは2です。
A-7 次の記述は、方形導波管内を伝搬する電磁波について述べたものである。このうち誤っているものを下の番号から選べ。
1 一般に、基本モードが利用されている。
2 管内を伝搬する電磁エネルギーの速度は、自由空間の速度より遅い。
3 管内波長は、自由空間波長より長い。
4 遮断波長より長い波長の電磁波は、伝送されない。
5 遮断波長は、導波管の管軸方向の長さの寸法によって決まる。
知らなくてもなんとかなります。
5の文章によると、「遮断波長は、導波管の管軸方向の長さの寸法によって決まる。」となっていますが、導波管の長さで波長が決まってしまったら大変です。例えば、導波管が長い場合は波長が長くないと駄目ということでしたら、波長が短い場合は導波管の長さが限られてしまうことになります。伝送路10mが欲しい場合は「1mだけ導波管を使って、あと9mは同軸ケーブルで伝送する」というよくわからないことになってしまうので明らかに5は違います。
したがって答えは5です。
ちなみに1〜4までの特徴は覚えておきましょう。よく出ます。
ちなみに2の「管内を伝搬する電磁エネルギーの速度」のことを郡速度といいます。
また管内波長は普通λgで表します。
A-8 図に示す一次巻線に対する二次巻線の比nが2の変成器による整合回路において、一次側回路及び二次側回路のインピーダンスをそれぞれ純抵抗R1[Ω]及びR2[Ω]としたとき、整合がとれるR1及びR2の値の組合せとして、正しいものを下の番号から選べ。
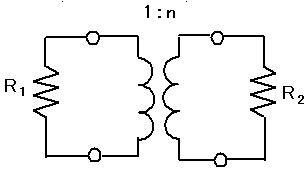
| R1 | R2 | |
|---|---|---|
| 1 | 50[Ω] | 75[Ω] |
| 2 | 100[Ω] | 142[Ω] |
| 3 | 142[Ω] | 100[Ω] |
| 4 | 150[Ω] | 300[Ω] |
| 5 | 200[Ω] | 800[Ω] |
電気回路の基本なので、これくらいは出来るようにしておきましょう。
1:2の変成器を通ると、電圧は2倍、電流は1/2になります。したがって、抵抗はR=E/Iなので、R=2/(1/2)=4。したがって抵抗は4倍必要です。答えは5です。
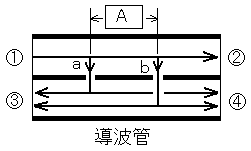
A-9 次の記述は、図に示す2結合孔方向性結合器について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。
(1) 二本の導波管を平行にして密着させ、それらの密着面に管内波長の□Aの間隔で二個の結合孔a及びbを開けたものである。
(2) ○1から入力された電磁波は、その一部が結合孔a及び結合孔bを通ってそれぞれ○3及び○4へ等分されて伝送される。このとき、○4へ向かう電磁波は、aを通る伝送距離とbを通る伝送距離が等しいので、同位相で加わり合い○4へ伝送される。また、○3へ向かう電磁波は、aを通る伝送距離とbを通る伝送距離との間に□Bの差があるので互いに打ち消しあう。同様にして、○2から入力された電磁波は、○3へ伝送□Cが、○4へは伝送□D。
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1/2波長 | 1/4波長 | されない | される |
| 2 | 1/2波長 | 1/2波長 | されない | される |
| 3 | 1/4波長 | 1/4波長 | される | されない |
| 4 | 1/4波長 | 1/2波長 | される | されない |
| 5 | 1/2波長 | 1/4波長 | される | されない |
180度位相がずれた波が重なると打ち消しあうという事実が分かっていればOKです。
まず□Bです。波が打ち消しあうためには、位相が180度ずれている(1/2波長ずれている)必要がありますので、□Bは1/2波長です。
次に□Aですが、○1→a→○3のルートと○1→b→○4のルートで位相が1/2波長ずれるためには、□Aは1/4波長である必要がありますよね。したがって、□Bは1/4波長です。ので、答えは4です。
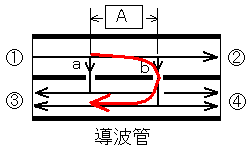
赤い矢印の距離が1/2λだと下の図のようになって波が打ち消しあいます。
A-10 利得がG(真値)のパラボラアンテナの実効面積Ae[m2]を表す式として、正しいものを下の番号から選べ。ただし、開口面の面積をA[m2]、波長をλ[m]、開口効率をηとしたとき、Gは次式で表されるものとする。
G=4πAη/λ2
1 Ae=Gλ/2π
2 Ae=Gλ2/4π
3 Ae=Gλ2/2π
4 Ae=G/4πλ
5 Ae=G/2πλ2
式をただ変形するだけという中学生でも出来るんじゃないかと思うような問題です。
G=4πAη/λ2 をA=の式に直してみると
A=Gλ2/4πη となります。解答選択肢でこれに一番近いのは2です。したがって答えは2です。
ちなみにこの問題はよく出るので式を暗記しておくべきでしょう。
アンテナの実効面積などなど(重要)

Ae[m2](アンテナの実効面積) A [m2](アンテナの面積) λ [m](波長) G [単位なし](利得) η[単位なし](開口効率)
A-11 次の記述は、2線式折り返し半波長ダイポールアンテナについて述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) 二本の半波長ダイポールアンテナを極めて接近して□Aに置き、それらの先端を互いに接続し、いずれか一方のアンテナの中央から給電する。
(2) 二本の半波長ダイポールアンテナの太さの比を変えると入力インピーダンスが変わる。太さが同じ(比が1対1)場合は、一本の場合のインピーダンスの□Bとなる。
(3) 指向性は、一本の半波長ダイポールアンテナの指向性と□C。
| A | B | C | |
|---|---|---|---|
| 1 | 直角 | 2倍 | 異なる |
| 2 | 平行 | 4倍 | 異なる |
| 3 | 平行 | 2倍 | 同じである |
| 4 | 平行 | 4倍 | 同じである |
| 5 | 直角 | 2倍 | 同じである |
知らなきゃ分からない問題ですが、□Aは常識で分かりますので3択まではもっていけます。後は運です。
□Aは、直角にダイポールアンテナを置いて、その先端を繋ぐ姿を想像するとかなり滑稽です。2線式折り返しなのですから平行に置いてあるのが妥当でしょう。したがって□Aは平行です。
折り返し半波長ダイポールアンテナの特徴はよく出る気がしますので、□Bと□Cは覚えておいておいた方がよいです。入力インピーダンスは4倍。指向性は半波長ダイポールアンテナと同じです。
A-12 次の記述は、航空機で使用する距離測定装置(DME)用アンテナについて述べたものである。□内に入るべき字句の正しい組合せを下の番号から選べ。
DMEは、航空機が地上DME施設の基準点までの傾斜距離を測定するたるの二次元レーダー装置であり、航空機に搭載されたインタロゲータ(質問器)と地上に置かれたトランスポンダ(応答器)で構成されている。
(1) 航行中の航空機は、搭載しているインタロゲータから地上に設置されているトランスポンダへ質問信号を送り、その応答信号を受信して電波の往復時間から傾斜距離を求める。このため、航空機のインタロゲータ用アンテナは□Aである。
(2) 地上に設置されているトランスポンダ用のアンテナは、垂直ダイポールアンテナを10段程度配置し、□B偏波の電波を放射する。このアンテナは、大地反射波を抑えるために水平面から□Cへの放射が殆どない。
| A | B | C | |
|---|---|---|---|
| 1 | 無指向性 | 垂直 | 下方 |
| 2 | 無指向性 | 水平 | 上方 |
| 3 | ペンシルビーム指向性 | 垂直 | 上方 |
| 4 | ペンシルビーム指向性 | 水平 | 上方 |
| 5 | ペンシルビーム指向性 | 垂直 | 下方 |
航空レーダーの問題かよー、と思ってしまいますが、とりあえず二択までには簡単に絞れます。
まず□Bですが、「垂直ダイポールアンテナ」から水平偏波をだすわけないので、□Bは垂直です。
次に□Cですが、大地反射波が来て欲しくないのですから大地の方に電波を飛ばさなければいいです。したがって□Cは下方です。これで1か5に絞れます。
□Aですが、まず「ペンシルビーム指向性というのは、その名前から多分指向性が鋭いんだろうな」と予想します。そして「飛行機はとても早く飛んでいるので、トランスポンダ用のアンテナにねらいを定めてペンシルビームを打つのは難しいんじゃないか」と考えますので、□Aは無指向性です。したがって答えは1です。
A-13 次の記述はホーンレフレクタアンテナについて述べたものである。このうち誤っているものを下の番号から選べ。
1 電磁ホーンとその近傍におかれた一枚の反射鏡から構成されている。
2 反射鏡は、通常、回転放物面の一部が用いられる。
3 電磁ホーンの開口面と回転放物面反射鏡の焦点は一致している。
4 電磁ホーンからアンテナの開口面までの伝送路中には、反射鏡以外に電波を反射又は散乱させるものは無い。
5 使用する電磁ホーンの形により、円すいホーンレフレクタアンテナや角すいホーンレフレクタアンテナなどがある。
ホーンレフレクタアンテナはよく出てくるので形くらいは頭の中にイメージとして残しておくべきでしょう。その姿は参考書を見てください。
ホーンレフレクタアンテナを知らなくても日本語を読めば答えを絞り込めます。
2と3を読むと「回転放物面」という言葉が出てきますので、回転放物面をもつ反射鏡がないと、2と3が誤りになってしまうので、ホーンレフレクタアンテナには回転放物面を持つ反射鏡があると分かります。したがって2は正解です。
次に1と4です。4を読むと「電磁ホーンからアンテナの開口面までの伝送路中には、反射鏡以外に電波を反射又は散乱させるものは無い」ので、4を読む限りでは反射鏡は1枚です。そして、1は反射鏡が1枚と言っています。したがって、反射鏡が1枚でないと矛盾が生じます。また、1では「電磁ホーンと反射鏡から構成されている」と書いてあり4では「伝送路中には電磁ホーンと反射鏡以外はない」と言っているので、ホーンレフレクタアンテナは「電磁ホーンと反射鏡から構成されている」のは正しそうです。したがって、1と4は正解です。
誤っている候補は3か5です。
ちなみにパラボラアンテナの形を知っていればパラボラアンテナの絵を書くと3はパラホベラアンテナの性質と分かります。
答えは3です。
ちなみに、電磁ホーンでよく出題されるのは「ホーンの開き角度が一定の場合はホーンの長さを増すと指向性がするどくなって利得があがる」「ホーンの長さが一定の場合は開き角に最適な角度が存在する」という2つの性質です。覚えておきましょう。
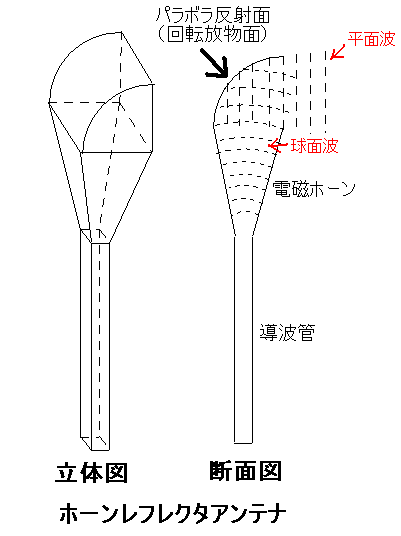
サイドローブが小さい。開口効率が大きい。直線偏波、円偏波に使用できる。
A-14 次の記述は、中緯度地域のスポラジックE層について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) E層とほぼ同程度の高さに、突発的に現れる層の厚さが□A電離層であり、その電子密度は、時間とともに大きく変動する。
(2) 発生時期は、地域によって異なり、日本などの中緯度地域では夏季の□Bに多く発生する。
(3) スポラジックE層が発生すると、□C帯の低い周波数の電波が反射され、1000〜2000キロメートルの遠方まで伝播することがある。
| A | B | C | |
|---|---|---|---|
| 1 | 厚い | 夜間 | UHF |
| 2 | 薄い | 夜間 | VHF |
| 3 | 薄い | 日中 | VHF |
| 4 | 薄い | 日中 | UHF |
| 5 | 厚い | 日中 | UHF |
スポラジックE層はアマチュア無線の試験では当たり前の話なんですが、いきなり陸技試験だと、聞いたことがないかもしれないです。
まず分かるのは□Cです。「□C帯の低い周波数の電波」となっていて選択肢がVHFとUHFなので周波数の低いVHFを選ぶのが妥当です。次に□Bですが、夏季に発生するってことは暑いとか太陽の影響かなと予想できるので日中と夜間を選ぶなら日中でしょう。したがって答えは3です。
参考書によると短波(HF帯)に妨害を与えるとあるんですけど、確かスポラジックE層のおかげですげぇ電波が飛ぶこともあったようななかったような気が・・・
高さは100km。夏に出る。黒点の影響は受けない。超短波をよく反射。
ちなみに、電離層は下からD層、E層、F層の順番です。
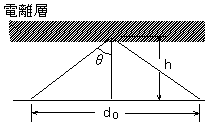 A-15 電離層の臨界周波数が4[MHz]で見掛けの高さが300[km]のとき、周波数5[MHz]の電波の跳躍距離の値として、正しいものを下の番号から選べ。ただし、大地は水平な平面であり、電離層は大地に平行であるものとする。図は、電離層の見掛けの高さがh[m]であり、電離層への電波の入射角がθ度のとき、電離層反射波が届く地表距離d0[m]を示したものである。また、臨界周波数fc[Hz]と周波数f0[Hz]との間には、次式の関係があるものとする。
A-15 電離層の臨界周波数が4[MHz]で見掛けの高さが300[km]のとき、周波数5[MHz]の電波の跳躍距離の値として、正しいものを下の番号から選べ。ただし、大地は水平な平面であり、電離層は大地に平行であるものとする。図は、電離層の見掛けの高さがh[m]であり、電離層への電波の入射角がθ度のとき、電離層反射波が届く地表距離d0[m]を示したものである。また、臨界周波数fc[Hz]と周波数f0[Hz]との間には、次式の関係があるものとする。
f0=fcsecθ
1 450[km]
2 600[km]
3 900[km]
4 1200[km]
5 1800[km]
中学生や小学生に数学、算数を教えていると3とか4とか5という数字が出てくると「3:4:5の三角形の可能性」を真っ先に思いつくのですが、この問題も3とか4とか5という数字が出てきますので、多分「3:4:5」の三角形だろうと予想をします。予想するだけですよ。ちなみにこの問題は「どうせ3:4:5の三角形だろ」と思えば、臨界周波数もsecも知らなくても勘で解けます。私はそうやって解きました。あとで一応確かめますけど。
臨界周波数の問題はよく出題されるので覚えておくべきでしょう。
この問題は臨界周波数の概念を知っていて、secを知っていれば解けます。secθ=1/cosθです。類似品にcosecθ=1/sinθがあります。陸技の試験ではsecθしか出てきませんので、secθ=1/cosθを覚えておいてください。
f0=fcsecθ
f0cosθ=fc
5cosθ=4
cosθ=4/5
というわけで、
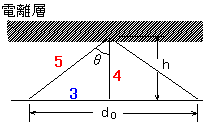
となります。赤い数字はcosθ=4/5から分かる事実。青い数字は斜辺が5、もう一つの辺が4なので「3:4:5」の三角形ということが判明した時に分かる事実です。ここらへんがさっぱり分からない方は、三角関数の初歩のsinθとcosθの公式を読んでください。
これが分からなかったら、大地から電離層に向かっている直線は臨界周波数と同じで4、飛ばす電波の周波数は三角形の斜辺で5、あとは三平方の定理から残りの辺は3、と覚えちゃった方が早いです。
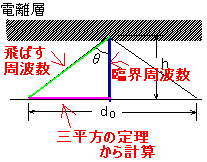
hは300[km]ですので
4:300[km]=3:x[km]
x=225[km]
これはd0の半分なので、2倍して450[km]。
A-16 次の記述は、マイクロ波の見通し内伝搬におけるフェージングについて述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) 伝搬路の中にラジオダクトが発生したとき、□Aが時間とともに変動するとフェージングが発生する。
(2) 温帯地方では、□Bより□Cの方が、また、風雨の日よりも晴天でおだやかな日の方が一般にフェージングの発生が多い。
(3) 山岳回線よりも海上や沿岸回線の方がフェージングの発生が□D。
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 伝送曲線 | 冬季 | 夏季 | 多い |
| 2 | M曲線 | 冬季 | 夏季 | 多い |
| 3 | 伝送曲線 | 夏季 | 冬季 | 多い |
| 4 | M曲線 | 夏季 | 冬季 | 少ない |
| 5 | 伝送曲線 | 夏季 | 冬季 | 少ない |
一陸特を受けたことがあったり一アマとか二アマを受けていると当然知ってる事実の問題なんですが、陸技だとあんまり出ない気がする問題なので陸技試験が無線の試験でははじめてです〜な感じだとつらいです。
まず、陸技試験では「伝送曲線」という言葉は忘れていいです。曲線はM曲線だけ覚えてください。私はこの問題を読むまで伝送曲線を知りませんでした。
次に、電波伝搬で覚えるキーワードは「夏」です。「夏」の方が活発と覚えてください。夏の方がなんか活発そうですよね。
そんなわけで□AはM曲線です。□Bは夏季、□Cは冬季です。
□Dはそういうものらしいです。私なら「山は山岳回折とかで利得が増えたりするから、やっぱ海が近いほうが大変そうだ」とか「海の方がなんか風とか水とかで大気が不安定そうだから、フェージングでるかも」とか覚えます。
A-17 図に示すように、送受信点間の地表距離dが10,000[m]の平面大地上の伝搬において、地上高h1が30[m]のA地点から地上高h2が10[m]のB点に至る直接波の伝搬通路長r1と大地反射波の伝搬通路長r2との通路差による電波の位相差として、最も近いものを下の番号から選べ。ただし、周波数を100[MHz]とし、h1>>d及びh2>>dとする。また、r1及びr2は、次式で与えられるものとする。
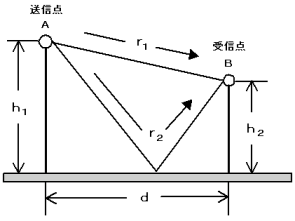
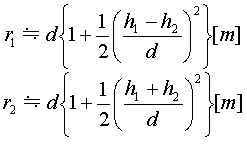
1 0.02[rad]
2 0.09[rad]
3 0.13[rad]
4 0.18[rad]
5 0.26[rad]
位相差の意味とradを知っていれば、式に代入するだけで解けるお手軽問題です。
radに関しては角度とラジアンを、位相に関しては位相をご覧下さい。
「通路差による電波の位相差」を知りたいのでまず通路差を求めます。通路差はr1とr2の差です。dに10,000[m]、h1に30[m]、h2に10[m]を代入して計算するとr1=10000.02[m]、r2=100000.08[m]。通路差[m]=r2-r1=0.06[m]。ところで周波数が100[MHz]の電波の波長は300/100=3[m]です(波長と周波数の換算)。ということは3[m]で2πです。通路差は0.06[m]です。したがって、
3[m] : 2π[rad] = 0.06[m] : x[rad]
x = 0.125[m]
従って答えは3です。
ちょっと補足します。r2の道をたどってきた電波はr1よりもちょっと長い道のりをたどってきます。そのため、受信点Bではr1の電波がたどり着いてからちょっと経った後にr2の電波を受信します。要するに電波がちょっとずれて到着するわけです。この時の電波のずれ(位相の差)が知りたいな〜というのがこの問題です。
A-18 次の記述は図に示すマジックTを用いたインピーダンスを測定する方法について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。また、測定器相互間の整合はとれているものとし、接続部からの反射は無視できるものとする。
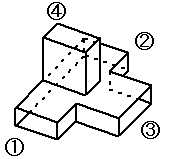 (1) 図において、○1及び○2に任意のインピーダンスを接続して○3からマイクロ波を入力すると、等分されて○1及び○2へ進むが、反射波があると○4へ出力される。その大きさは、○1及び○2からの反射波の□Aである。
(1) 図において、○1及び○2に任意のインピーダンスを接続して○3からマイクロ波を入力すると、等分されて○1及び○2へ進むが、反射波があると○4へ出力される。その大きさは、○1及び○2からの反射波の□Aである。
(2) 未知のインピーダンスを測定するには、○1に標準可変インピーダンス、○2に被測定インピーダンス、○3に高周波発信器及び○4に□Bを接続し、標準可変インピーダンスを加減して□Bへの出力が□Cになるようにする。このときの標準可変インピーダンスの値が被測定インピーダンスの値である。
| A | B | C | |
|---|---|---|---|
| 1 | 差 | 検出器 | 最小 |
| 2 | 和 | 終端抵抗 | 最小 |
| 3 | 差 | 終端抵抗 | 最大 |
| 4 | 和 | 終端抵抗 | 最大 |
| 5 | 差 | 検出器 | 最大 |
 マジックTはよく出題される気がするので、その仕組みを覚えておいて損はないでしょう。マジックTに関してはこちらを参照ください。
マジックTはよく出題される気がするので、その仕組みを覚えておいて損はないでしょう。マジックTに関してはこちらを参照ください。
まず□Aです。この問題はマジックTの図をよく覚えてないと出来ない嫌な問題です。私は間違えました。
○3から入った波は等分されて○1と○2に入ります。でも、○1と○2には任意のインピーダンスが接続されています。マジックTのインピーダンスとは違うインピーダンスが接続されています。したがって、マジックTと任意のインピーダンスとの境目でインピーダンスが違うため(不整合のため)に反射がおきます。すると○1と○2からマジックTに電波が帰っていきます。この電波はどっちも○4に出力されます(○3にも出力される気もするんですが。ついでに○1から入った電波は○2に、○2から入った電波は○1に出力されそうな気もします)。この時、○1から入った電波と○2から入った電波は○4の筒に入ったときに位相が逆になります。したがってその大きさは差になります。位相がなんで逆になるんかという理由を右の図に示します。でも、例えば○1から入った電波は○2にも出力される気がするので純粋に差じゃないんじゃないかなーとか思ったりします。
次に□Bです。今から測定を行おうというのですから、検出器を繋ぎます。終端抵抗を繋いじゃったらどこで測定するか分かりません。ちなみにここで検出器を選んだ時点で□Aは「差」だなと分かるので□Aは分からなくてもOKです。
次に□Cです。出力が□Cになった時に「標準可変インピーダンス」と「被測定インピーダンス」が同じになると書いてあります。問題を読むと「○1及び○2に任意のインピーダンスを接続して○3からマイクロ波を入力すると、等分されて○1及び○2へ進むが、反射波があると○4へ出力される。その大きさは、○1及び○2からの反射波の差である。」と書いてあります(□Aは□Bの問題を解いた時点で「差」とわかっています。)。○1のインピーダンスと○2のインピーダンスが等しければ、そこで生じる反射波の大きさは等しいはずです。そして、反射波が○4に入った時の電波の大きさは、○1から来た反射波と○2から来た反射波の「差」になるので、○4に入ったらその合成波の大きさは0になると考えられます。したがって□Cの答えは「最小」です。説明が長すぎました。今の説明がずばっとわかるかもしれない図を下に示します。
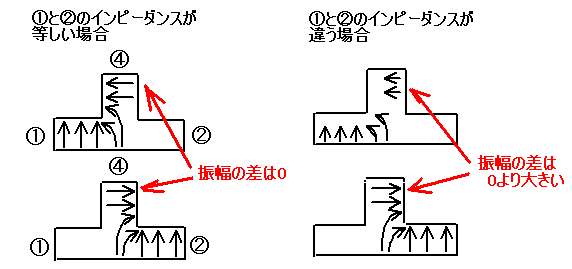
以上より、答えは1です。
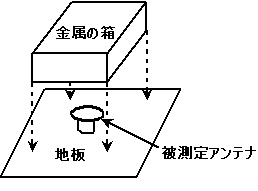 A-19 次の記述は、小型アンテナの放射効率を測定する方法について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。
A-19 次の記述は、小型アンテナの放射効率を測定する方法について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。
(1) 図に示すように、地板の上に置いた被測定アンテナに、アンテナの電流分布を乱さないようにした適当な形及び大きさの金属の箱をかぶせて隙間がないように密閉し、被測定アンテナの入力インピーダンスの□Aを測定する。この値は、アンテナからの放射がないので、損失抵抗Rl[Ω]とみなせる。
(2) 次に、金属の箱を取り除いて、同様にアンテナの入力インピーダンスの□Aを測定する。この値は、損失抵抗Rlと□B Rr[Ω]との和である。
(3) 放射効率ηは次式で得られる。
η=□C
| A | B | C | |
|---|---|---|---|
| 1 | 虚数部 | 導体抵抗 | Rl/(Rr+Rl) |
| 2 | 実数部 | 放射抵抗 | Rl/(Rr+Rl) |
| 3 | 虚数部 | 放射抵抗 | Rr/(Rr+Rl) |
| 4 | 実数部 | 放射抵抗 | Rr/(Rr+Rl) |
| 5 | 虚数部 | 導体抵抗 | Rr/(Rr+Rl) |
新問のような気がしますが、考えればなんとかなるでしょう。
まず□Aです。無線工学Bの試験において虚数が問題になるのはアンテナの短縮率と線路のインピーダンスくらいです。したがって□Aは実数部です。だといい加減ですね。問題を読むと「入力インピーダンスの□Aは、損失抵抗Rl[Ω]とみなせる」と書いてあります。抵抗Rは実数しかとりません。虚数が現れるのはコイルとコンデンサです。入力インピーダンス□Aは抵抗Rとみなせると書いてあるので、□Aは「実数」です。
次に□Bです。今はアンテナの話をしています。導体は関係ありません。アンテナに関係ありそうなのは「放射抵抗」な気がします。したがって□Bは放射抵抗です。
次にCです。科学の分野で効率といったら「入力したものに対して出力がどれだけあるかの比率」です。アンテナに電力を入力します。すると、その電力は放射抵抗と損失抵抗で消費されます。でも、本当は放射抵抗で消費されて欲しいのです(放射抵抗で消費された分だけ電波が飛んでいきます)。でも損失抵抗でも電力が消費されてしまいます。では、放射抵抗にどれだけ電力が行ったかな?という比率が放射効率です。したがって、放射効率は「放射抵抗/(放射抵抗+損失抵抗)」になります。
例えば、放射抵抗が9で損失抵抗が1だったら、放射効率は90%になります。これは入力電力の90%が電波として飛びましたという意味です。
ちなみに放射効率は問題によく出る気がするので覚えておいて損はないでしょう。
A-20 次の記述は、マイクロ波通信回線を設定する場合に行われる送受信点間の見通し試験の方法について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。
(1) 日中、鏡によって太陽光を反射されて相手側方向へ送り、相手側でこの光を観測して到来方向や上下の角度を測定する方法を□Aテストという。
(2) 相手側方向に光線をさえぎる高い森林や丘陵などがあり、□Aテストが困難な場合に□Bを上げ、これを望遠鏡などで観測してその方向を測定する方法をバルーンテストという。
(3) 夜間、電灯などの高原を利用し、その光を相手側で観測してその方向を測定する方法を□Cテストという。
| A | B | C | ||
|---|---|---|---|---|
| 1 | 太陽光 | 風船 | 照明 | |
| 2 | 太陽光 | 凧 | 夜間 | |
| 3 | 太陽光 | 風船 | 夜間 | |
| 4 | ミラー | 凧 | 夜間 | |
| 5 | ミラー | 風船 | 照明 |
試験馴れしていると、経験からくる勘で簡単に分かるのですが、試験馴れしていないとちょっと微妙かもしれません。
まず□B。バルーンと言ったら風船です。2陸技の問題って感じです。
□Aと□Cですが、こういう測定方法の命名はだいたい使う道具の名前がつきます。□Aは鏡を使うのでミラー、□Cは照明を使うので照明です。
したがって答えは5です。
B-1 次の記述は電界強度の計算式の誘導について述べたものである。□内に入れるべき字句を下の番号から選べ。
(1) 等方性アンテナの放射電力P0[W]、アンテナから半径d[m]における電界強度をE0[V/m]とすると、この点の□ア電力Wは、次式で表される。ただし、自由空間の固有インピーダンスを120π[Ω]とする。
W=E02/120π=□イ[W/m2]
上式から、E0=□ウ[V/m]となる。
(2) 任意のアンテナの絶対利得G(真値)は、等方性アンテナを基準アンテナとしたときの利得であり、等方性アンテナ及び任意のアンテナからそれぞれ電力P0[W]及びP[W]を放射したとき、遠方における両電波の電界強度が等しければ、G=□エ(真値)となる。
(3) したがって、絶対利得G(真値)のアンテナから電力P[W]を放射したとき、距離d[m]における電界強度Eは□オ[V/m]となる。
1 (30GP)1/2/d 2 ポインチング 3 2(30P0)1/2/d 4 P0/4πd2 5 P/P0
6 P0/πd2 7 ポテンシャル 8 P0/P 9 (30P0)1/2/d 10 2(30GP)1/2/d
陸技試験を受けるのならば、このレベルの問題がすらすら解けるほど数式を記憶しておく必要はあると思います。理解している必要はないですけど数式と言葉を記憶してください。
B問題は解答の選択肢のグループわけからはじめます。
セットになるのは、1と10、2と7、3と9、4と6、5と8です。
まず□ア。なんとか電力です。これは「ポインチング電力」です。ときどき出るのでこの言葉は覚えておいて損はないでしょう。
次に□イ。□イに入る数式の単位を見ると[W/m2]です。電力を距離の2乗で割っています。これを解答の選択肢から探すと、4と6のどちらかと分かります(Pの単位は[W]、πは無次元、dの単位は[m]ですね)。知らなければ後は運なのですが、答えは4です。この数式はよく出るので暗記してください。ちなみに、この「4πd2」は球の面積です。今回のような問題が出たら「あ、分母は球の面積だったなー」とか思い出すといいかなーと個人的に思います。これ以上の知識は参考書で「等方性アンテナ」を探すと出てくると思いますが・・・ちょっと数学が分からないとつらいかと・・・
□ウ。□イで6を選べば自動的に□ウは9になります。ちなみにこれは基本アンテナによる電界強度を丸暗記しておくと1ミリ秒で解けるでしょう。これを知っていれば逆算で□イが分かったりしてお得です。
□エ。□エに入る数式の単位は真値ということは無次元なので、5か8が入ります。ところで絶対利得Gというのはだいたい1より大きい値をとります。ということは、絶対利得Gを計算する式は分子の方が大きくて分母の方が小さくないと駄目です。ところで、実際に使うアンテナというのは等方性アンテナより利得が大きいです。したがって、実際のアンテナは小さい電力で大きな電界強度が得られます。ここで問題を読むと「遠方における両電波の電界強度が等しければ」とあります。遠方で電界をはかったら、等方性アンテナもあるアンテナも電界強度が10μV/mでしたとしましょう。その時、等方性アンテナには10W、あるアンテナには5W入力していたとしましょう。この時も利得はいくつでしょう?と聞かれたら、利得は1より大きい値をとるので、「等方性アンテナの出力/あるアンテナの出力」かな〜と思います。したがって答えは8です。
ちなみに、単純に「あ、実際に使うアンテナの方が出力が高いからPは分子だろ」と考えると間違えます。私は、昔これで間違えました。実際に使うアンテナは利得が高いから同じ電界強度を得るための出力は等方性アンテナに比べて小さくてOKです。
□オ。□ウがあっていれば1しか選びようがありません。でも、この数式はよく出るんで覚えてください。
ア:2 イ:4 ウ:9 エ:8 オ:1
B-2 次の記述は、図に示す3素子八木アンテナの動作について述べたものである。そのうち正しいものを1、誤っているものを2として解答せよ。ただし、波長をλ[m]としたとき、素子Qはλ/2、素子Rはλ/2より少し長く、また素子Dはλ/2より少し短いものとする。
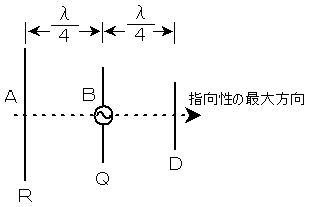 ア 素子QのB点から放射された電波が素子RのA点の到達したとき、その電波の位相は、素子QのB点より90度遅れる。この電波によって素子Rに電波と同位相の電圧が誘起される。
ア 素子QのB点から放射された電波が素子RのA点の到達したとき、その電波の位相は、素子QのB点より90度遅れる。この電波によって素子Rに電波と同位相の電圧が誘起される。
イ 素子Rが容量性リアクタンスであるため、素子Rに流れる電流の位相は、誘起電圧より90度遅れる。素子Rに電流が流れると、その電流より位相が90度送れた電波を再放射する。
ウ 再放射された電波が素子QのB点の戻ったとき、その電波の位相は素子RのA点より90度送れる。したがって、素子Qから出て素子Rによって反射されて素子Qに戻って来た電波の位相の合計は、180度となり、素子Qから放射された電波と逆位相になる。
エ 素子Qから放射された電波が素子Dに到達すると、その電波と同位相の誘起電圧を発生する。素子Dが誘導性リアクタンスであるため、誘起電圧より90度位相が進んだ電流が素子Dに流れ、この電流によって再放射される電波の位相は、電流より90度遅れる。
オ 素子Qから放射された電波が素子Dに到達してから再放射されるまでの位相の合計は零度となって、素子Dに到来する電波と同位相となる。
八木アンテナの問題はよく出てくるのですが、ここまで突っ込んだ問題は出てなかった気がします。
まずウ。素子Rで反射された電波がQに戻ってきた時、Qの電波と逆位相だったら、打ち消しあってしまうので反射器がある意味がありません。したがってウは×です。
次にオ。素子Qの電波と素子Dから放射される電波が同相だと強い電波になりますのでOKです。したがってオは○です。
ここまではあんまり考えずに分かります。
次にイとエですが、これは誘導性リアクタンスと容量性リアクタンスの意味を知っていれば即答できますが、知らないと答えられません。アンテナが半波長より長い場合は誘導性リアクタンス、短い場合は容量性リアクタンスになります。イではRは半波長より長いのに容量性と、エでは半波長より短いのに誘導性と言っていますので、イとエは×です。ここでウとイとエが×ですので自動的にアは○になります(この手の問題で×が4つとかは過去出たことが一回だけあったような気がきますが、3:2で選んでおいた方が無難です)。
参考 放射リアクタンス
ア:1 イ:2 ウ:2 エ:2 オ:1
B-3 次の記述は給電線について述べたものである。□内に入れるべき字句を下の番号から選べ。ただし□内の同じ記号は、同じ字句を示す。
(1) 平行2線式給電線は、平衡型の給電線であり、零電位は2本の導線の□アにある。特性インピーダンスは導体の太さが細いほど、また、導線の間隔が広いほど□イ。線路波長は、裸導線の場合、□ウの波長とほぼ同じである。
(2) 小電力用同軸ケーブルは、不平衡形の給電線であり、通常、零電位は□エ導体にある。特性インピーダンスは、内部導体の外径に対する外部導体の□オの比が大きいほど大きく、一般に線路波長は□ウの波長より短い。
1 二等分面上 2 内部 3 内径 4 外部 5 一方の導体
6 導波菅 7 大きい 8 自由空間 9 小さい 10 外径
まず選択肢のグループ分けです。2と4、3と10、7と9、1と5と6と8はよくわかんないので保留です。
まず同軸ケーブルと平衡ニ線式ケーブルのインピーダンスの式は覚えておいてください。
平行2線式給電線の特性インピーダンス
 のような平行2線式給電線の特性インピーダンスは、
のような平行2線式給電線の特性インピーダンスは、
Z0[Ω](特性インピーダンス) D[m](導線の間隔) d[m](導線の直径)
同軸線路の特性インピーダンス


Z0[Ω](特性インピーダンス) D[m](外部導体の内径) d[m](内部導体の外径) εr(比誘電率)
まず□アですが、平衡型の場合は一方の導体が行き、一方の導体が帰り、です。だから「平衡」なんです。したがって零電位は導体と導体の真ん中にあります。答えは1の「二等分面上」です。ちなみに同軸ケーブルのように不平衡型の場合は、外部導体が接地されてて電気が流れていないです。中心導体にのみ電気が流れます。だから不平衡です。したがって零電位は外部導体です。□エは4の「外部」です。同軸ケーブルは外部導体が接地されているので外部から入ってくる雑音が外部導体に遮断されて内部までこれません。だから、平衡型の線路より損失が少ないです。
□イは上の式より導体が細くて広いほどインピーダンスは大きくなりますので、「大きい」です。導体は細いほど電気が流れにくくなって抵抗が大きくなりますので直感的にもインピーダンスが大きくなることが分かるかなーと思います。
□オは上の図より「内径」です。覚えておいて損はないので覚えましょう。
□ウは(2)の問題の方を見ます。「同軸線路は一般に線路波長は□ウの波長より短い」です。ここに入りそうな選択肢で残っているのは「自由空間」「導波管」の2択です。どっちと比べるかといったら「自由空間」と比べるだろと素朴に思いますので答えは「自由空間」です。電波の世界では何事も「自由空間」が基準になります。
ちなみに、同軸ケーブルの中の電波の波長が自由空間より短くなるのは誘電体が含まれているからです。この事実も覚えておくとうれしいです。
ア:1 イ:7 ウ:8 エ:4 オ:3
B-4 次の記述は、発生源によって分類した電波雑音について述べたものである。□内に入れるべき字句を下の番号から選べ。
(1) 自然雑音には、空電雑音、太陽雑音及び□アなどがある。空電雑音には、主に、□イの周波数を使用する無線通信に、また太陽雑音は、宇宙通信などにおいて、受信アンテナの指向性の最大方向が□ウに向いたときに大きな影響を与える。
(2) 人工雑音には、自動車のイグニッション系機器、電気機器及び送電線から発生する雑音などがあり、□エで多く発生する。特に、イグニッション系機器から発生する雑音は□オ性の雑音であり、VHF帯からUHF帯での無線通信に著しい影響を与える。
1 宇宙雑音 2 月 3 VHF帯以上 4 都市部 5 トランジスタ雑音
6 HF帯以下 7 連続 8 太陽 9 衝撃 10 郊外
まずグループわけです。1と5、2と8、3と6、4と10、7と9です。
□アは自然雑音が入るので1の宇宙雑音です。トランジスタは人工ですよね。
□イは周波数帯域を選びます。(2)の人工雑音ではVHFとUHF帯の話をしています。このことから、(1)ではHF帯の話をしているのではないかと推測できるので、□イは6のHF帯以下です。
□ウは月か太陽が入ります。どう考えても雑音が大きそうなのは太陽です。
□エは都市部か郊外が入ります。どう考えても都市部の方が雑音が大きそうです。
□オは衝撃か連続が入ります。私歯イグニッションというのを知りませんが(イグニッションキー?)、問題文中に「特に、イグニッション系機器から発生する雑音」とあります。イグニッション系機器の雑音は特別らしいです。そして「送電線から発生する雑音」は連続と衝撃のどちらかと言えば電気は常時流れているので「連続」な気がします。したがって□オは9の衝撃です。
ア:1 イ:6 ウ:8 エ:4 オ:9
B-5 次の記述は、方向性結合器を用いて同軸給電回路の反射係数及び定在波比を測定する原理について述べたものである。□内に入れるべき字句を下の番号から選べ。
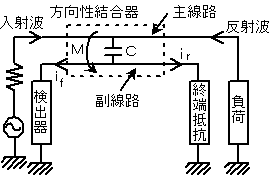 図に示すように、方向性結合器の主線路と副線路は、静電容量C[F]及び相互インダクタンスM[H]によって結合されており、主線路には特性インピーダンスZ0[Ω]の同軸給電線が、また、副線路には電流を測定する検出器と終端抵抗R[Ω]が接続されているものとする。ただし、検出器の内部抵抗と終端抵抗は等しく、副線路の自己インダクタンスL[H]、角周波数をω[rad/s]とすると、ω<<R及びR<<1/(ωC)のときのM=CRZ0の関係があるものとする。
図に示すように、方向性結合器の主線路と副線路は、静電容量C[F]及び相互インダクタンスM[H]によって結合されており、主線路には特性インピーダンスZ0[Ω]の同軸給電線が、また、副線路には電流を測定する検出器と終端抵抗R[Ω]が接続されているものとする。ただし、検出器の内部抵抗と終端抵抗は等しく、副線路の自己インダクタンスL[H]、角周波数をω[rad/s]とすると、ω<<R及びR<<1/(ωC)のときのM=CRZ0の関係があるものとする。
(1) 主線路上の電圧をV[V]、電流をI[A]とすると、静電結合により静電容量Cを通り検出器と終端抵抗に二分され、副線路に流れる電流icはVに比例し、次式で表される。
iC=□ア[A] ・・・○1
また、誘導結合により副線路に流れる電流iMは、Iに比例し、次式で表される。
iM=□イ[A] ・・・○2
(2) iCとiM合成電流は、誘導結合の方向によりそれらの和又は差となるが、ここでは検出器側の電流if[A]が和、終端抵抗側の電流ir[A]が差となるように回路が構成されているものとすると、ifは次式で表される。
if=iC+iM=□ウ[A] ・・・○3
(3) 入射波のみのときはV/I=Z0であり、条件からM=CRZ0であるから○3式は次式となる。
if=□エ[A]
また、負荷側からの反射波のものときにはiの符号が変わるから、if=0となる。この場合、方向性結合器に接続されている検出器と終端抵抗を入れ替えると、この反射波電圧に比例した電流を測定できる。このようにして、入射波電圧と反射波電圧を測定し、それらの□オから反射係数を求め、定在波比を算出する。
1 jωMI/2R 2 jωCV/2R 3 jω(CV/2R+MI/2R) 4 jωCV/2 5 jωMI
6 jωMI/2 7 比 8 積 9 jω(CV/2+MI/2R) 10 jωCV
問題文をよく読まなくても次元を調べるだけでさくっと解答が導き出せるとってもお手軽問題です。
まずグループ分けから。1と6、2と4、3と9、5と10、7と8です。ここで「1と2、4と6っていうグループ分けの仕方もあるんじゃないか?」と思うかもしれません。でも、それは間違いです。陸技の試験で数式を選ばせる問題は分子に2が入っていたり余計な文字が入っていたりルートになっていたり、分母に2が入っていたり余計なものが入ってたりルートになっていたりして、それのどっちかを選ばせるのが大半だからです。だから1と6、2と4にグループ分けします。そうすると、5と10が余っちゃうので、これはこれでグループなんだなと思います。
□ア。□アの左辺はiCとなっています。このことから「あ、Cが関係あるんだな」と分かります。とすると、選択肢の中でCが出てくるのは、2と4と10です。グループ分けでは2と4、1と10としました。このことから「あ、2か4を選ばせる問題なんだな」と解釈します。2と4の違いはRがあるかないかです。さて、□アの次元は[A]=[V/Ω]です。したがって答えは4です。2の次元は[V/R2=I/R]ですよね((1/jωC)[Ω]、R[Ω]、V[V]です。)。
□イ。□イの左辺はiMとなっています。このことから「あ、Mが関係あるんだな」と分かります。とすると、1か6を選ぶんだなと分かります。さて、□イの次元は[A]です。したがって答えは1です(jωM[Ω]、R[Ω]、I[A]です。)。
□ウ。足し算していることから、3か9のどちらかであると速攻で分かります。□アと□イが出来ていれば、答えは9とすぐに分かります。さて、この3と9を見ると「jω(MI/2R)」が共通にあることが分かります。このことから□イの答えは1しかありえないことが分かります。
□エ。□ウが分かればV/I=ZとM=CRZ0を代入して答えは10と分かります。
□オ。係数と言ったら「比」しかありません。したがって答えは7です。
一応□アから解いていきましたが、あんまり考えずに解くのでしたら、まず□ウから見ます。ここで□ウを見るととりあえず□イの答えが1と分かります。次に□ウの候補は3か9ですけど、これにV/I=ZとM=CRZ0を入れて計算してみます。すると、9の方はすんなり選択肢の10の形になるんですが、3の方はいくらいじっても駄目そうだと分かります。したがって□ウは9、□エは10と分かります。□ウが9と分かれば自動的に□アは4しかありえません。
こんな感じで二陸技の試験で式が出てくる場合は、選択肢じっくり見てと次元を調べるだけで問題をよく読まなくても解けるというお手軽さがあります。
ア:4 イ:1 ウ:9 エ:10 オ:7