二陸技

平成12年1月

　この問題は知らないと解けません。

ポインチング電力（覚えているとうれしい）

　Ｗ[W/m²]（ポインチング電力）　Ｅ [V／m]（電界）
　私は未だにボインチング電力ってのが何者か知りませんが、まあこの式だけはなんとなく覚えておいてください。

　まず無線の試験でベクトルと言ったら、ポイチングベクトルしかないです。よって□Cはポインチングです。
　また、強度と言ったら電界強度しかないです。したがって電磁界強度というのはないので□Aは電力密度です。
　ちなみに、上の式の120πという数字がどこから出てくるかを考えると大学の電気科程度の勉強が必要になるので深く考えずに、E²/120πを暗記するのがよいでしょう。
　答えは5です。解説になってませんね・・・

A-2　次の記述は、フリスの伝送公式について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。
(1)　図に示すように、入力電力がP_t[W]の無指向性で損失が無い送信アンテナから半径d[m]の球面上における電磁界の電力密度は、P_t/(4πd²)である。したがって、絶対利得がG_tの送信アンテナに同じ電力を供給したとき、送信アンテナから半径d[m]の球面上でアンテナの最大指向方向の点における電力密度は次式となる。
　p=□A　[W/m²]
(2)　この送信アンテナの実効面積をA_t[m²]とすれば、上式は次式となる。
　p=□B　[W/m²]
(3)　この電波を実効面積A_r[m²]のアンテナで受信したとき、アンテナから取り出すことのできる最大電力P^rは、次式となる。
　P_r=□C×P_t　[W]

　何も知らなくても2択にまでは持ち込めます。
　□Bの答えの単位は[W/m²]、そしてこの電波を実効面積A_r[m²]のアンテナで受信したとき□Cとなると書いてあり、□Cの答えの単位は[W]です。故に□Bに[m²]をかけると□Cの答えになります。[m²]は面積です。この問題に出てくる面積と言ったら実効面積しかないです。したがって□Bに実効面積((3)の問題文に出てくる実効面積はA_rです)をかけたものが□Cの答えとなります。
　□Bと□Cを見ると、□BにA_rのみがかけてある選択肢は、1と4しかありません。あとは運です。
　しかし、利得Gの扱い方だけは知っておいた方がいいです。利得Gは、真数計算の時は電力にかけ算しますです。対数計算(dBに換算しているとき)は電力に足し算します。今回は真数計算なので電力にかけます。したがって、□AはP_t/(4πd²)にかければいいので、答えはP_tG_t/(4πd²)です。
　以上のようにも解けるのですが、この手の問題はよく出ますので原理?を覚えるとうれしいです。まず下の公式は覚えてください。

マイクロアンテナの受信点の電力密度（重要）

　W₀[W/m²](電力密度)　P_t[W](送信電力)　G_t[単位なし](送信アンテナの絶対利得)　d[m](送信アンテナからの距離)

アンテナの実効面積などなど（重要）

　Ａ_e[m²]（アンテナの実効面積）　Ａ [m²]（アンテナの面積）　λ [m]（波長）　Ｇ [単位なし]（利得）　η[単位なし]（開口効率）

フリスの伝達公式の使い方(重要)

　まず上の図のような構成を考えます。アンテナ(利得なし)から送信電力P_tで電波を出すと距離dの位置での電力密度W[W/m²]はP_t/4πd ²です。

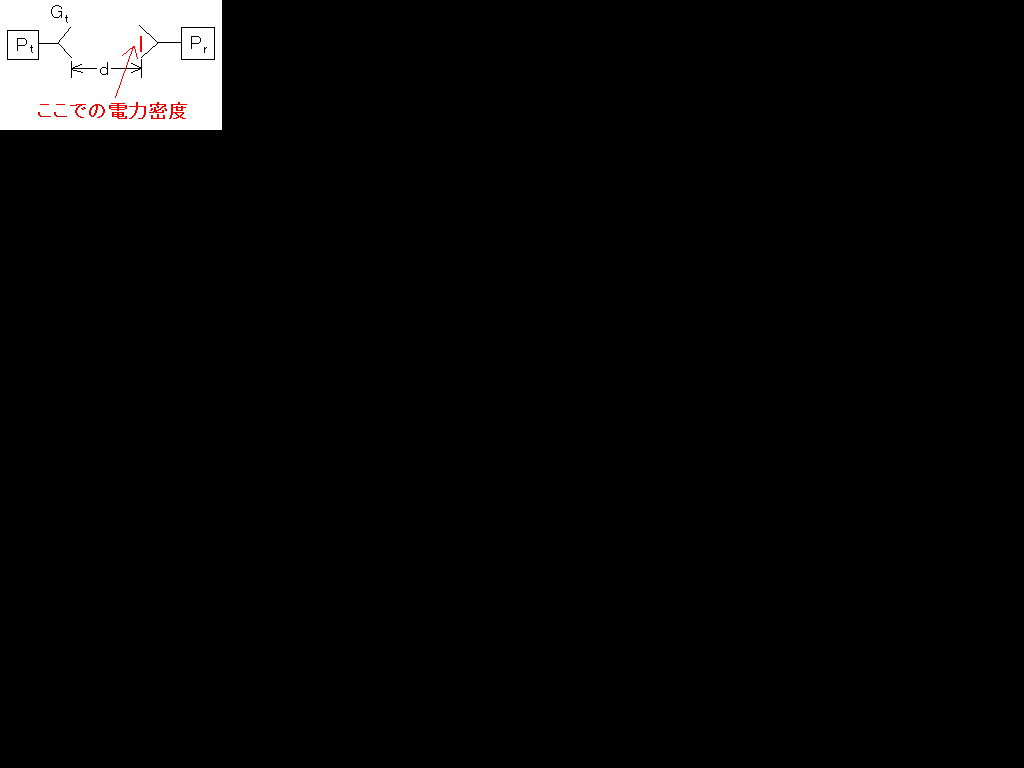
　次に、アンテナに利得がG_tあったとします。すると距離dの位置での電力密度W[W/m²]はP_tG_t/4πd ²です。

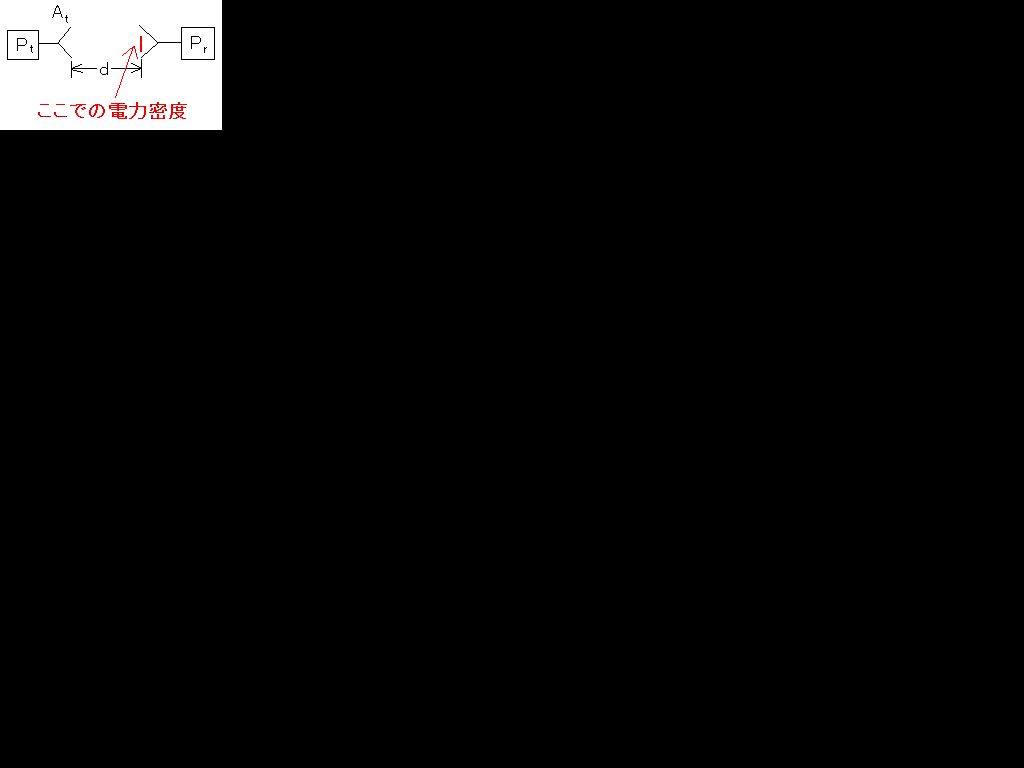
　利得がG_tではなくて、実効面積A_tが与えられた場合は、まずA_e=λ²G/4πを思い出します。これをG=の式になおすと、G=4πA_e/λ²。これをP_tG_t/4πd ²のG_tに代入すると、電力密度W[W/m²]はA_tP_t/λ²d ²です。

　今度は送信アンテナの利得がG_t、受信アンテナの実効面積がA_rだったとします。P_r(受信電力)[W]=W(電力密度)[W/m²]×A_r(実効面積)[m²]です。W[W/m²]はP_tG_t/4πd ²なので、P_r(受信電力)[W]=P_tG_tA_r/4πd ²です。

　それでは、送信アンテナの利得がG_t、受信アンテナの利得がG_rだったとすると、P_r(受信電力)[W]=P_tG_tA_r/4πd ²のA_rにλ²G/4πを代入するだけです。結果、P_r(受信電力)[W]=λ²P_tG_tG_r/(4πd)²となります。この式はよく見ます。

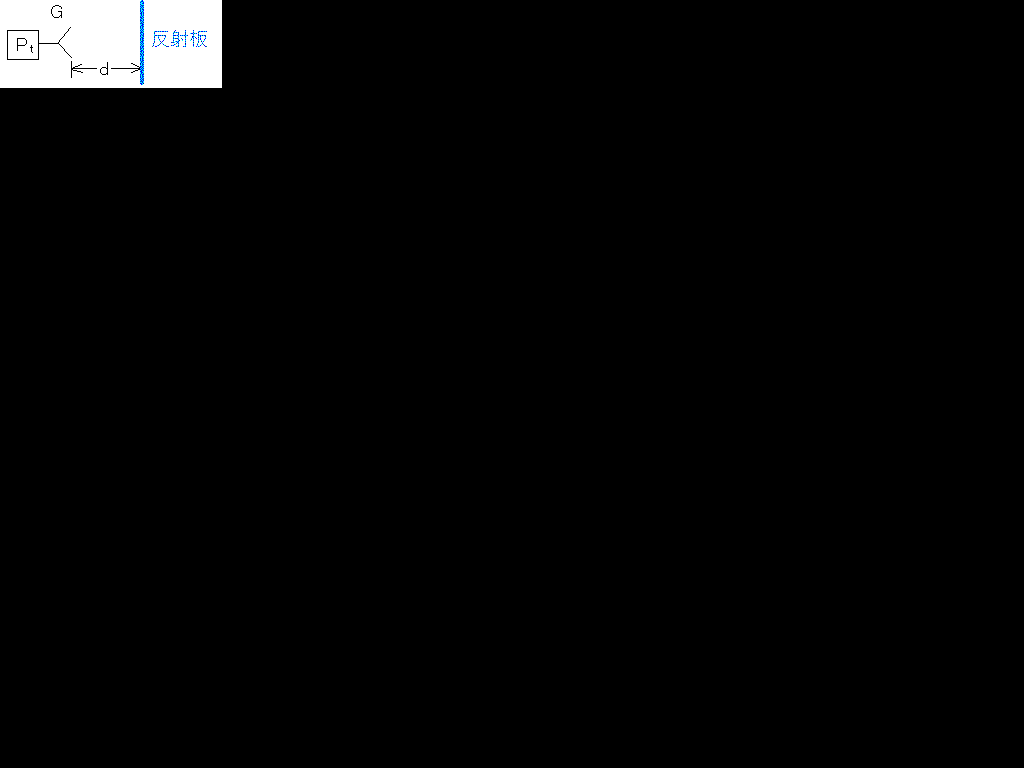
　ときどき、上の図のように受信アンテナと送信アンテナを共用して利得を計算したりする問題が出ます。この場合は、送信利得、受信利得が共にG、距離を2dとして上の式にいれればいいので、P_r(受信電力)[W]=λ²P_tG²/(4π(2d))²=λ²P_tG²/(8πd)²となります。利得が知りたかったら、この式をG=になおせばよいです。
　この程度のことは出来るようにしておくとよいでしょう。

　知らないと分からない問題です。
　絶対利得とは等方性アンテナを基準とした任意のアンテナの利得です。
　相対利得とは半波長ダイポールアンテナを基準とした任意のアンテナの利得です。
　半波長ダイポールアンテナの絶対利得は1.64(2.15[dB])です。当たり前ですけど、半波長ダイポールアンテナの相対利得は0[dB]です。
　指向性利得とはあるアンテナから電波が全方向へ均等に放射されたとしたときの放射強度に対する特定方向への放射強度の比です。
　指向性利得×アンテナ効率(<1)=絶対利得

　完全半波長アンテナと半波長ダイポールアンテナは同じだと思います。
　まず、1ですが表から分かる通り等方性アンテナの相対利得は-2.15[dB]です。したがって答えは1です。次に2の完全半波長アンテナの絶対利得は表の通り2.15[dB]です。3は、指向性利得×アンテナ効率=絶対利得なので損失がないということは効率が100%なので、指向性利得×100%=絶対利得なので、指向性利得=絶対利得です。4は表の通りです。等方性アンテナの絶対利得は0[dB]、アンテナ効率は100%であるので指向性利得は0[dB]です。

A-4　図に示す長さが半波長程度のダイポールアンテナの給電素子abからみたインピーダンスZ_abが次式で与えられるとき、Z_abを純抵抗とするためのアンテナ素子の短縮率の値として、最も近いものを下の番号から選べ。ただし、素子を短縮する割合をδとし、ダイポールアンテナの特性インピーダンスZ₀は純抵抗で420[Ω]とする。
　Z_ab≒73.1+j42.6-jZ₀πδ
1　1.6[%]　2　2.3[%]　3　3.2[%]　4　4.8[%]　5　5.5[%]

　式が与えられている場合、式に問題で与えられた値を入れれば解けます。またこの問題は短縮率と言う言葉を知らなくても、純抵抗と意味を知っていれば解けます。
　Z_abが純抵抗になるということは、リアクタンス成分（jがついている項）がないということです。ということで、j42.6-jZ₀πδが0になれば良いということです。Z₀は問題文に420と与えられているので、j42.6-j420πδ=0として、δを求めればよいです。答えは0.032で3.2%です。

短縮率
　半波長ダイポールアンテナはZ≒73.1+j42.6のように放射抵抗以外に放射リアクタンスを持ちます。このリアクタンス成分があると、給電する場合に整合回路が複雑になります（純抵抗だけだったら抵抗だけ考えて整合とればいいですけど、リアクタンスが入っていると抵抗とリアクタンスの両方を考えて整合を取らないとダメなのでめんどくさそうです）。
　アンテナを少し短くすると放射リアクタンスが零になる点が存在します。この短くする割合を短縮率といいます。
　なんで短くすると放射リアクタンスが零になるかは、難しい本を読んでください。

　イメージはこんな感じです。

　選択肢に400[Ω]、1.25[kΩ]、2.5[kΩ]なんてありますが、どう見てもそんな値になるとは思えません。常識で選んでいいのは35[Ω]か100[Ω]です。
　式が与えられているのでそれに代入するだけで解けますが、ちょっと式を操作しないと解けないのが一陸技な気がします。

位相定数β
　β=2π/λ

　これを使ってtanβlを計算すると、tan(π/2)=∞となってしまいます。そこで式を変形する必要があります。

　このZ₀に50[Ω]、Z_rに25[Ω]をいれて、Zは100[Ω]です。
　ところで、

1/4波長整合回路
のとき、
　Z₀[Ω]（特性インピーダンス）　Z_q[Ω]（1/4波長整合回路の特性インピーダンス）　R[Ω]（負荷抵抗）

を見ると、この問題のZ₀がZ_q、ZがZ₀にあたります。陸技の試験で入力側から見たインピーダンスを求めろと言った場合この1/4λ整合回路しか出ないです。よって、この問題の難しい式は覚えないで上の1/4波長整合回路の式を覚えて、それにいろんな値をいれて計算してみれば答えは出ると思います。1/4λじゃない場合が出てきたら、しょうがないので上の難しい式を解きます。でも出ないでしょう。
　でも、位相定数β=2π/λは覚えて置いた方が良いです。何かで使った気がします。

　出題者が苦労して問題考えたんだろうなあということが伺える問題です。
　まず□Aですが、芯線のない同軸ケーブルなんてあるはずないので「遮断波長」です。分からない方はテレビにささっている同軸ケーブルでも見てみてください。
　□Bですが、無線の試験に出てくるのは誘電体だけです。磁性体は出てきません。ちなみに磁性体というのは磁石です。同軸ケーブルに磁石入っていたら恐ろしいです。
　□Cですが、大きいのと小さいの、どちらが実用的じゃないかと言ったら常識的に考えて大きい方です。配線するときには線は小さい方がいいに決まってます。したがって答えは大きいです。
　結局答えは、1です。

　ちなみに遮断波長は導波管による伝搬可能の最大波長のことを言います。陸特ではこの遮断波長を求める計算が出るのですが陸技では出ないので公式は覚えなくてもいいと思います(2000年6月現在)。

　知らないと解けませんが、私ならば問題文中の赤い部分に注目します。どちらも狭帯域の特性であると書いてありますが、こういう場合はどちらかが誤りです。よって私ならば3か4を選びます。
　陸技を受けるつもりならば絶対に選んではいけないのは、1です。整合回路はインピーダンスが異なると定在波が生じてしまうため挿入します。
　バランとスタブはどちらも整合回路の一種です。バランは同軸線路（不平衡線路）と平行2線式線路（平衡線路）の接続に使われます。
　変成器は広帯域な特性をもつそうです。答えは4だそうです。

バラン

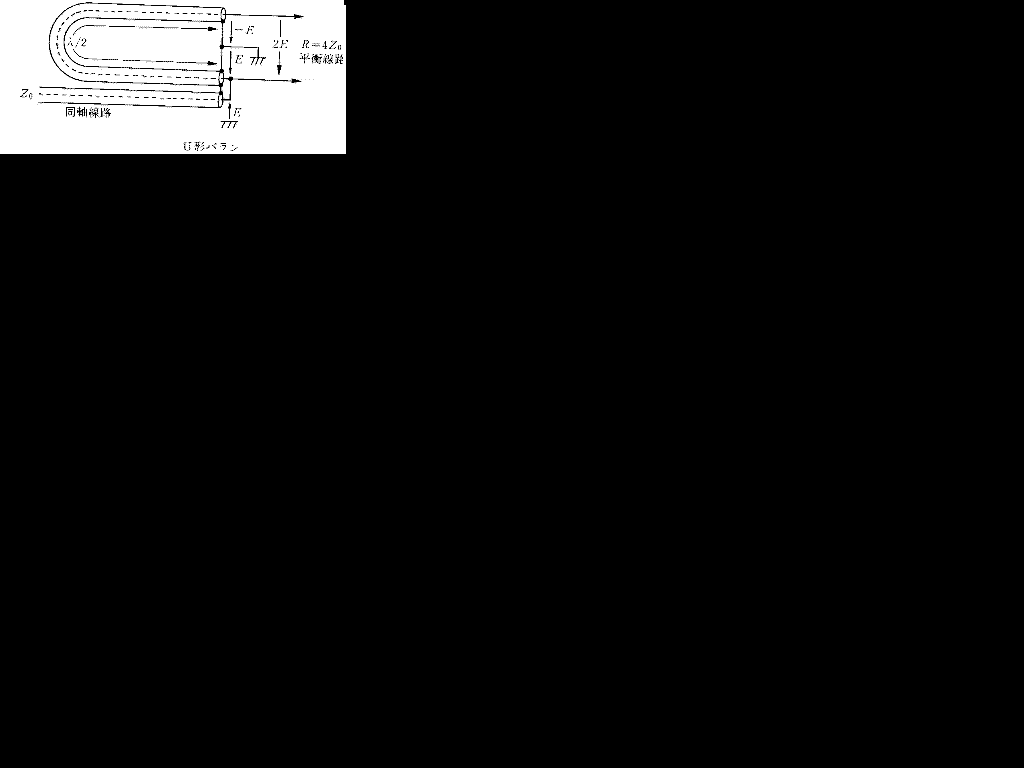
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B　東京電気大学出版局　1992　の21ページより抜粋しています。

スタブ

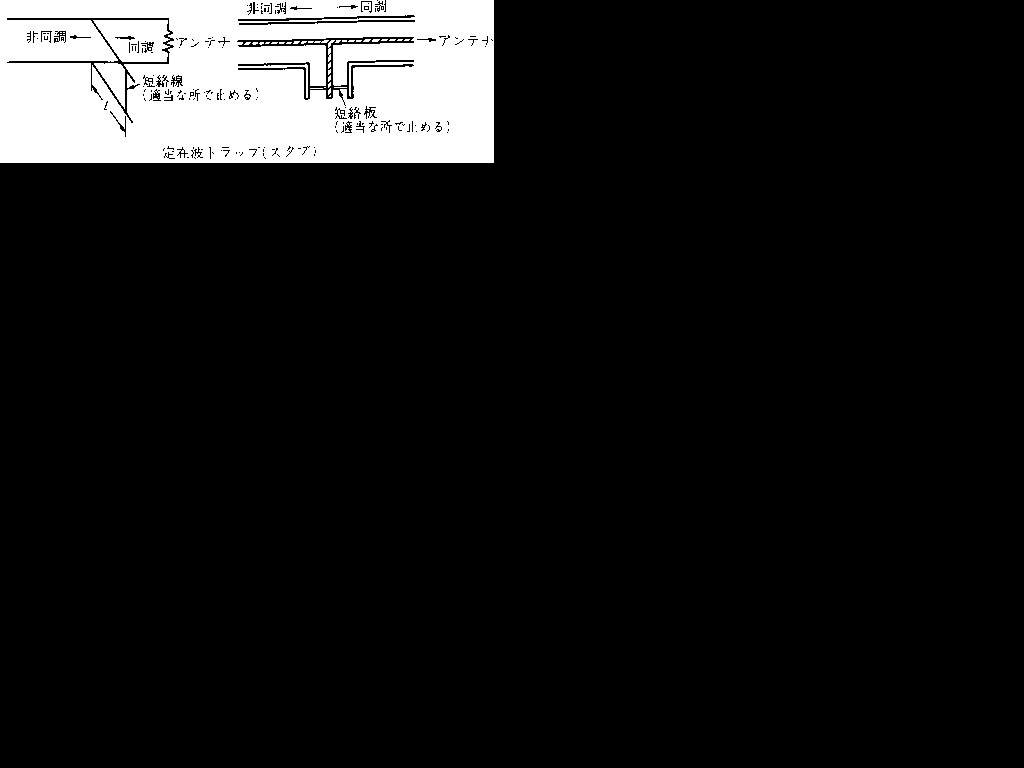
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B　東京電気大学出版局　1992　の19ページより抜粋しています。

　知らなきゃ分かりません。
　なんとか比と言った場合普通は「0〜1」の値をとるもの、「1〜∞」の値をとるものの２種類があります。この問題の場合、1の選択肢だけが0.64と1より小さいです。他の値は1を越えた値です。「1〜∞」までの候補が4つあります。したがって、定在波比は「1〜∞」までの値をとるんだろうと予測できます。したがって、1は選べません。

電圧定在波比と反射係数の定義(まあ重要)

　S[単位なし](電圧定在波比)　Γ[単位なし](反射係数)

電圧定在波比と反射係数の相互変換(重要)

　S[単位なし](電圧定在波比)　Γ[単位なし](反射係数)

　上の式からまずΓを求めます。
　Γ=(75-50)/(75+50)=0.2
　次にSを求めます。
　S=(1+0.2)/(1-0.2)=1.5
　答えは1.5です。

　まず、□Bは分かります。「外部雑音が混入する恐れ」がありそうなのは、開放です。したがって選んでいいのは1か3か5です。あとは運です。
　下にマイクロストリップ線路の構造を示します。

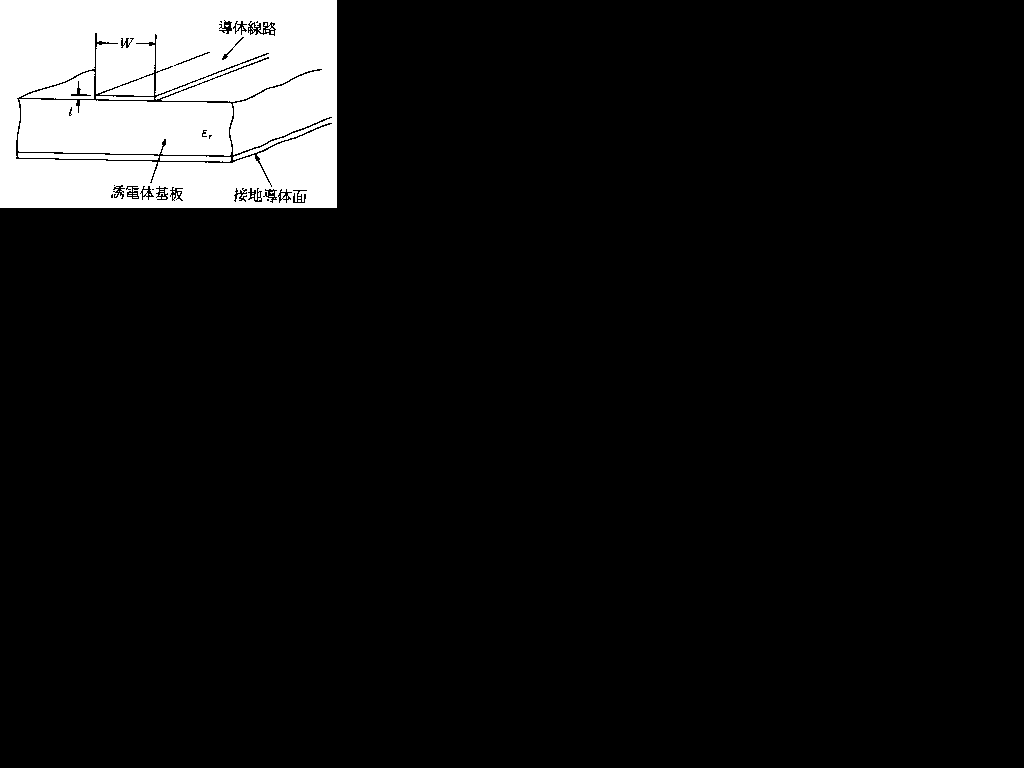
　誘電体基板の上にあるのは導体線路なので、□Aは導体です。そんなこと知らなくても「接地した導体」と「誘電体」だけじゃ電気が流れない（流れるけど、滅茶苦茶流れにくいでしょう）ので、導体が上にのっかってないと駄目だなというのはちょっと考えれば分かるでしょう。
　□Cは知らないと分からないです。「大きく」です。放射損失が小さいというのは線路のインピーダンスが小さいということです。マイクロストリップ線路は同軸線路を平たくして天井をとってしまったものと考えられるそうです。下の図を見てください。対称ストリップまでしか載ってませんけど、天井をとればマイクロストリップです。

上の図は内藤喜之著『マイクロ波・ミリ波工学』コロナ社　1986の38ページより抜粋しています。
　要するにだいたい同軸線路と性質は似ているだろうということです。同軸線路のインピーダンスは

です。ε_rが大きい方がZ₀は小さくなるので、答えは「大きく」です。要するにεは分母にくるということを覚えておけばいいということだと思います。あとは難しい本読んでください。私は分かりませんでした。

　まず、無線の試験においては長さとか波長とか言われたら1/4波長です。よって□Aは1/4波長です。
　□Bはその後の文章に「漏れ電流が阻止される」と書いてあります。インピーダンスが大きい方が電流が流れにくく漏れ電流が阻止されそうです。したがって、□Bは「高く」です。
　垂直半波長ダイポールアンテナの指向性は無指向性です。自明でしょう。どんな指向性か？と聞かれたら水平面の指向性の場合は無指向性と答えるのが無難です。単一指向性とか双方向性とかは今まで出たことがない気がします。
　一応下にスリーブアンテナの図を載せます。見れば分かりますけど、水平面内の指向性はどうみても無指向性にしかなりそうにないですよね。

　知らなきゃわかりませんが、滅茶苦茶よく出るので陸技を受けるならば公式を覚えて使えるようにしておくべきでしょう。

アンテナの実効面積などなど（重要）

　Ａ_e[m²]（アンテナの実効面積）　Ａ [m²]（アンテナの面積）　λ [m]（波長）　Ｇ [単位なし]（利得）　η[単位なし]（開口効率）

　波長λ[m]=3.0×10⁸/周波数=3.0×10⁸/10×10⁹[Hz]=0.03
　利得G=50[dB]=10⁵
　実効面積A_e[m²]=λ²G/4π=(0.03)²×10⁵/4π=7.166
　アンテナの面積A[m²]=2×2×3.14=12.56
　開口効率η=A_e/A=7.166/12.56=0.57
　よって答えは2です。

　私はなんとなく3かと思っていたのですが、答えは4だそうです。
　まず2は選んではいけないです。面積が大きければアンテナが大きくなるので実効高も大きくなりそうです。巻き数の方は実効高の式を見てください。

ループアンテナの実効高

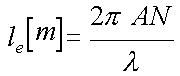
　l_e[m]（アンテナの実効長）　λ[m]（波長） A[m²]（ループ面積）　N[回]（巻き数）

　1,4,5についてはまず下の図を見てください。

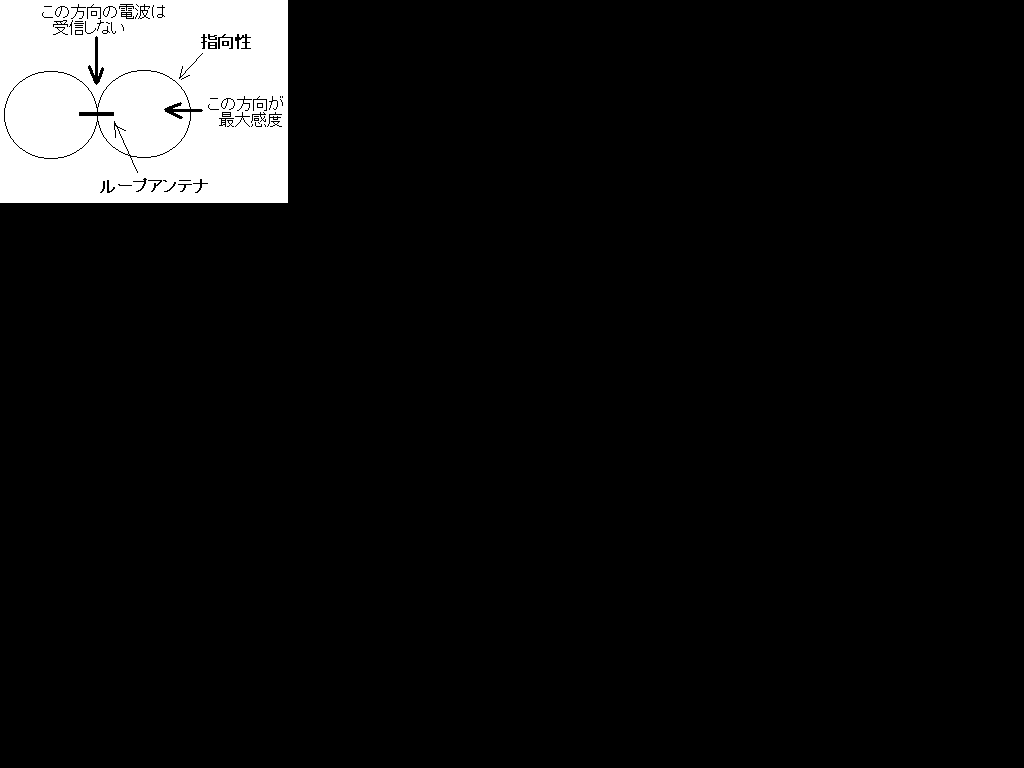
　これは水平面の指向性です。というわけで、1はあっています。4は見ての通りループ面に直角な方向には指向性の線がないので電波を受信しないです。感度が最大になるのはループ面と水平?な時です。5ですが、電波の到来方向がループ面に対して直角だと受信電界強度が0になりますが、その性質が方向探知に利用されます。ループアンテナを動かして受信電界強度が0になったらその右90°か左90°から電波がきているってのが分かります（これは私が書いているときに考えながら書いたので嘘かもしんないです、でも方向探知に使われるのは事実です。）。3ですが、そういうものらしいです。とりあえず覚えておきましょう。

　レードームがなんだか知らなくても考えれば解けるでしょう。
　まず、□Bですが(1)の問題に「通過する時」と書いてあります。したがって透過率が良い方がいいに決まっています。したがって□2は透過率です。
　次に、□Cですが(1)の問題に「誘電体で作られている」と書いてあります。したがって生じる損失は誘電体損に決まってます。したがって、□3は誘電体損です。
　さいごに□Aですが、駆動機構みたいです。

　知らなきゃ出来ませんが、自由空間伝搬損失（自由空間基本伝送損失とも言うんですね）の式は覚えておくべきでしょう。
　少なくとも3は選んではいけません。なぜなら、1と4は「3.1」で、2と5は「9.9」になっているからです。仲間はずれは3の「2.5」です。

自由空間伝搬損失Γ

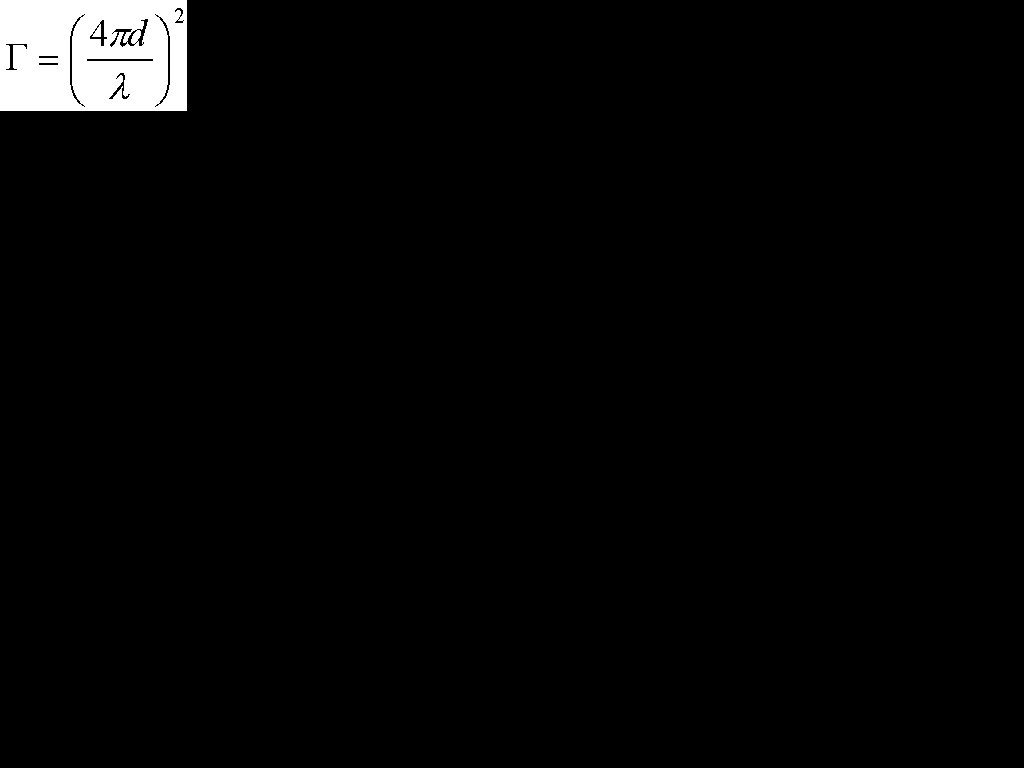
　Γ［単位なし］（自由空間伝搬損失）　d［m]（距離）　λ[m]（波長）
　ΓはdBになおして使用することが多いです。その時は、10log₁₀Γです。
　この式を見て分かることは、伝搬損失は距離の2乗に比例して増えて（要するに距離が増えると損失は増える、当たり前だけど）、波長の2乗に反比例して損失は増える（要するに波長が長ければ長いほど損失が小さい）。

　上の式のdに50×10³、λに2を入れて計算するだけです。ちゃんと計算しなくても、50×10³を2乗すると10⁸を越えるので答えは5かなあと分かります。

　知らなきゃわからないですが、知らなくて当然です。この問題は解けなくていいと思います。送信電力の値を求める公式で覚えるべきものは、半波長ダイポールの場合、等方性アンテナの場合、よくて微小ダイポールアンテナの場合です。しかも送信電力を求める問題は陸特にはよく出るのですが、陸技には出ないです。したがって、あんまり覚えていなくてもいいと思います。一応解答を。

λ/4接地アンテナによる電界強度

　E[V/m](受信電界強度)　P[W](送信電力)　d[m](送信アンテナからの距離)

　上の式に各値を代入して、答えは918[W]になり、値が近いのは4です。

　まず、「二つ以上の通路を通る」とあったら干渉性フェージングです。したがって、Aは干渉性です。
　電離層を通過すると、だ円偏波になります。直線偏波は垂直偏波の波と水平偏波を合成したもですが、これが電離層で反射すると垂直偏波になるとは考えられません。
　□Cは問題文中に「偏波面が変動する」とあるので、偏波性を選びます。
　したがって答えは2です。

　ちなみに跳躍性フェージングというのは、電離層状態が変化することによって電波の反射の具合がかわり電界強度が変動すること、と自分は思っています。
　偏波って何？という方は、適当な本を買ってください。ちなみに円偏波が空間が伝わっていく様子がTOSHIBA CORPORATIONの円偏波伝搬模式図にありますのでぜひご覧下さい。

　日本語を知っていればいけそうな気がする問題です。
　□Aは「□A及び湿度」となっています。湿度と対になっているのは、気温です。したがって、□Aは気温です。
　電波が何で屈折するかというと、空気があるからです。空気は上にあがるにつれて薄くなります。したがって、空気が薄くなれば屈折率は減少すると考えられます。したがって、Bは減少です。
　等圧線図というのは、いつも天気予報でみている天気図のことです。あの図を見ても屈折率なんてわかりません。したがって、CはM曲線です。
　答えは2です。

　まず分かるのが□Bです。「推定によって求める」というのは明らかにおかしいです。「計算によってもとめる」ならわかります。よって□Bは計算です。
　知っていれば分かるのが□Aです。

微小ダイポールアンテナの距離rにおける電界（覚えているとうれしい）
　Ｅ [V／m]（電界）　r [m]（距離）
　この式自体は覚えないで、放射電磁界は距離rに反比例して誘導電磁界ってのは距離rの2乗に反比例するんだなってことと、距離rが大きいと誘導電磁界と静電界は距離の2乗とか3乗に比例するので無視していいことを覚えておけばおっけーです。

　遠方ですとrが十分に大きいときは1/rの放射電磁界しかのこらないです。したがって、□Aは放射です。
　電波星はそういうものがあって、測定に使えるということを頭の隅においておけばいいと思います。

A-19　次の記述は、図に示す回路構成により接地アンテナの実効抵抗を測定する方法について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。

(1)　高周波発信機Oを測定□Aで動作させ、スイッチSを○1側に倒してアンテナ同調用コンデンサC₀で同調をとり、そのときの高周波電流計○Aの指示値Iを読む。
(2)　アンテナ同調用コンデンサC₀をそのままにしてスイッチSを○2側へ倒し、可変コンデンサC_Sと可変インダクタンスL_Sを調整して高周波電流計○Aの指示値を□Bにし、標準可変抵抗R_sを加減して高周波電流計○Aの指示値がIと等しくなるように調整する。このときの□Cの値がアンテナの実効抵抗である。

　□Aですが、無線の試験では「強度」という言葉は出てこないです。出てくるとしたら電界強度です。したがって□Aは周波数です。
　□Cは、「□Cの値がアンテナの実効抵抗である」とあるので、抵抗が知りたいわけです。したがって、標準可変抵抗の値を読みます。コンデンサとかインダクタンスを読んでもしょうがないです。
　□Bは、知らないとできないですが、おぼえておきましょう。回路が共振したとき、リアクタンスがなくなって電流が最大になります。電流が最大になったときリアクタンスがなくなって抵抗成分だけになるのでCは最大です・・・分かりますか？　共振したとき、電流が最大でリアクタンスは0になると覚えてください。 　したがって答えは3です。

　こういう問題を見たら、まず次元を調べます。P=EI=E²/Rですので、分母はE²、分子はRになっていないと駄目です。したがって、選択肢の5は絶対に選んではいけません。
　あとの式の展開は過去問をみてください。面倒です。答えは1だそうです。この問題は式の過程を記憶、理解するより式を丸暗記の方がいいと思います。

　この問題は陸技の問題としては超基本的で、これくらいはすらすら出来るようにしてください。
　それはいいとして、B問題は正しいものを1、間違っているものを2とする問題以外は2択です。よって、A問題より楽です。得点配分は知りませんが。まず選択肢を見て5つに分けます。例えば選択肢の1をみると、分子にλがあって分母にπがあります。これに似ているのは、8のλ/πです。したがって、1と8は仲間です。これと同じように仲間を作ると、2と5、3と6、4と9、7と10となります。
　それでは問題に入ります。□アからいきます。こういう式を選ぶ問題は次元を調べます。選択肢の中で、単位が[V]になるのは、E[V/m]h_e[m]=[V]しかないです。したがって、□アは9です。

　□イは出来てください。
有効電力（アンテナが受信する最大の電力）

　Ｐ[W]（有効電力）　Ｅ[V/m]（電界）　l_e[m]（アンテナの実効長）　Ｒ_r[Ω]（放射抵抗）
　最低でも「分母が4」ってのは覚えてください。よって答えは5です。

　次に□ウです。実効高は単位が[m]なんで、選べるのは1か8しかないです。
半波長ダイポールアンテナの実効長

　l_e[m]（アンテナの実効長）　λ[m]（波長）
１／４接地アンテナの実効長

　l_e[m]（アンテナの実効長）　λ[m]（波長） 　とりあえず、半波長ダイポールアンテナの実効長はλ/π、1/4になると波長が半分なんだから実効高だって半分と覚えてください。これは、4アマでも出ます。だから覚えてください。よって答えは1です。

　次に□エはおいといて□オです。選べるのは7か10です。なんでか分かりますね。3と6は単位が[Ω]だから選べないです。選択肢を見てみると、分子に8があるか分母に4があるかです。どちらを選ぶべきかというと、感覚的に分母に8です。なぜなら選択肢を見ると皆、分母にばっかり数字がついてます。これをかけ算したら、どう考えても分子に4はきそうにないです。したがって、7を選びます。こんないい加減じゃやだと思ったら計算してみます。
　□イ=P=E²h_e²/4R_r

　　h_e(実効高)=λ/2π
　□イ=P=E²(λ/2π)²/4R_r
　□イ=P=E²λ²/16π²R_r
みると、分母に16とになってます。どーみても、分子が4になりそうにないです。したがって、7を選びます。
　そして□エですが、分母を8にするためには、3と6では3を選ぶ必要があります。したがって□エは3になります。

ア:9 イ:5 ウ:1 エ:3 オ:7

　まず選択肢をグループわけします。
　「導体損、回折損、誘電体損」「高次モード、基本モード」「導電率、誘電率」「磁気抵抗」「乾燥空気、圧縮空気」
　□アは「内壁表面に電流がながれ」とあります。内壁は金属で出来ているので発生するのは「導体損」です。
　□イは「減衰を少なくするため□イの大きい銀」とあります。銀に存在するパラメーターは導電率です。銀の誘電率なんて聞いたことないです。
　□ウのあとに「この損失」とあるので□ウには損失に関係あるものが来ます。損失で残っているものは回折損と誘電体損ですが、空気中に含まれている水分で回折がおこるとは考えられない（水滴くらい大きかったら考えられますが）ので誘電体損です。
　□エは水分を含んだらいけないので乾燥空気を注入すると考えるのが妥当でしょう。
　□オは基本モードです。導波管は高次モードは減衰が大きいので普通基本モードしか使いません。

ア:1 イ:4 ウ:5 エ:8 オ:9

B-3　次の記述は、ターンスタイルアンテナについて述べたものである。□内に入れるべき字句を下の番号から選べ。ただし、図に示すように、半波長ダイポールアンテナからθ方向の一定距離の点Pにおける電界強度eは、アンテナに流れる電流の最大値Iを、角周波数をω及び定数をｋとすれば、次式で表されるものとする。
　e=kIsinωtsinθ

(1)　二つの半波長ダイポールアンテナを中心で直交して互いに□ア度の位相差をもつ振幅の等しい電流で砺振し、二つの半波長ダイポールアンテナを含む面を水平にして水平方向の□イ偏波の電波を放射する。
(2)　直交した二つの半波長ダイポールアンテナを含む平面上の点Pにおける合成電界の強度e_tは、それぞれのアンテナの電界強度をe₁及びe₂とすれば次式となる。
e_t=e₁+e₂
=kIsinωtsinθ+□ウ
=kI(sinωtsinθ+cosωtcosθ)
=kIcos(ωt-θ)
(3)　上式より、合成電界の最大値の方向は角速度ωで回転し、電界の最大振幅kIは、二つの半波長ダイポールアンテナを含む平面上で一定であるので、指向性は水平面でほぼ□エとなる。
(4)　利得を増加するには、このターンスタイルアンテナを垂直方向に必要な段数を重ねて配置し、格段を□オで砺振する。
1　90　2　単一指向性　3　水平　4　180　5　kIsin(ωt+π/4)sin(π/4-θ)　6　垂直　7　同相　8　無指向性　9　逆相　10　kIsin(ωt+π/2)sin(π/2-θ)

　まずグループわけです。
　「90、180」「単一指向性、無指向性」「水平、垂直」「kIsin(ωt+π/4)sin(π/4-θ)、kIsin(ωt+π/2)sin(π/2-θ)」「同相、逆相」
　□アですが、角度を聞かれたら90度です。よってアは90です。
　□イですが、水平にしたら水平偏波しかでるわけないです。よって、イは水平です。
　□ウですが、式の違いはπ/2かπ/4かです。□アで90度を選んでいます。したがってπ/2を選ぶのが妥当です。よって、ウはπ/2のほうです。
　□エですが、「最大振幅は平面上で一定」とあるので、無指向性に決まってます。よってエは無指向性です。
　□オですが、格段を逆相で砺振したら打ち消しあってしまうので同相に決まってます。逆相で砺振することはないです。したがって□オは同相です。

ア:1 イ:3 ウ:10 エ:8 オ:7

　ちなみに、ターンスタイルアンテナはこんなやつです。
ターンスタイルアンテナとスーパーターンスタイルアンテナ

上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B　東京電気大学出版局　1992　の117ページより抜粋しています。
　左がターンスタイルアンテナ、右がスーパーターンスタイルアンテナです。

　まずグループわけです。
　「散乱、回折」「誘電率、導電率」「山岳、大地」「均一、不均一」「損失、利得」
　□アは散乱と回折で迷うところです。しかし(3)の文章で「散乱を起こして見通し外の遠方まで伝搬することがある」とあります。「伝搬することがある」ということは伝搬しないこともあるということです。ということで、確実に電波が届くのは回折波とわかります。よって□アは回折です。
　□イは山の話をしているので「山岳」です。
　□ウは増加するというのですから「利得」です。
　□エは不均一に決まってます。均一だったら怖いです。
　□オは大気といったら誘電率です。導電率が関係あるのは導体の時だけです。

ア:6 イ:3 ウ:10 エ:9 オ:2

まず答えを
ア:1 イ:2 ウ:2 エ:2 オ:1

　この問題は私にはよく分からないので分かるものだけ説明します。
　ウはどう考えても間違いです。最大放射方向とちょっとずれたところにサイドローブで大きいのがあったら前後じゃなくなってしまいます。前後なんですから、最大放射方向とその後ろ側の比と考えるのが適当でしょう。
　エは知っていれば間違いだと分かります。式も覚えてください。

開口面アンテナの測定距離の最小距離(誤差2%程度)

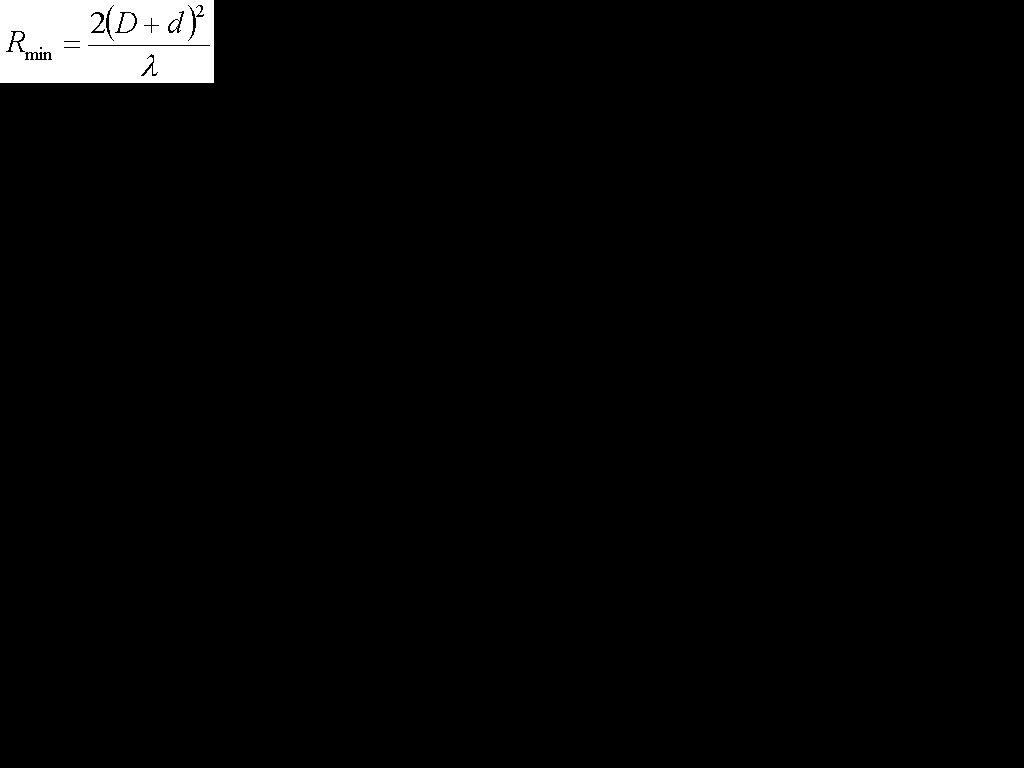
　R_min[m]（最小距離）　D[m](アンテナの直径)　d[m](アンテナの直径)　λ[m](波長)

　オは別に最大値を零デシベルとしても問題ない気がするのであっていると考えられます。
　以上、超いい加減ですが勘弁してください。
　イはケルビンブリッジではなくアドミタンスブリッジが使用されるそうです。