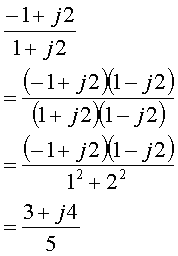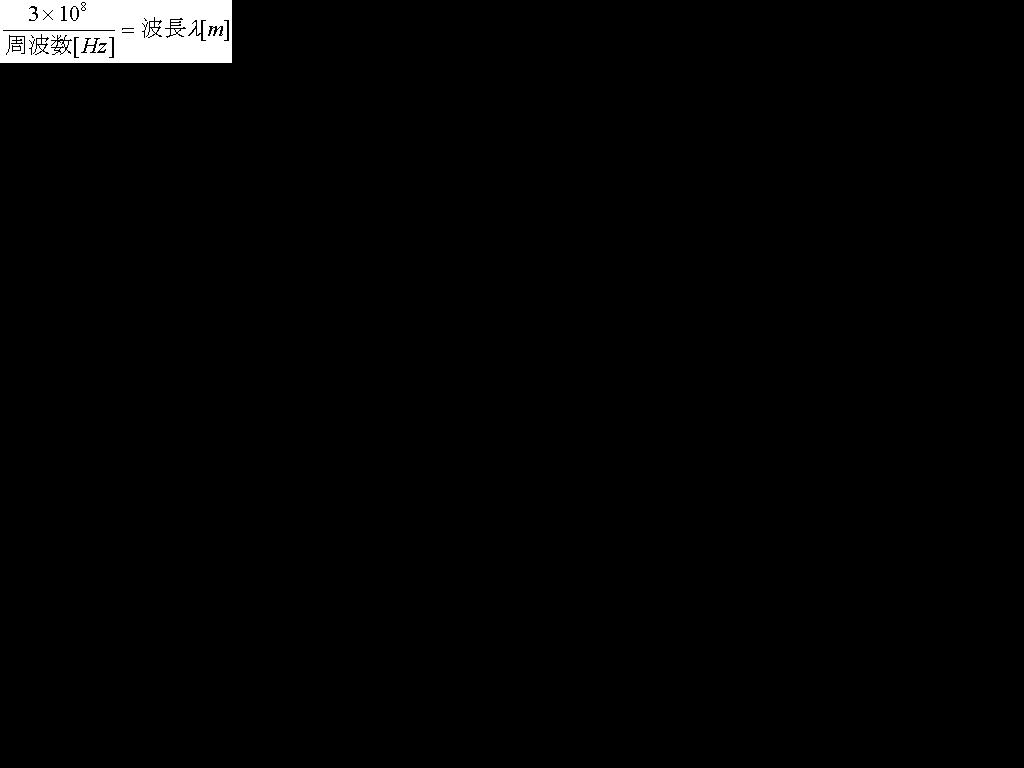
例えば3[GHz]の電波の波長はいくらかといった場合は、3×108/3×109=0.1[m]となります。
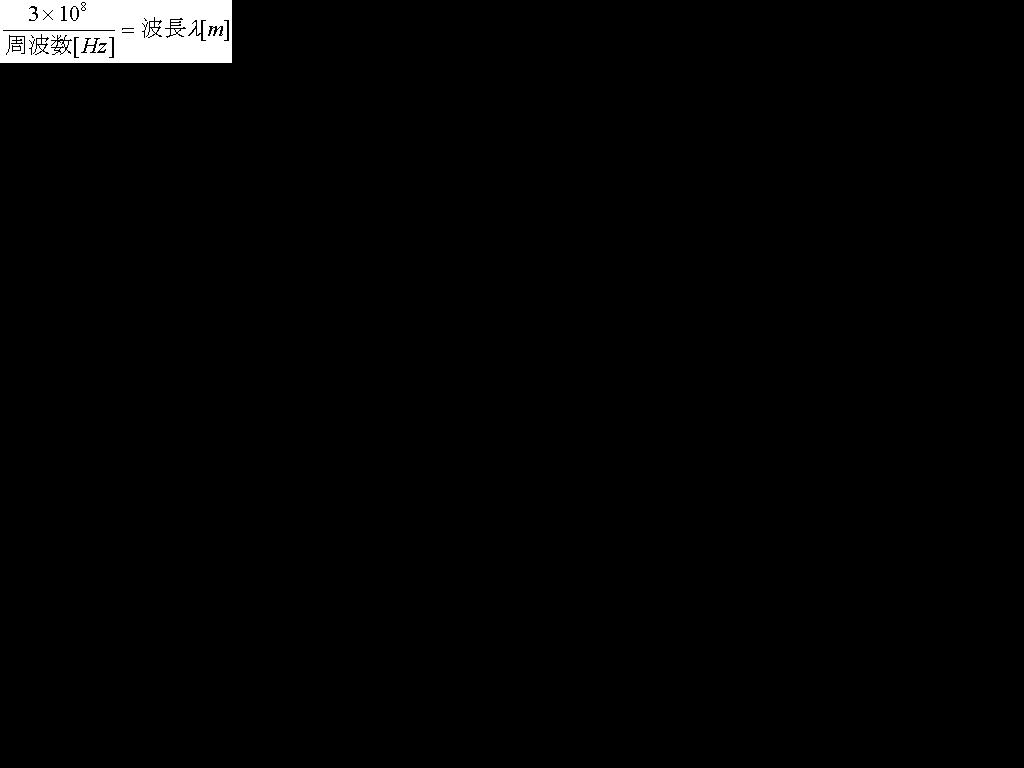
例えば3[GHz]の電波の波長はいくらかといった場合は、3×108/3×109=0.1[m]となります。
まず覚えてください。
log2=0.3
log3=0.4771
log5=0.7
log10=1
次にlogの後についている数字の指数はlogの前に出すことが出来ます。実例見れば分かります。
log102=2log10=2×1=2
log103=3log10=3×1=3
log10x=xlog10=x×1=x
log4=log22=2log2=2×0.3=0.6
log8=log23=3log2=3×0.3=0.9
ここまでは、logの数字を普通の数(真数といいます)になおしました。その反対はどうやるかです。
0.3=log2
0.47=log3
1=log10
x=log10x
これは暗記事項です。
ここからは実例見て学んでください。意味を説明するのめんどいんで(ぉい
1.47=1+0.47 1はlog10です。0.47はlog3です。 ここで10と3をかけて10×3=30です。
よって、1.47=log30です。
3.3=3+0.3 3はlog103です。0.3はlog2です。 ここで103と2をかけて103×2=2×103です。
よって、3.3=log2×103です。
最初の分解は、整数部分とそれ以外に分ければそれでおっけです。
あと単位によって真数とデシベルで表す数値の換算の仕方が違います。
G[dB]=10logG(真数)
P[dB]=10logP(真数)
E[dB]=20logE(真数)
Eの時にlogにかかる数字が20なので注意です。
例 電界強度80[dB](1[μV/m]を基準とした値)の電界はいくつでしょう?
E[dB]=20logE(真数)
80[dB]=20logE[μV/m]
4[dB]=logE[μV/m]
4[dB]=log104[μV/m]
よってE=104[μV/m]=10-2[V/m]
微小ダイポールの放射抵抗(重要)

R [Ω](放射抵抗) l [m](アンテナの長さ) λ [m](波長)
微小ダイポールアンテナの距離rにおける電界(覚えているとうれしい)

E [V/m](電界) r [m](距離)
この式自体は覚えないで、放射電磁界は距離rに反比例して誘導電磁界ってのは距離rの2乗に反比例するんだなってことと、距離rが大きいと誘導電磁界と静電界は距離の2乗とか3乗に比例するので無視していいことを覚えておけばおっけーです。
ポインチング電力(覚えているとうれしい)

W[W/m2](ポインチング電力) E [V/m](電界)
私は未だにボインチング電力ってのが何者か知りませんが、まあこの式だけはなんとなく覚えておいてください。
アンテナの実効面積などなど(重要)

Ae[m2](アンテナの実効面積) A [m2](アンテナの面積) λ [m](波長) G [単位なし](利得) η[単位なし](開口効率)
アンテナに誘起する電圧
![]()
V[V](電圧) E[V/m](電界) le[m](アンテナの実効長)
アンテナの近くに電界Eがあった時に、どのくらいの電圧がアンテナに誘起するか(電圧が誘起すると電流が流れるので電波が受信される)の式です。実効長はアンテナによって決まっています。最後についているsinθはアンテナに対してどんな角度で電波が入ってきているかな?という数値ですが、無線の試験では角度の計算はいらないのでsinθは忘れていいです。したがって覚えるべき公式は、
アンテナに誘起する電圧
![]()
V[V](電圧) E[V/m](電界) le[m](アンテナの実効長)
です。
受信機に誘起する電圧
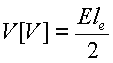
V[V](電圧) E[V/m](電界) le[m](アンテナの実効長)
2で割る理由は参考書で「有効電力」あたりを調べると載ってるでしょう。適当に説明しますと、アンテナの誘起電圧をV[V]、アンテナのインピーダンスがR1、受信機のインピーダンスがR2とすると、アンテナと受信機は直列に繋がっているので、R1にV/2[V]の電圧がかかって、R2にV/2[V]の電圧がかかるからです。
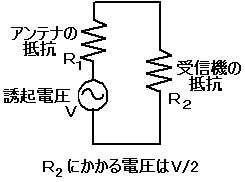
ちなみに、これは回路が整合してる時です。
有効電力(アンテナが受信する最大の電力)

P[W](有効電力) V[V](電圧) Rr[Ω](放射抵抗)
これに上のV=Eleを代入すると、
有効電力(アンテナが受信する最大の電力)

P[W](有効電力) E[V/m](電界) le[m](アンテナの実効長) Rr[Ω](放射抵抗)
半波長ダイポールアンテナの実効長

le[m](アンテナの実効長) λ[m](波長)
1/4接地アンテナの実効長

le[m](アンテナの実効長) λ[m](波長)
ループアンテナの実効高(覚えているとうれしい)
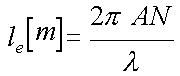
le[m](アンテナの実効長) λ[m](波長) A[m2](ループ面積) N[回](巻き数)
1/4波長整合回路
 のとき、
のとき、
Z0[Ω](特性インピーダンス) Zq[Ω](1/4波長整合回路の特性インピーダンス) R[Ω](負荷抵抗)
平行2線式給電線の特性インピーダンス
 のような平行2線式給電線の特性インピーダンスは、
のような平行2線式給電線の特性インピーダンスは、
Z0[Ω](特性インピーダンス) D[m](導線の間隔) d[m](導線の直径)
同軸線路の特性インピーダンス


Z0[Ω](特性インピーダンス) D[m](外部導体の内径) d[m](内部導体の外径) εr(比誘電率)
反射損

M[単位なし](反射損) S[単位なし](電圧定在波比)
地上高h1[m]のアンテナの見通し距離d(アンテナが1つの場合)1[km]

地上高h1[m]と地上高h2[m]のアンテナの幾何学的見通し距離d0[km]と電波の見通し距離d0'[km]
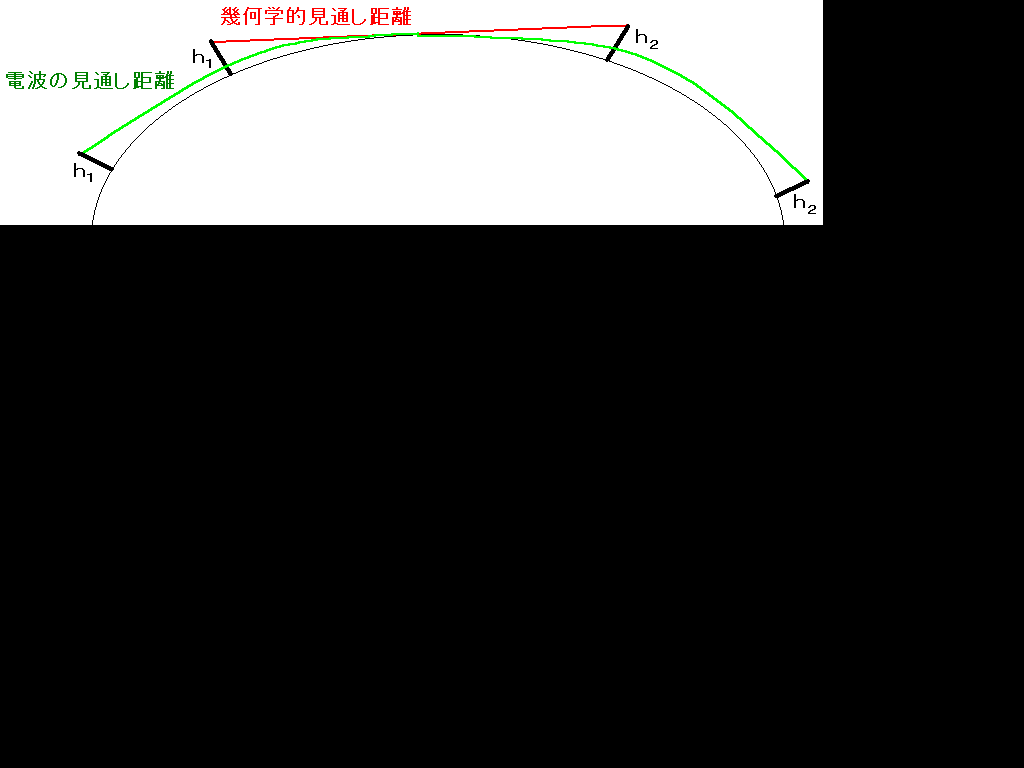
幾何学的見通し距離
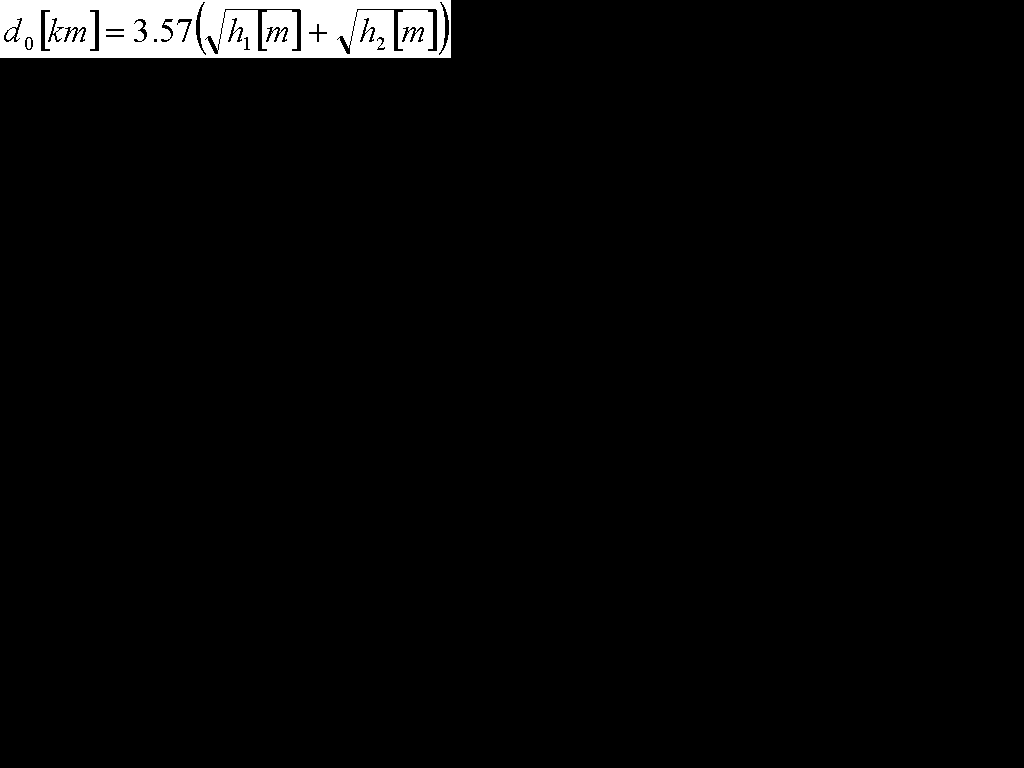
電波の見通し距離(電波は大気によって屈折するので遠くまで届きます。緑色の線です。)
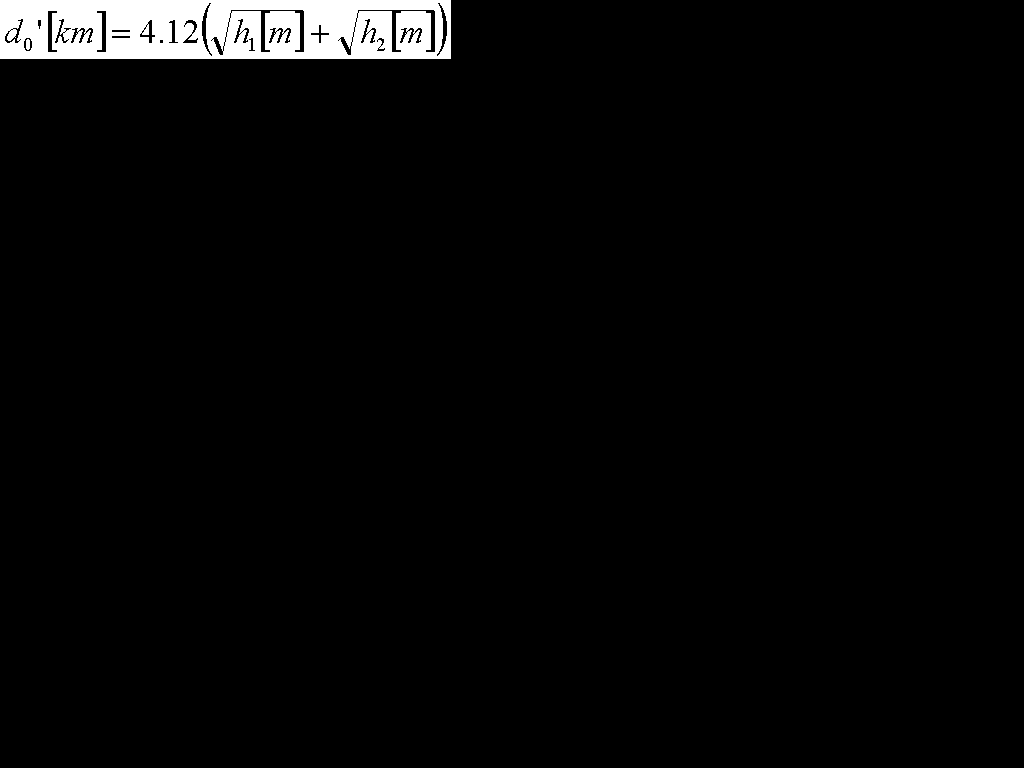
自由空間伝搬損失Γ
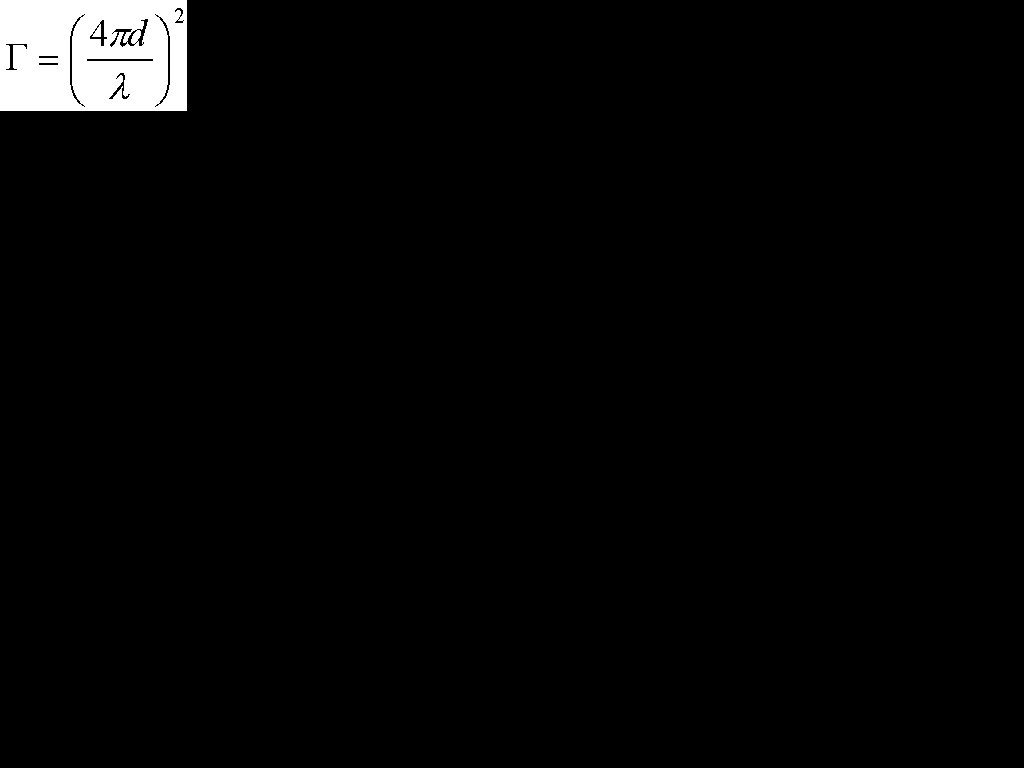
Γ[単位なし](自由空間伝搬損失) d[m](距離) λ[m](波長)
ΓはdBになおして使用することが多いです。その時は、10log10Γです。
この式を見て分かることは、伝搬損失は距離の2乗に比例して増えて(要するに距離が増えると損失は増える、当たり前だけど)、波長の2乗に反比例して損失は増える(要するに波長が長ければ長いほど損失が小さい)。
ところで、10logΓ=10log(4πd/λ) 2を計算するのは周波数から波長を求めたりπがあるので、3.14をかけ算したりと大変です。以下に示す近似式を使うと計算が楽かもしれません。お好みでお使い下さい。
Γ[dB]=32.4+20logf+20logd
f[MHz](周波数) d[km](距離)
この式は津本@愛知県さんに教えていただきました。
デシベル計算の場合
Ps[dB]=Pt[dB]+Gs[dB]+Gt[dB]-Γ[dB]
受信電力=送信電力+送信アンテナの利得+受信アンテナの利得-自由空間伝搬損失
真数計算の場合
Ps=Pt×Gs×Gt÷Γ
受信電力=送信電力×送信アンテナの利得×受信アンテナの利得÷自由空間伝搬損失
開口面アンテナの測定距離の最小距離(誤差2%程度)
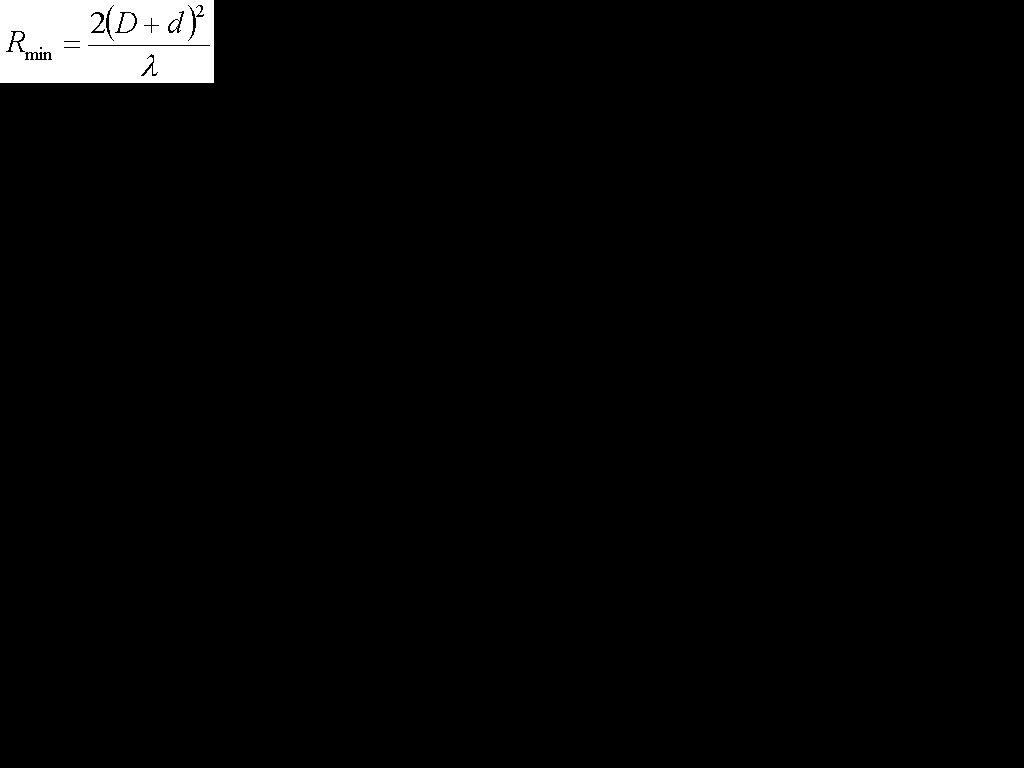
Rmin[m](最小距離) D[m](アンテナの直径) d[m](アンテナの直径) λ[m](波長)

Z0[Ω](特性インピーダンス) ZL[Ω](回路に繋がれている抵抗) V1[V](入射電圧) V2[V](反射電圧)
電圧定在波比と反射係数の定義(まあ重要)

S[単位なし](電圧定在波比) Γ[単位なし](反射係数)
電圧定在波比と反射係数の相互変換(重要)

S[単位なし](電圧定在波比) Γ[単位なし](反射係数)
マイクロアンテナの受信点の電力密度(重要)

W0[W/m2](電力密度) Pt[W](送信電力) Gt[単位なし](送信アンテナの絶対利得) d[m](送信アンテナからの距離)
アンテナ軸に垂直の方向(最大放射方向)に距離d[m]離れた点における電界強度
半波長ダイポールアンテナによる電界強度

E[V/m](受信電界強度) P[W](送信電力) d[m](送信アンテナからの距離)
微小ダイポールアンテナによる電界強度

E[V/m](受信電界強度) P[W](送信電力) d[m](送信アンテナからの距離)
等方性アンテナによる電界強度

E[V/m](受信電界強度) P[W](送信電力) d[m](送信アンテナからの距離)
λ/4接地アンテナによる電界強度

E[V/m](受信電界強度) P[W](送信電力) d[m](送信アンテナからの距離)
絶対利得GIのアンテナによる電界強度

E[V/m](受信電界強度) P[W](送信電力) d[m](送信アンテナからの距離)
相対利得Gのアンテナによる電界強度

E[V/m](受信電界強度) P[W](送信電力) d[m](送信アンテナからの距離)
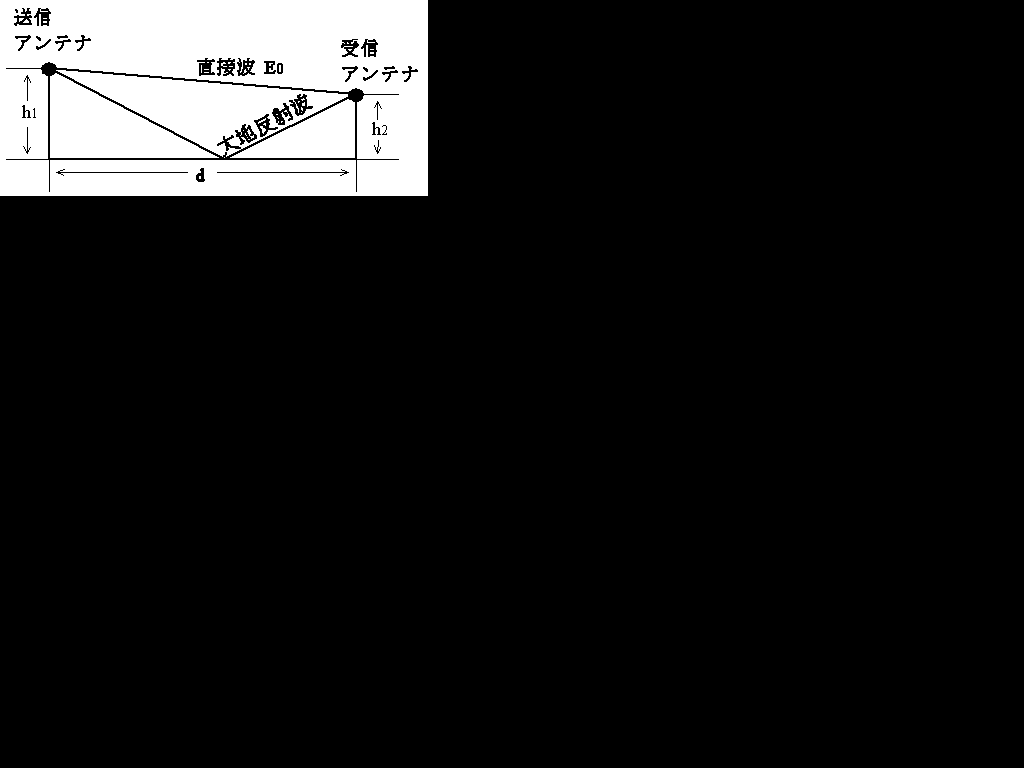
直接波と大地反射波の合成

E[V/m](合成波の受信電界強度) E0[V/m](直接波の受信電界強度) h1[m](送信アンテナの高さ) h2[m](受信アンテナの高さ) λ[m](波長) d[m](距離)
もし、 の時は
の時は
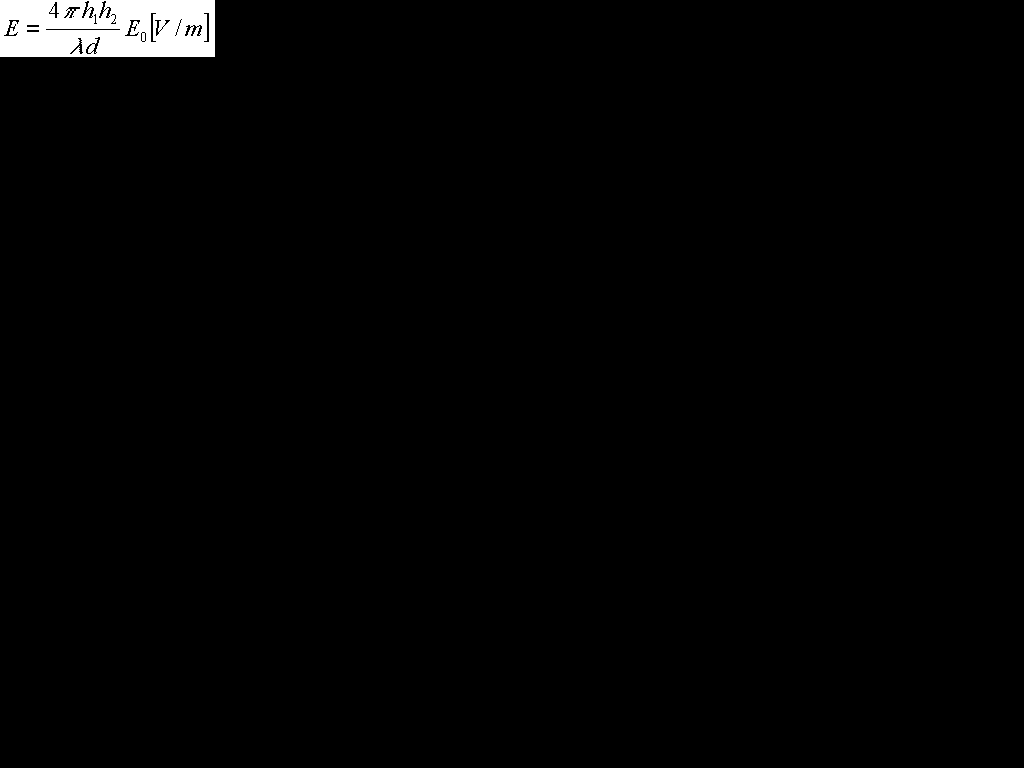
E[V/m](合成波の受信電界強度) E0[V/m](直接波の受信電界強度) h1[m](送信アンテナの高さ) h2[m](受信アンテナの高さ) λ[m](波長) d[m](距離)
最高周波数×0.85=最適周波数
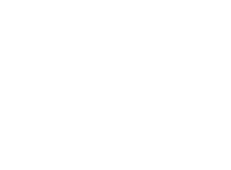
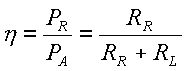
η(放射効率) PA[W](アンテナへの入射電力) PR[W](アンテナの放射電力) RR[Ω](アンテナの放射抵抗) RL[Ω](損失抵抗)
ρ=λ/1000の半波長ダイポールアンテナの放射リアクタンスのグラフ
ρ[m](素子の直径)、λ[m](波長)
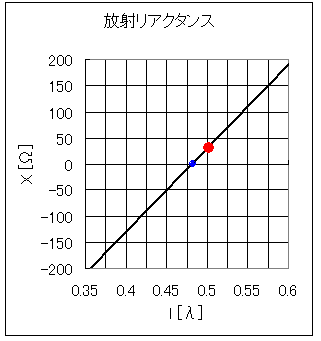
半波長のアンテナですと、l=0.5[λ]なので放射リアクタンスは赤い点のところでリアクタンスXは42.55[Ω]になります。このリアクタンスは整合をとる際に邪魔なのでリアクタンスを消すためにアンテナを半波長よりちょっと短くしてあげます。青い点のところだとXが0[Ω]になります。だいたいl=0.475[λ]あたりです。ρ=λ/1000の半波長ダイポールアンテナの場合、アンテナを半波長より0.025[λ]だけ短くしてあげるとXが0になって整合回路が楽に作れるようになります。
アンテナが半波長より長いとX[Ω]の値は大きくなります。X[Ω]の値が正の値をとるとき、X[Ω]のことを誘導性リアクタンスといいます。アンテナが半波長より短いとX[Ω]の値は小さくなります。X[Ω]の値が負の値をとるとき、X[Ω]のことを容量性リアクタンスといいます。
ところで、抵抗とコイルとコンデンサが直列になってる回路のインピーダンスは下のような式で表されます。
_________
Z = √R^2 + (XL - XC)^2
Z : インピーダンス
R : 抵抗
XL : 誘導性リアクタンス
XC : 容量性リアクタンス
X[Ω]が正の値の時は、この式のXLにあたります。要するにX[Ω]が誘導性リアクタンスのときはコイルな感じです。X[Ω]が負の値の時は、この式のXCにあたります。要するにX[Ω]が容量性リアクタンスのときはコンデンサな感じです。
ちなみに、私は「あ、コイルってのは電気を進ませそうな感じがするから誘導性、コンデンサは電気をせきとめそうな気がするから容量性」と覚えてます。
微小ダイポールアンテナの実効面積
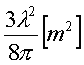
λ[m](波長)
半波長ダイポールアンテナの放射抵抗 73.13[Ω]
位相定数β
β=2π/λ
導波管の遮断波長
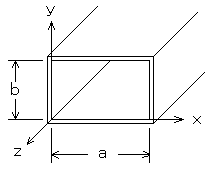
遮断波長= 2a[m]
位相速度と群速度では群速度の方が遅い
導波管の分岐の様子(分岐する方向)
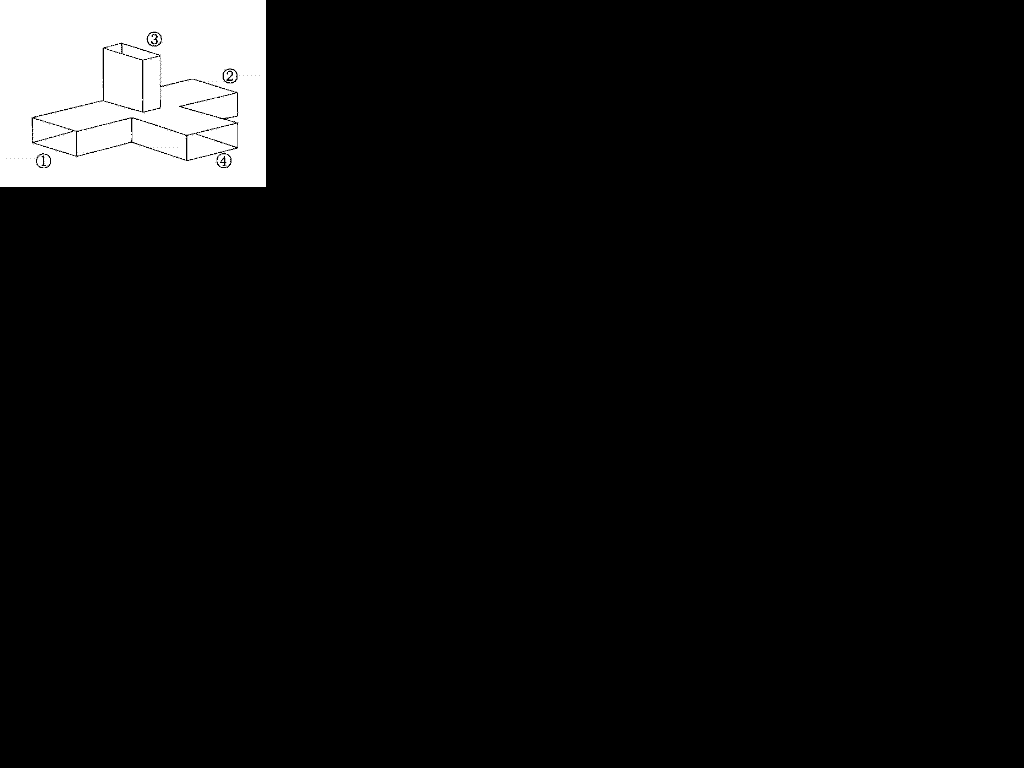
○3から入った波は長方形の向きが同じである○1と○2にぬけます。
○4から入った波は長方形の向きが同じである○2と○1にぬけます。
導波管の分岐の様子(位相)
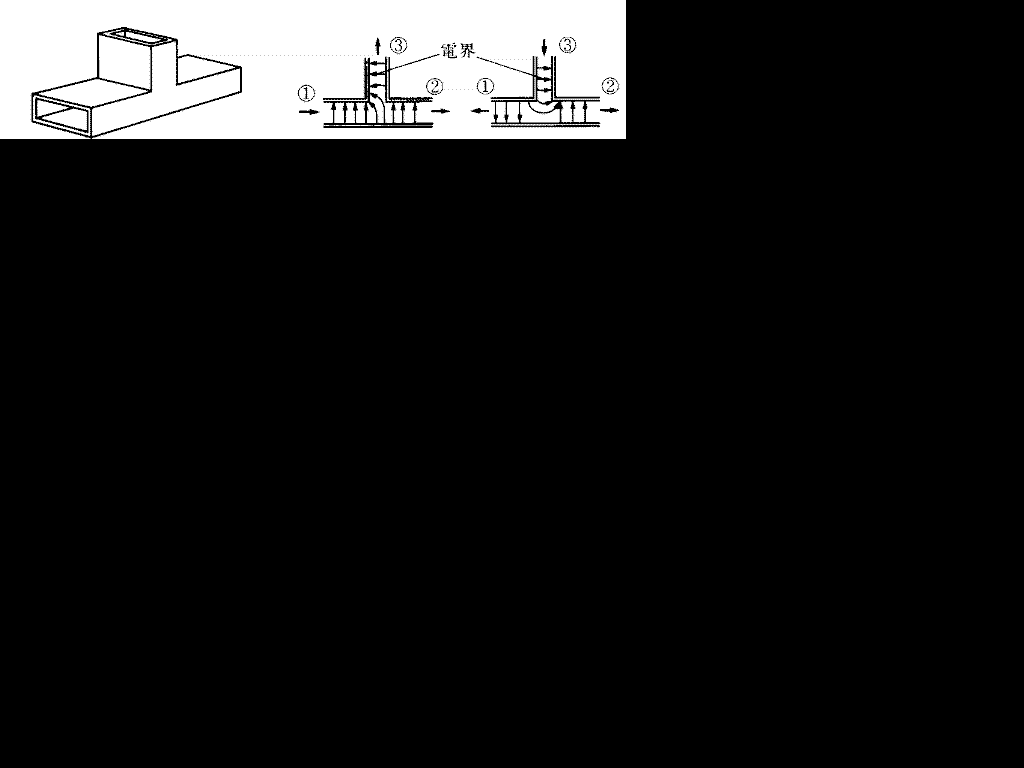
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B 東京電気大学出版局 1992 の32ページより抜粋しています。
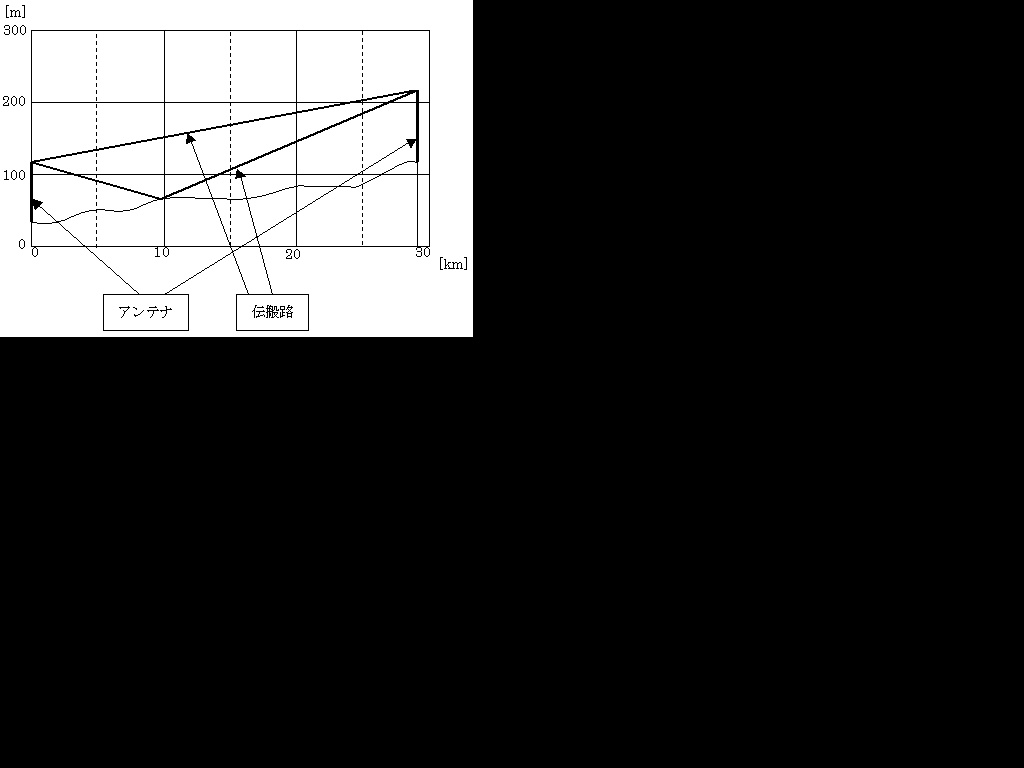
直接波が山岳などのナイフのようにとがった障害物にあたると回折してしまって受信点では回折波と直接波が干渉を起こします。そこで、回折が起こらないように第一フレネルゾーンに障害物が入らないようにします。
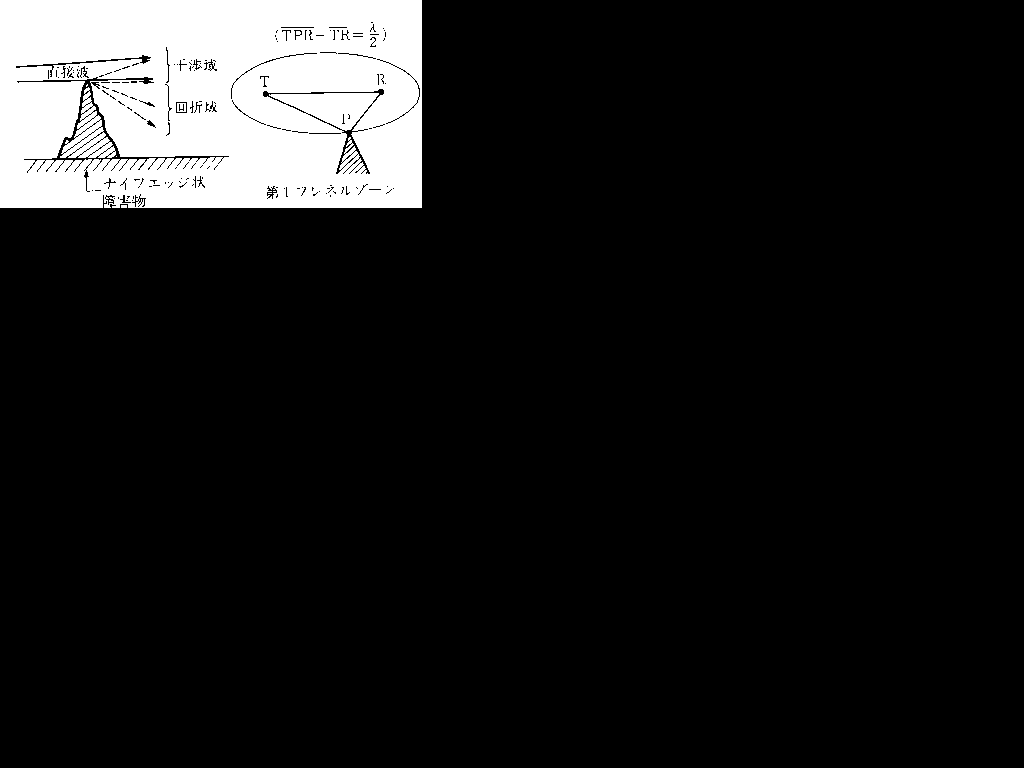
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B 東京電気大学出版局 1992 の158ページより抜粋しています。
電波が第一フレネルゾーンに入らないようにすることをクリアランスをとると言います。
もしかしたら、第一フレネルゾーンを求める計算が出るかもしんない(昔は出てた)ので、式も覚えておくとうれしいかもしんないです。第一フレネルゾーンは楕円形をしています。焦点2つありますので。
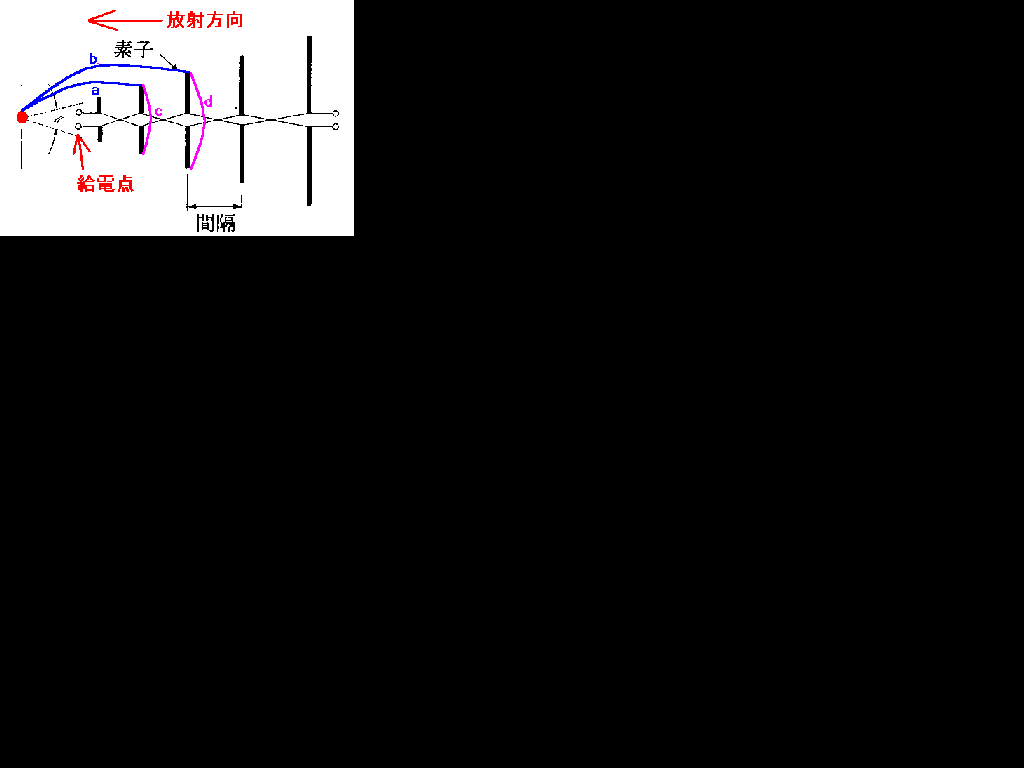
隣り合うダイポールの長さの比が、ダイポール列の先端を結ぶ頂点からそのダイポールまでの位置までの距離に等しい。要するに、b/a=d/c。
使用可能な周波数の下限は、最も長いダイポールの長さが1/2波長となる周波数。
使用可能な周波数の上限は、最も短いダイポールの長さが1/2波長となる周波数。
周波数帯域は1:10程度。
入力インピーダンスや放射特性などが、周波数の対数に比例して周期的に繰り返す構造。
バックファイヤアンテナなので、給電点方向に向かって電波が放射される。
利得は数デシベル。
バラン
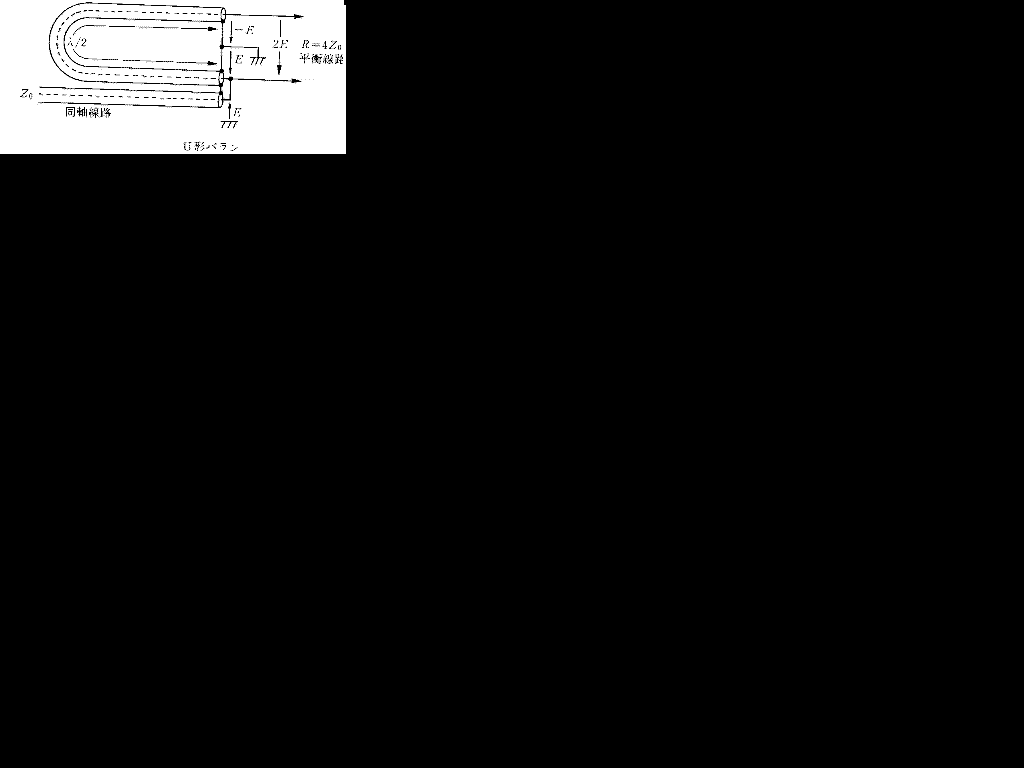
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B 東京電気大学出版局 1992 の21ページより抜粋しています。
スタブ
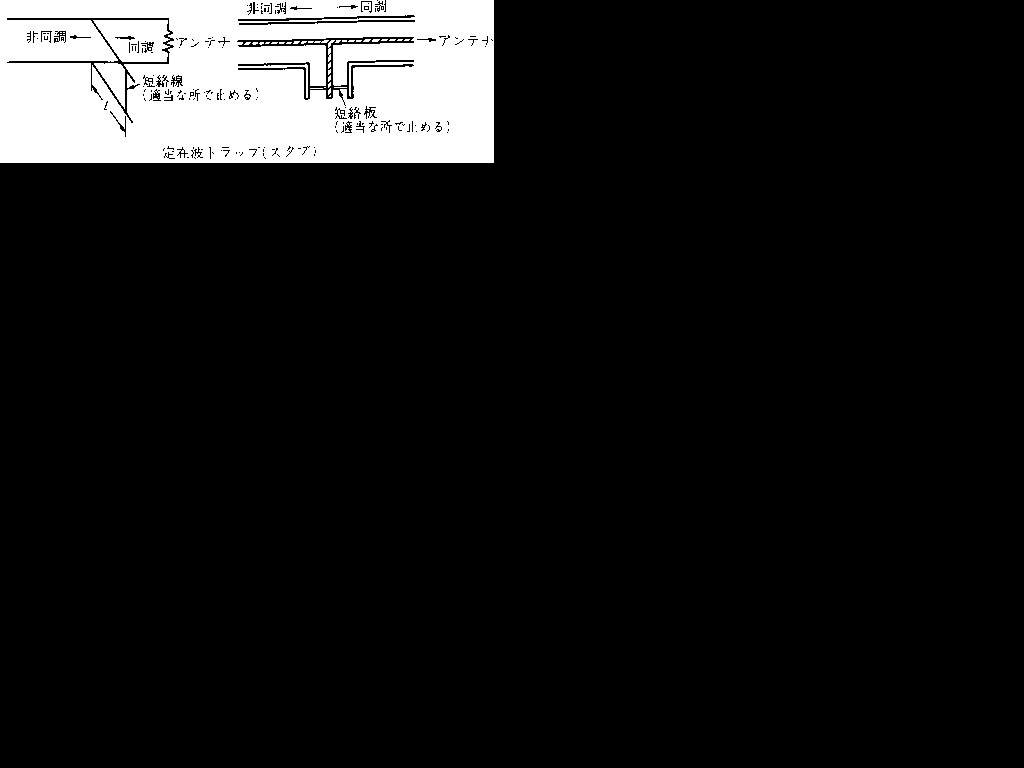
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B 東京電気大学出版局 1992 の19ページより抜粋しています。
スリーブアンテナ

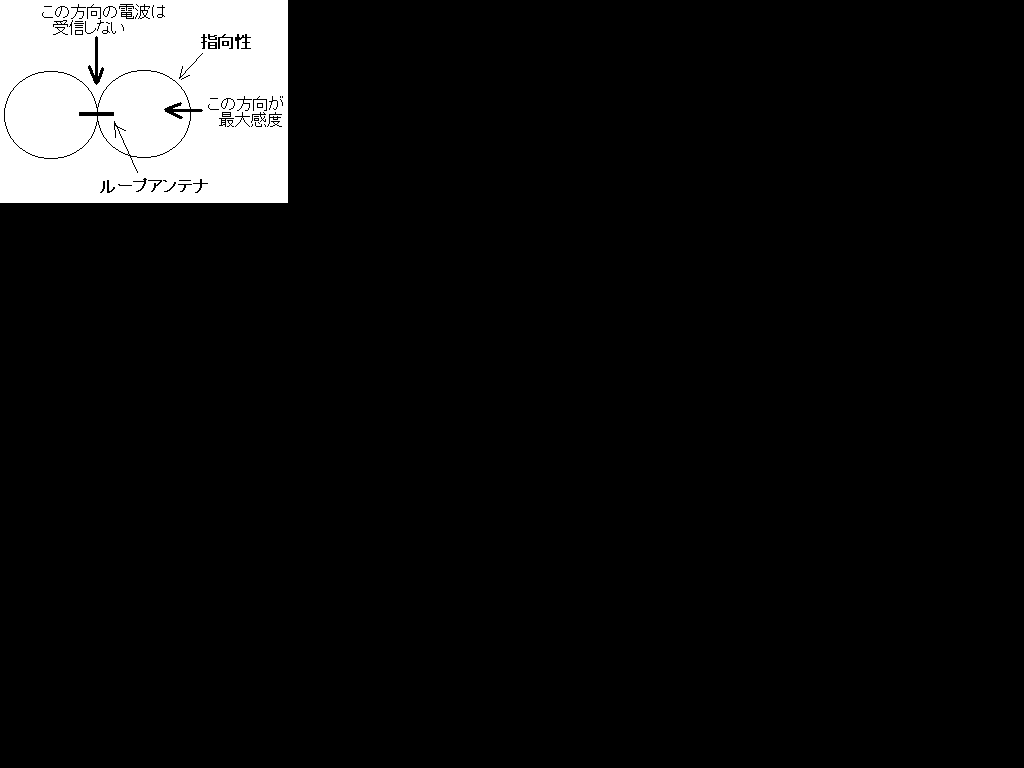
ループアンテナの指向性(水平面)
ターンスタイルアンテナとスーパーターンスタイルアンテナ

上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B 東京電気大学出版局 1992 の117ページより抜粋しています。
左がターンスタイルアンテナ、右がスーパーターンスタイルアンテナです。
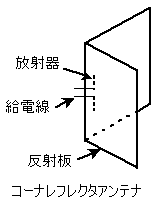
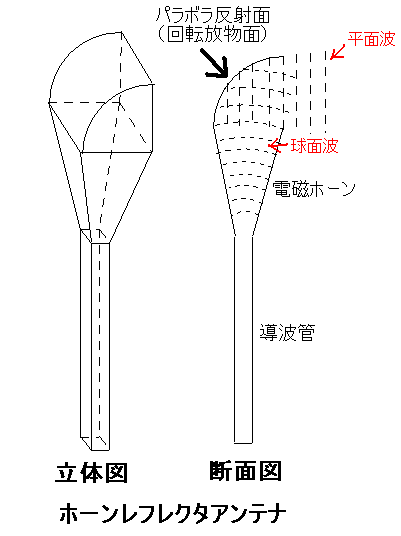
サイドローブが小さい。開口効率が大きい。直線偏波、円偏波に使用できる。
水平面
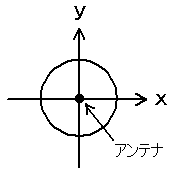
垂直面
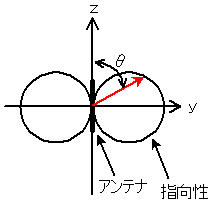
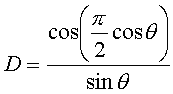
D(指向性)、θ[rad](アンテナの軸からの角度)
折り返しダイポールアンテナ

メインローブとサイドローブとバックローブ
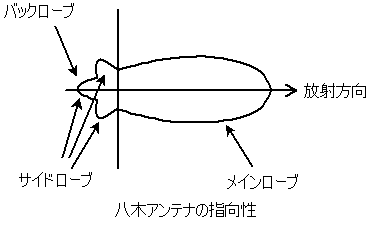
目的の方向への放射ビームで最大のものをメインローブ、それとは反対の方向に生じる不要な放射をサイドローブ、サイドローブの中で最大のものをバックローブと呼ぶ。
メインローブとバックローブとの比をとったものをFB(Front/Back)比と言い、デシベル(dB)で表示する。
FB=20log(メインローブ最大値/バックローブ最大値)
フリスの伝達公式の使い方(重要)

まず上の図のような構成を考えます。アンテナ(利得なし)から送信電力Ptで電波を出すと距離dの位置での電力密度W[W/m2]はPt/4πd 2です。
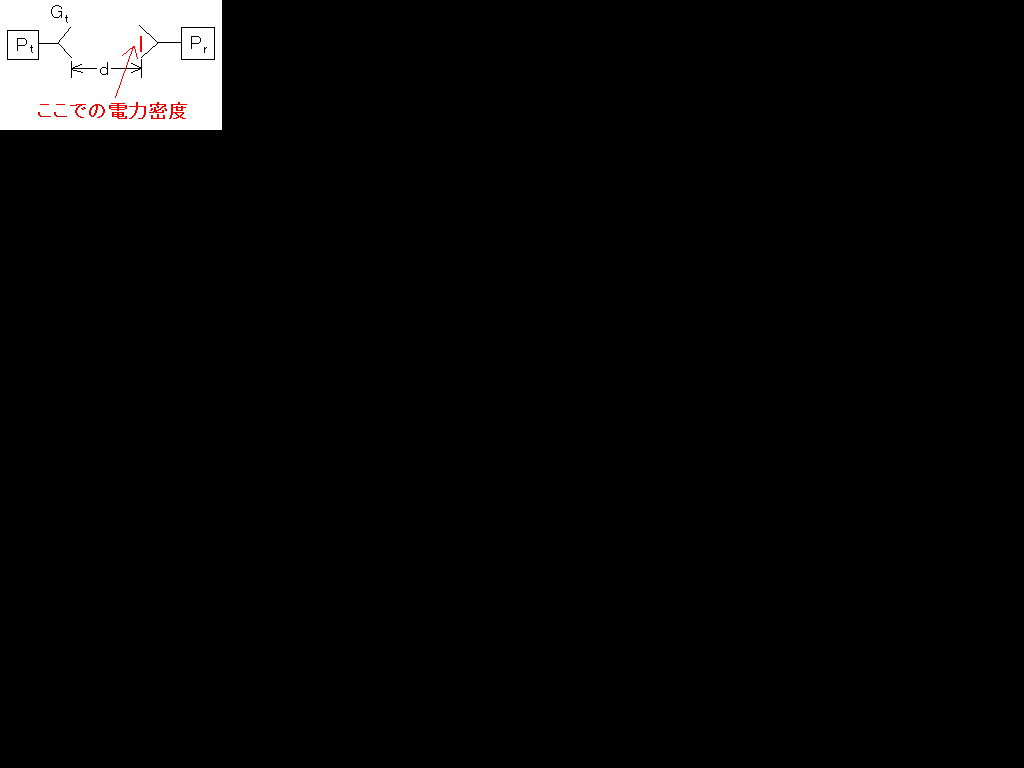
次に、アンテナに利得がGtあったとします。すると距離dの位置での電力密度W[W/m2]はPtGt/4πd 2です。
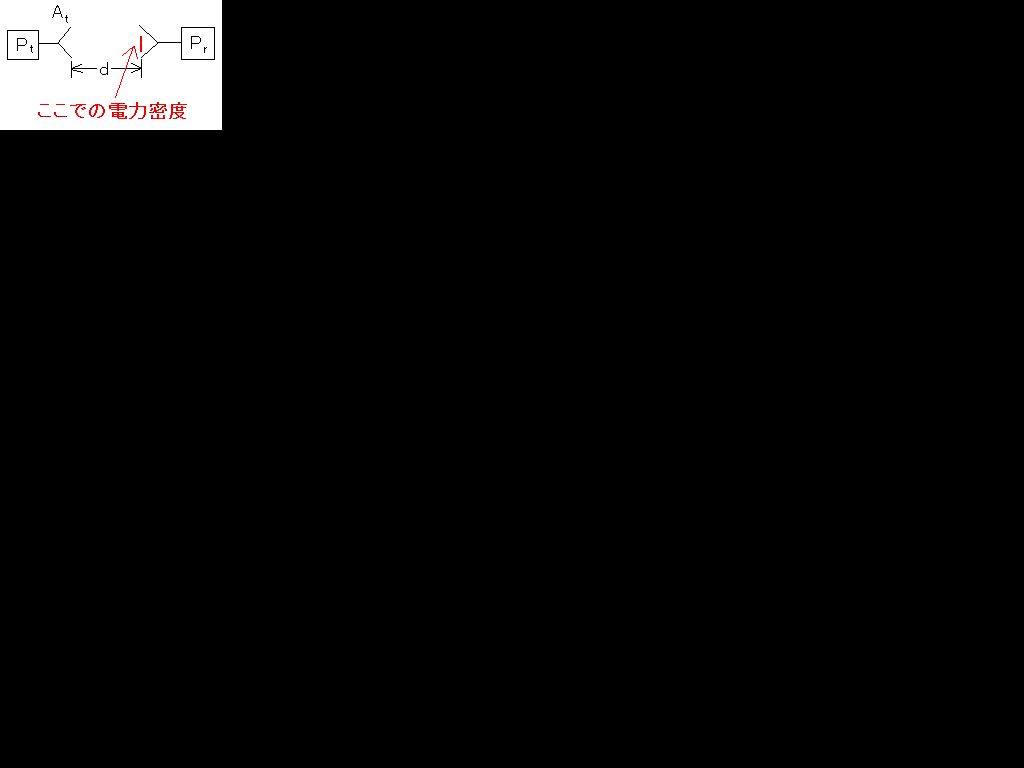
利得がGtではなくて、実効面積Atが与えられた場合は、まずAe=λ2G/4πを思い出します。これをG=の式になおすと、G=4πAe/λ2。これをPtGt/4πd 2のGtに代入すると、電力密度W[W/m2]はAtPt/λ2d 2です。

今度は送信アンテナの利得がGt、受信アンテナの実効面積がArだったとします。Pr(受信電力)[W]=W(電力密度)[W/m2]×Ar(実効面積)[m2]です。W[W/m2]はPtGt/4πd 2なので、Pr(受信電力)[W]=PtGtAr/4πd 2です。

それでは、送信アンテナの利得がGt、受信アンテナの利得がGrだったとすると、Pr(受信電力)[W]=PtGtAr/4πd 2のArにAe=λ2G/4πを代入するだけです。結果、Pr(受信電力)[W]=λ2PtGtGr/(4πd)2となります。この式はよく見ます。
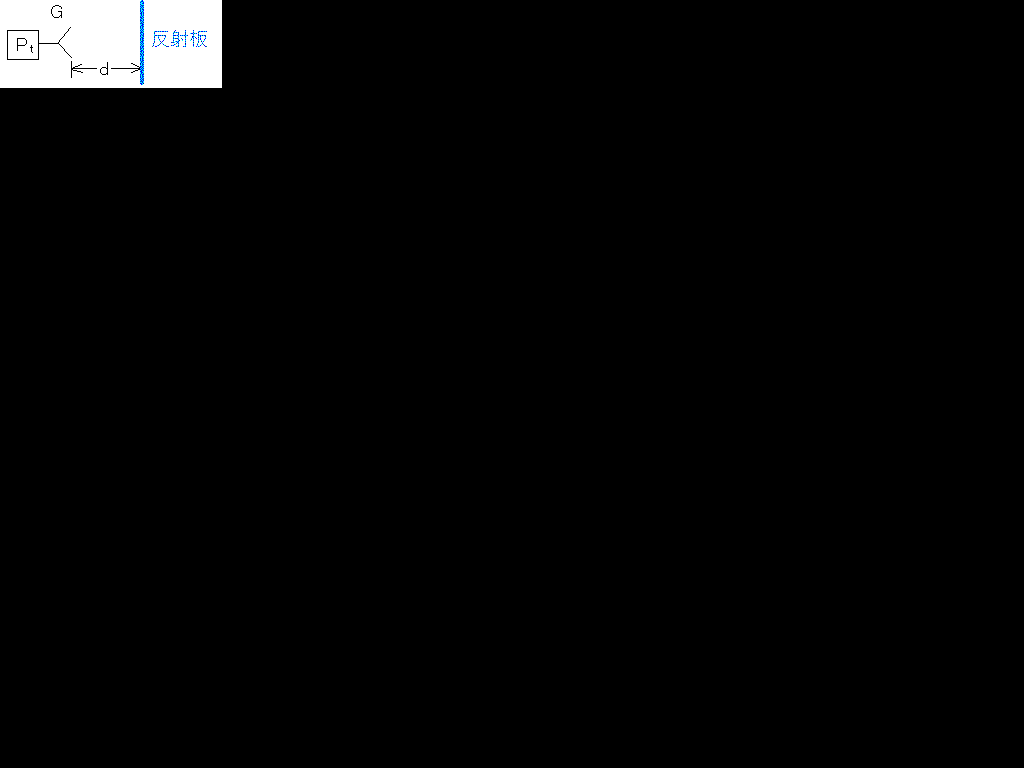
ときどき、上の図のように受信アンテナと送信アンテナを共用して利得を計算したりする問題が出ます。この場合は、送信利得、受信利得が共にG、距離を2dとして上の式にいれればいいので、Pr(受信電力)[W]=λ2PtG2/(4π(2d))2=λ2PtG2/(16πd)2となります。利得が知りたかったら、この式をG=になおせばよいです。
絶対利得とは等方性アンテナを基準とした任意のアンテナの利得です。
相対利得とは半波長ダイポールアンテナを基準とした任意のアンテナの利得です。
半波長ダイポールアンテナの絶対利得は1.64(2.15[dB])です。当たり前ですけど、半波長ダイポールアンテナの相対利得は0[dB]です。
指向性利得とはあるアンテナから電波が全方向へ均等に放射されたとしたときの放射強度に対する特定方向への放射強度の比です。
指向性利得×アンテナ効率(<1)=絶対利得

| 相対利得 | 絶対利得 | 指向性利得 | |
|---|---|---|---|
| 半波長ダイポールアンテナ | 0[dB] | 2.15[dB] | 2.15[dB] |
| 等方性アンテナ | -2.15[dB] | 0[dB] | 0[dB] |
| アンテナ効率が0.8で相対利得が10[dB]のアンテナ | 10[dB] | 12.15[dB] | 13.1[dB] |
短縮率
半波長ダイポールアンテナはZ≒73.1+j42.6のように放射抵抗以外に放射リアクタンスを持ちます。このリアクタンス成分があると、給電する場合に整合回路が複雑になります(純抵抗だけだったら抵抗だけ考えて整合とればいいですけど、リアクタンスが入っていると抵抗とリアクタンスの両方を考えて整合を取らないとダメなのでめんどくさそうです)。
アンテナを少し短くすると放射リアクタンスが零になる点が存在します。この短くする割合を短縮率といいます。
なんで短くすると放射リアクタンスが零になるかは、難しい本を読んでください。
高さは100km。夏に出る。黒点の影響は受けない。超短波をよく反射。
ちなみに、電離層は下からD層、E層、F層の順番です。
定在波アンテナ(高調波アンテナ)
使用する波長に比べて長い導体(半波長アンテナよりも長い導体長で使用する)を放射体として使用するアンテナで、アンテナ導体の終端は開放であるため、定在波がのる。
分母が複素数だった場合の計算方法
分母が複素数である式を計算する時は、分母に共役複素数をかけて、分母から虚数を消してから計算する必要があります。共役複素数という言葉は覚えなくていいので、計算方法だけ覚えてください。
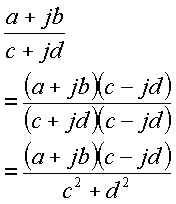
次に具体例を示します。