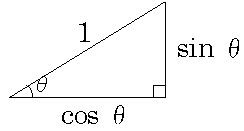
斜辺が1である右下に直角があって左下の角の角度がθ(シータと読みます)の三角形の下の辺の長さをcosθ、右の辺の長さをsinθと定義します。これはθが左下にあった場合です、じゃあ右上にθがあった場合はどうなるかと言うと、
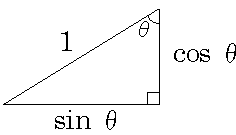
となります。ややこしいので、上の図で覚えた方がいいでしょう。
結論から言います。以下の図をご覧下さい。
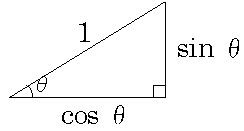
斜辺が1である右下に直角があって左下の角の角度がθ(シータと読みます)の三角形の下の辺の長さをcosθ、右の辺の長さをsinθと定義します。これはθが左下にあった場合です、じゃあ右上にθがあった場合はどうなるかと言うと、
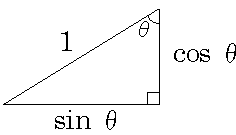
となります。ややこしいので、上の図で覚えた方がいいでしょう。
具体的な値の求め方に行きます。
θが30度の時、sinθとcosθいくつになるでしょうか?
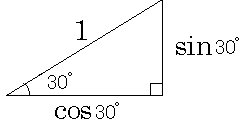
この三角形は資格試験によく出る、っていうか、これしか普通は出ないぞ、っていう三角形の2番目の三角形と相似です。相似な三角形は対応する辺の比が一緒です。二つの三角形を並べてみましょう。
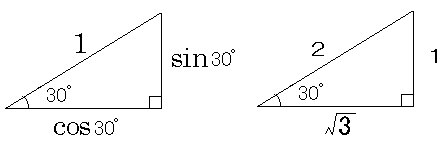
右の三角形で2のところが、左の三角形では1です。したがって、右の三角形を1/2にしたものが、左の三角形です。
よって、sin30゜は1/2、cos30゜は(ルート3)/2です。
θが60度の時、sinθとcosθいくつになるでしょうか?
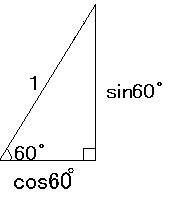
この三角形はやっぱり資格試験によく出る、っていうか、これしか普通は出ないぞ、っていう三角形の2番目の三角形と相似です。相似な三角形は対応する辺の比が一緒です。二つの三角形を並べてみましょう。
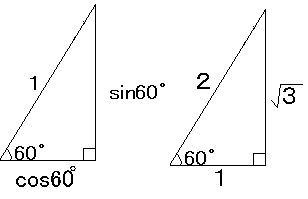
右の三角形で2のところが、左の三角形では1です。したがって、右の三角形を1/2にしたものが、左の三角形です。
よって、sin60゜は(ルート3)/2、cos30゜は1/2です。
θが45度の時、sinθとcosθいくつになるでしょうか?
そろそろ面倒なので、最初から対比させときます。
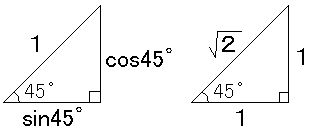
右の三角形でルート2のところが、左の三角形では1です。したがって、右の三角形を1/(ルート2)にしたものが、左の三角形です。
よって、sin45゜もcos45゜も1/(ルート2)です。
では、ここまで分かった事を表にして見ましょう。
| 30゜ | 45゜ | 60゜ | |
|---|---|---|---|
| sin | |||
| cos |
この表は覚える必要はないです。cos30゜とかが知りたくなったら、実際に三角形を書いてみます。短い辺は1/2、長い辺は2/(ルート3)、45゜の時は1/(ルート2)と覚えておけばおっけーだと思います。
私の場合は以下の用に思考します(cos30゜の場合)。ちなみにこの考え方が、三角関数の本当の考え方だと思いました。
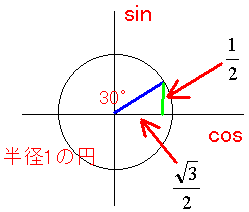
まず横はcos、縦はsinです。これは暗記。適当に座標を書いて半径1らしき円を書きます。この場合は30゜のcosθの値を知りたいので中心から30゜の角度(適当です)で線(青い線です)をひっぱって、円にあたったら、そっから垂直にx軸まで線(緑の線です)を引きます。
出来た三角形を見て、ああcos30゜は(ルート3)/2だな、と判断します。三角形の長い辺は(ルート3)/2です。
1/2と(ルート3)/2という数は当然暗記です。
おわかり頂けるでしょうか・・・
あとsinとcosで覚える事柄は角度が0゜又は90゜の時です。
sin0゜は0、cos0゜は1です。上で説明した円を書くやり方で説明します。
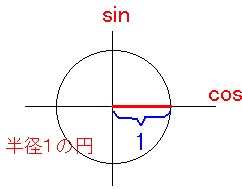
0゜で線を引くと図のようになります。cosの方向に長さが1の線を引くことになります(赤い線)。したがって、cos0゜は1です。でも、sinの方向には線がないですよね。だから、sin0゜は0です。
おわかり頂けるでしょうか・・・
90゜の時は面倒なので書きませんが、sinの方向に長さが1の線を引くことになるので、sin90゜は1、cos90゜は0になります。
| 0゜ | 30゜ | 45゜ | 60゜ | 90゜ | |
|---|---|---|---|---|---|
| sin | 0 | 1 | |||
| cos | 1 | 0 |
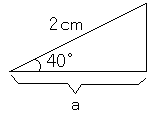
cos40゜が0.64ということは、要するに下の図です。
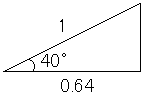
問題の三角形の斜辺は2cmなので、0.64を2倍して、答えは1.28cmです。
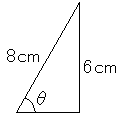
sinとかcosは斜辺が1の三角形を基準にしています。そこで、斜辺を1cmに縮小してみます。すると下図のようになります。
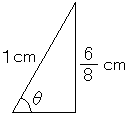
従って、sinθは6/8=3/4です。
重要 要するにこれが分かっていればおっけー
sinθとcosθの公式は以下のようになっています。
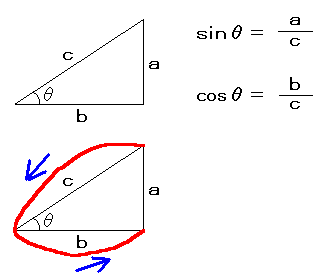
覚え方はcosθの場合、上の図の下を見てください。赤い線でCを書いているつもりなんですが、順番に分母、分子になります。
ああ、言ってることがわかんないですね。Cを書こうとすると最初にcを通りますよね、だからcが分母に来ます。で、次にbを通ります。そんなわけで分子にbが来ます。sinはその逆と覚えればおっけです。多分、高校に行っていればこうやって習っているはずです・・・
とりあえず公式。
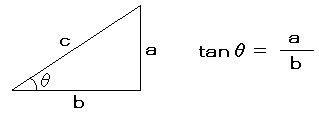
さらに以下のような性質があります。
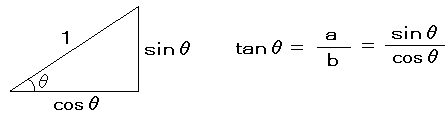
tanで覚えなければいけないのは上の公式と、tan45゜= 1です。なんでそうなるかは下図を参照してください。
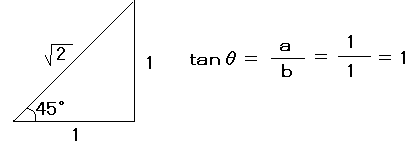
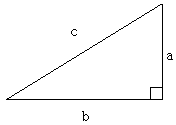
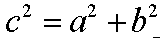 と
と 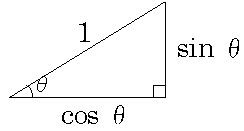 を見比べます。すると以下の公式が成り立つことが分かります。
を見比べます。すると以下の公式が成り立つことが分かります。
重要
![]()
以下の表の空白部分を埋めなさい。
| 0゜ | 30゜ | 45゜ | 60゜ | 90゜ | |
|---|---|---|---|---|---|
| sin | |||||
| cos | 1 | 0 |
答え。超手抜きです。
| 0゜ | 30゜ | 45゜ | 60゜ | 90゜ | |
|---|---|---|---|---|---|
| sin | 0 | 1 | |||
| cos | 1 | 0 |
以下の三角形のaとbの長さをθを使って表しなさい。
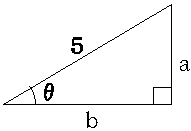
下の図と問題の図を比べると問題の図の三角形の方が5倍大きいです(斜辺が5倍になっています)
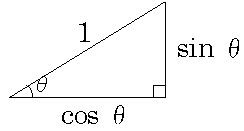
したがって、a = 5sinθ、 b = 5cosθ。
以下の三角形のaの長さをθを使って表しなさい。
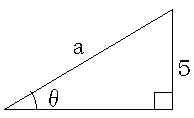
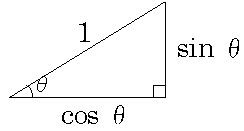
小学生の時にやったように比を使って見ましょう。
a : 5 = 1 : sinθ
a × sinθ = 5 × 1
a × sinθ = 5
a = 5 / sinθ
最初に a : 1 = 5 : sinθ とやっても正解です。
はじめから
a sinθ = 5 なので
a = 5 / sinθ でもOKです。
以下の三角形のdの長さをtanθを使って表しなさい。
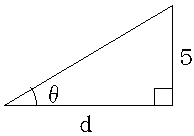

tanθ = 5 / d
d = 5 / tanθ