まず1.の条件です。3cm、4cm、5cmという辺の長さが与えられた時は、どんなに頑張っても下の図のような三角形しか書けません。
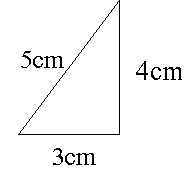
4cmの辺と3cmの辺の間の角は必ず90度になります。ちなみにこれがいわゆる「3:4:5の三角形」というやつです。
三角形を書けと言われたときに、次の3つの条件のうちどれかが与えられれば三角形を書くことが出来ます。
それでは実際に書いてみます。
まず1.の条件です。3cm、4cm、5cmという辺の長さが与えられた時は、どんなに頑張っても下の図のような三角形しか書けません。

4cmの辺と3cmの辺の間の角は必ず90度になります。ちなみにこれがいわゆる「3:4:5の三角形」というやつです。
次に2.の条件です。二つの角が30度、60度でその間の辺の長さが6cm、と与えられたときはどんなに頑張っても下の図のような三角形しか書けません。
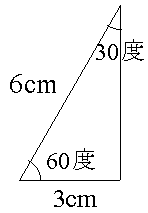
当たり前ですが、残りの角は90度になります。そして、他の辺の長さは3cm、3×31/2になります。(31/2というのは、3のルートのことです。)
ちなみに、これがいわゆる「1:2:ルート3の三角形」というやつです。
最後に3.の条件です。二つの辺の長さがどちらも3cm、その間の角が90度、と与えられた時はどんなに頑張っても下の図のような三角形しか書けません。
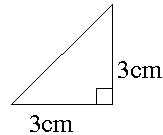
残りの角はどちらも45度になっています。信じられませんでしたら分度器で測ってみてください。斜めになっている辺の長さは3×21/2です。
ちなみに、これがいわゆる「1:1:ルート2の三角形」というやつです。
ここで特に分かって頂きたいのは、三角形ってのは角度と辺の長さで決まるということだけです。
三角形が2つあったとします。その三角形が相似(形が同じだけど大きさが違うってことです)であるためには下記の3つのうち1つを満たしている必要があります。
1.しか重要ではないので1.だけ説明します(ちなみに、高校受験でも1.の条件だけ覚えていれば大丈夫です。私の経験上。難しい高校は別ですけど)。
角度が30度、90度と与えられている三角形が2つあります(辺の長さは違います)。この2つの三角形は相似です。
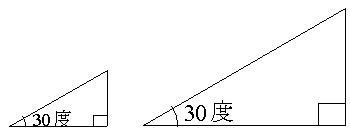
相似な三角形の重要な性質は対応する三つの辺の比が等しいということです。例えば下図をご覧下さい。
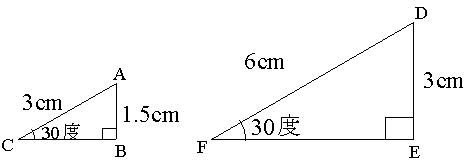
三角形ABC(左の三角形です)において、AB = 1.5cm、AC = 3cm なので、AB:AC = 1:2 です。
三角形DEF(右の三角形です)において、DE = 3cm、DF = 6cmなので、DE:DF = 1:2です。
つまり、角度が30度、90度と与えられている三角形の辺の長さの比は、以下の図のようになります。数字が赤いのは辺の長さと区別するために赤くしてます。
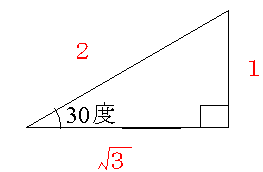
ここで特に分かって頂きたいのは、角度が同じ三角形ってのは対応する三つの辺の比が等しいということです。
上の図でいきなりルート3というのが出ていますが、それは三平方の定理(中学3年生程度)で出てきます。詳細は、次に書きます。
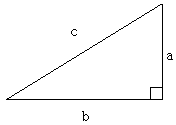
確かピタゴラスの定理とも言ったと思います。下のような三角形があった時、辺の長さには以下の式のような関係があります。証明は当然却下です。周りにいる頭のいい中学3年生にお聞きになって下さい。
![]()
例えば の三角形に三平方の定理をあてはめてみると
の三角形に三平方の定理をあてはめてみると
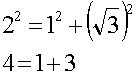
のようになり、確かにいいかなと思えます。
直角三角形において、一番長い辺のことを斜辺といいます。

重要 知らないと話にならないです
以下の4つの三角形を覚えておくだけで、三角形を使う問題の80%(ちょっと控えめ)に対処出来ます。
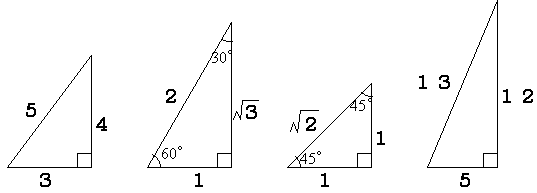
一番左の三角形を3:4:5の三角形といいます。
左から二番目の三角形を1:2:ルート3の三角形といいます。
左から三番目の三角形を1:1:ルート2の三角形といいます。
一番右の三角形を5:12:13の三角形といいます。これは出現頻度が低いです。
三角形を使って数値を計算させる問題の場合、sinθがいくつとか与えられていない限り、かならずこの三角形のどれかに当てはまります。なぜなら、そうじゃないと電卓がないと計算出来ないからです。したがって、三角形が出てきたらまずこのつの三角形を当てはめてください。
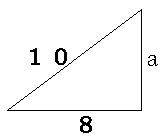
これは3:4:5の三角形なので、aの長さは6になります。
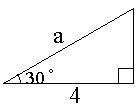
これは1:2:ルート3の三角形です。
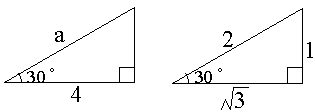
上の図より、aの長さは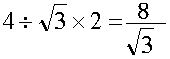 です。
です。
数式打つのが面倒なので、これくらいで許してください。