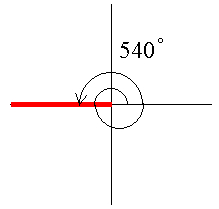
反時計回りに360゜回って、さらに反時計回りに180゜回った角度が540゜です。
ちなみに、-30゜と言ったら、時計回りに30゜回った角度を言います。ラジアンになおすと、-π/6です。
今までは0゜〜90゜の範囲で三角関数を考えました。でも、角度は0゜〜90゜までではなく、360゜とか540゜とかがあります。そこでsin360゜とかcos540゜とかはどのように定義されているのかを考えます。
その前にラジアンというのを定義します。以下は定義です。覚えてください。
2π(rad) = 360゜ radというのはラジアンと読みます。
なんでこんな定義をするかよく知りませんが、多分こうした方が便利なんでしょう。以下に角度とラジアンの対応表を示します。2π(rad) = 360゜を覚えておけば導出できますが慣れればπ/3 = 60゜のようにすぐに頭に浮かびます。私は未だに図を書かないと駄目ですが(^^:
| 度 | 0゜ | 30゜ | 45゜ | 60゜ | 90゜ | 180゜ | 360゜ | 540゜ |
|---|---|---|---|---|---|---|---|---|
| ラジアン | 0 | π/6 | π/4 | π/3 | π/2 | π | 2π | 3π |
ラジアンの単位radは普通は省略します。
540゜が3πというのは納得できますか? 360゜が2πなんですから、540゜は360゜の1.5倍なので2π×1.5=3πです。
例
cos30゜=cos(π/6)
sin60゜=sin(π/3)
cos90゜=cos(π/2)
さて、540゜というのは、そもそもどういう角度なんでしょうか? 540゜を以下の図に示します。

反時計回りに360゜回って、さらに反時計回りに180゜回った角度が540゜です。
ちなみに、-30゜と言ったら、時計回りに30゜回った角度を言います。ラジアンになおすと、-π/6です。
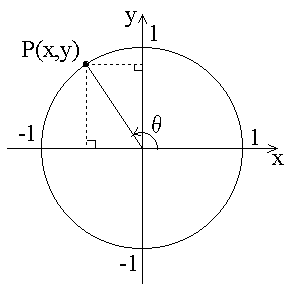
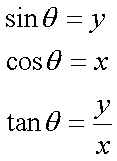
以下に各角度の例を示します。
cos(π/3) = 1/2 なーんてのが、さっと分かるようになるのが、ベストです。
最低限、0,π/6,π/4,π/3,π/2,π,2πラジアンの時のsin,cosの値は言えるようになりましょう。
tanθはめんどいので載せません。自分で、sinθ/cosθを計算してください。
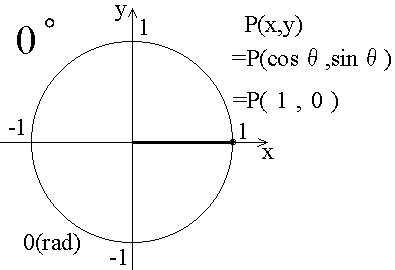
図の説明
左上の数字は角度、左下の数字はラジアンです。
cosθ = 1 , sinθ = 0 ,tanθ = 0/1 = 0です。
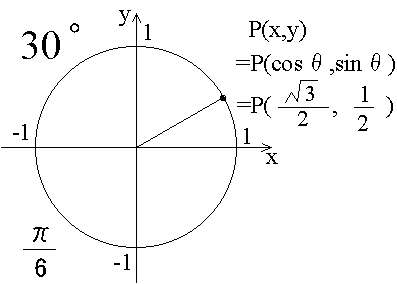
図の説明
cosθ = (ルート3)/2 , sinθ = 1/2 です。以下説明は面倒なので載せません。
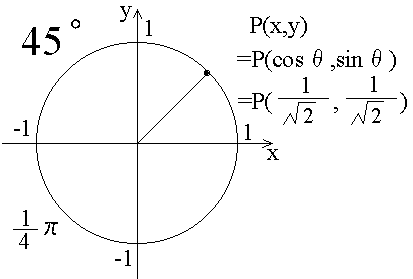
重要 tan(π/4)=1
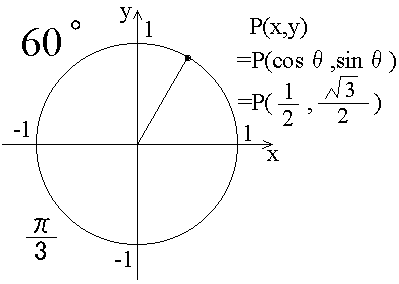
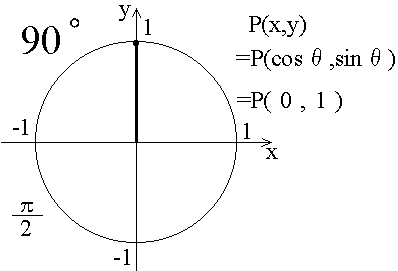
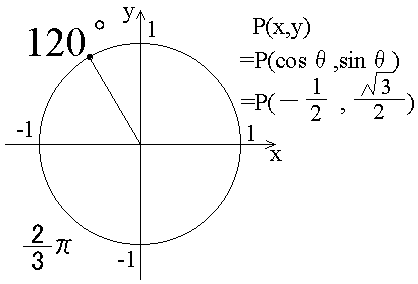
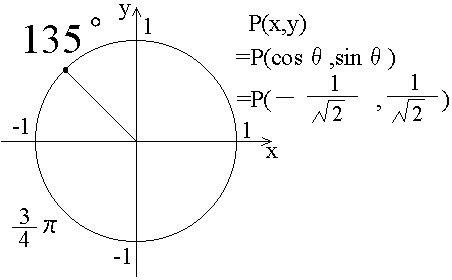
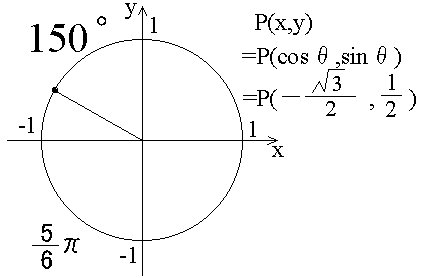
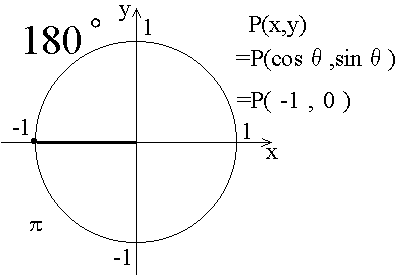
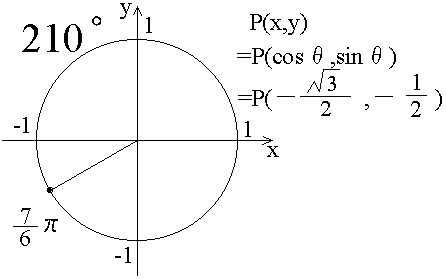
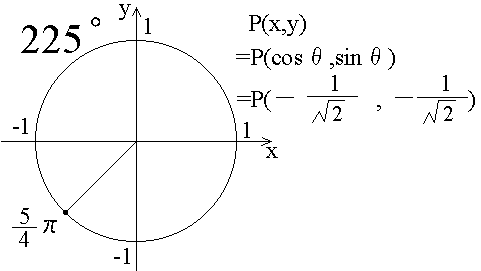
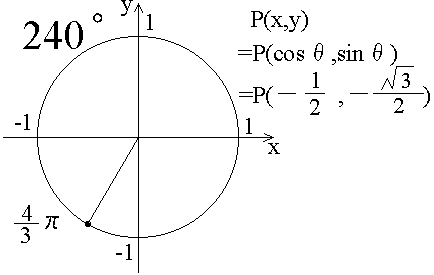
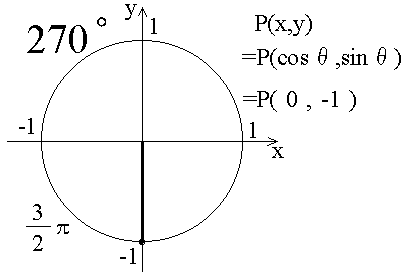
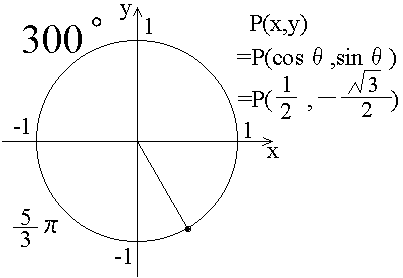
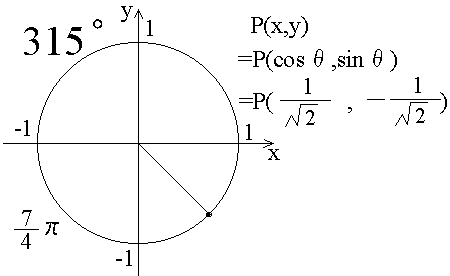
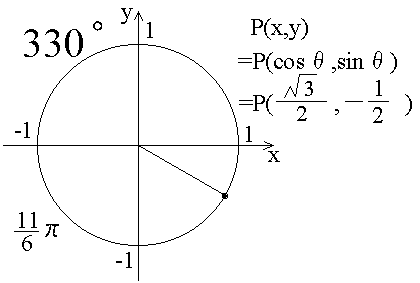
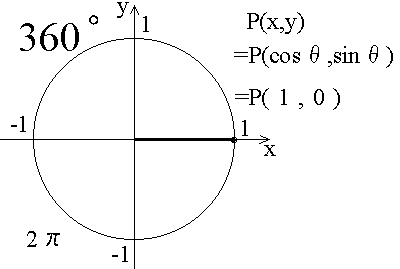
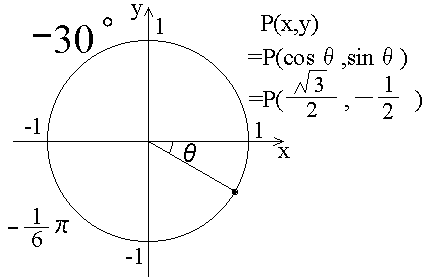
前の節で、θがπの時とか、π/2の時とかのsinθの値、cosθの値の例を書きました。
では、横軸をラジアン、縦軸をsinθとかcosθの値とするとどんなグラフが書けるかというと以下のようになります。
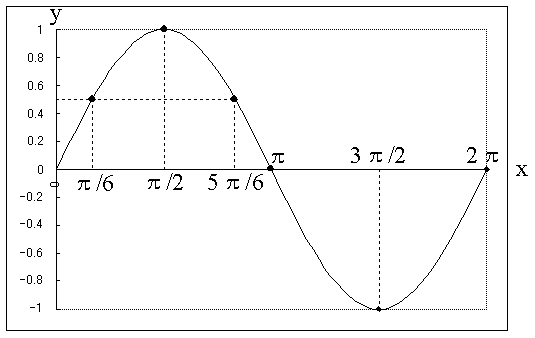
sin(0) = 0 , sin(π/6) = 1/2 , sin(π/2) = 1 のような値をグラフにすると上記のようなグラフになります。2πで一周期です。2πを越えるとまた同じように波の形を描きます。う゛ー、分かりますか?
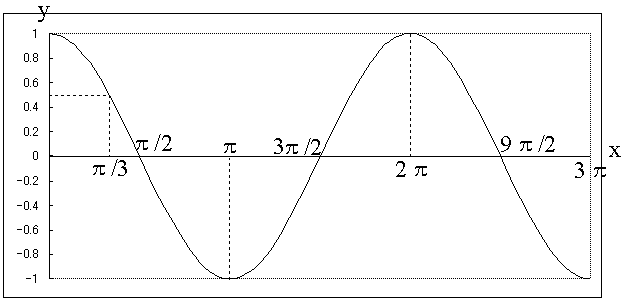
cos(0) = 1 , cos(π/3) = 1/2 , cos(π/2) = 0 のような値をグラフにすると上記のようなグラフになります。やっぱり2πで一周期です。こっちは、3πまでグラフを書いてみました。0〜2πのグラフの形と2π〜4πのグラフの形は同じです。もちろん、4π〜6πのグラフも0〜2πのグラフの形と同じ形になります。
4相PSKなんかでは、電波の位相をずらします。位相というのはなんでしょうか? 簡単に言うとグラフを右や左にずらすことです。以下に位相をずらす例を示します。
位相をπ/3進めると 元の式が y = cosθ ですと、y = cos(θ+π/3) という式になります。位相を進める場合は式の中の符号は+です。位相を遅らせる場合は、式の中の符号は-です。
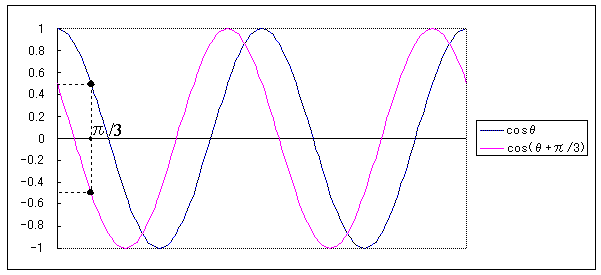
位相を進めるとグラフが左にずれます。
なんで左にずれるのか?を知りたい方は0(rad)とπ/3(rad)の時の値を下に書きますので、見てみてください。それでも納得できませんでしたら、自分でπの時とか2/3πの時とかをグラフ用紙にプロットしてみるとか、Excelでやってみるとかしてください。
cos(0+π/3) = cos(π/3) = 1/2
cos(π/3 + π/3) = cos (2π/3) = -1/2
| ラジアン | 0 | π/3 |
|---|---|---|
| cosθ | 1 | 1/2 |
| cos(θ+π/3) | 1/2 | -1/2 |
sinθの位相をπ/2進めるとcosθになります。
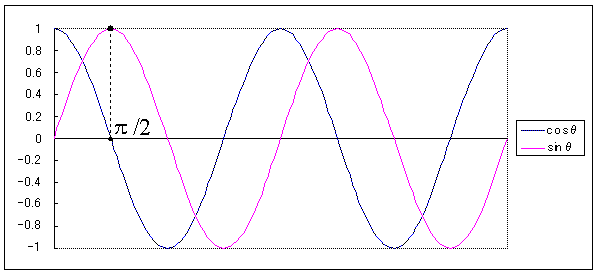
位相をπ/2進めるということは、グラフを左にπ/2だけずらすということです。赤い線(sinθ)を左にπ/2だけずらすと、青い線(cosθ)に重なりますよね。
したがってsin(θ+π/2) = cosθです。
逆にcosθの位相をπ/2だけ遅らせると、sinθになります。π/2遅らせるということは、グラフが右にπ/2だけずれることです。青い線(cosθ)を右にπ/2だけずらすと、赤い線(sinθ)に重なりますよね。
したがってcos(θ-π/2) = sinθです。
cotθ = 1/tanθ