2002擭5寧26擔
堦棨媄
暯惉13擭1寧
A-1丂師偺婰弎偼丄傾儞僥僫偐傜曻幩偝傟傞揹帴奅偲曃攇偺娭學偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪偺惓偟偄慻崌偣傪壓偺斣崋偐傜慖傋丅
(1)丂捈岎偡傞2杮偺慄忬傾儞僥僫偵埵憡偺堎側傞媼揹揹棳傪壛偊偨偲偒丄曻幩偝傟傞揹攇偼丄揹奅偺儀僋僩儖偑帪娫揑媦傃嬻娫揑偵仩A曽岦傪幉偲偟偰夞揮偡傞懭墌曃攇偲側傞丅
(2)丂揹攇偺仩B偵岦偐偭偰屌掕柺撪偺揹奅儀僋僩儖偺夞揮曽岦傪尒偨偲偒丄夞揮曽岦偑帪寁夞傝偺偲偒仩C曃攇丄斀帪寁夞傝偺偲偒仩D曃攇偲偄偆丅
| A | B | C | D |
|---|
| 1 | 揱斃 | 恑峴曽岦偲媡曽岦 | 塃慁 | 嵍慁 |
|---|
| 2 | 揱斃 | 恑峴曽岦 | 塃慁 | 嵍慁 |
|---|
| 3 | 帴奅儀僋僩儖 | 恑峴曽岦偲媡曽岦 | 塃慁 | 嵍慁 |
|---|
| 4 | 帴奅儀僋僩儖 | 恑峴曽岦 | 嵍慁 | 塃慁 |
|---|
| 5 | 帴奅儀僋僩儖 | 恑峴曽岦偲媡曽岦 | 嵍慁 | 塃慁 |
|---|
丂墌曃攇偭偰偳偭偪夞傝偩偭偗丠偲偄偆偺傪偁傫傑傝堄幆偟偰恾傪尒側偄偺偱丄偪傚偭偲偮傜偄偐傕偟傟側偄偱偡丅
丂傑偢姩偱暘偐傝偦偆側偺偼丄仩C偲仩D偱偡丅帪寁夞傝偲尵偭偨傜晛捠塃夞傝丄斀帪寁夞傝偩偭偨傜晛捠嵍夞傝偲峫偊傑偡丅偟偨偑偭偰丄仩C偼塃慁偱仩D偼嵍慁偐側乕偲巚偄傑偡丅
丂仩A丅揹奅儀僋僩儖偲帴奅儀僋僩儖偼屳偄偵捈岎乮偲偄偆傫偩傠偆偐丠乯偺娭學偵偁傝傑偡丅揹奅偑弌棃傞偲帴奅偑弌棃偰丄帴奅偑弌棃傞偲揹奅偑弌棃偰偲偦傫側姶偠偱揹攇偼旘傫偱偄偒傑偡丅栤戣傪撉傓偲d奅儀僋僩儖偑帪娫揑乿偲彂偄偰偁傝傑偡丅偠傖偁乽帴奅儀僋僩儖傕帪娫揑乿偲峫偊傞偺偑晛捠偱偡丅偮偄偱偵晛捠偵峫偊偰丄乽帴奅儀僋僩儖曽岦偑幉乿偲乽揱斃曽岦偑幉乿偱偼屻幰偺曽偑偟偭偔傝偒傑偡丅偟偨偑偭偰仩A偼揱斃偱偡丅
丂偝偰丄仩B丅姩偱偡丅側傫偲側偔恑峴曽岦偵岦偐偭偰夞揮曽岦傪尒傞偲偄偆偺偑偟偭偔傝偒偦偆偱偡丅摎偊偼乽恑峴曽岦乿偱偡丅
丂曃攇偵娭偟偰偼暯栰戱堦偺儂乕儉儁乕僕偺揹帴奅棟榑偺曃攇傪尒傞偲偄偄偐側乕偲巚偄傑偡丅
A-2丂師偺婰弎偼丄恾乮暯柺恾乯偵帵偡傛偆偵丄2屄偺悅捈敿攇挿僟僀億乕儖傾儞僥僫傪娫妘l[m]偱摨堦悈暯柺忋偵暯峴偵暲傋偨偲偒偺悈暯柺撪偺巜岦惈傪媮傔傞夁掱偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪偺惓偟偄慻崌偣傪壓偺斣崋偐傜慖傋丅偨偩偟丄仩撪偺摨偠婰崋偼摨偠帤嬪傪帵偡丅傑偨傾儞僥僫揹棳偺妏廃攇悢傪冎[rad/s]丄攇挿傪兩[m]丄l<<兩偲偟丄椉傾儞僥僫偺揹棳偺怳暆偲埵憡偼摍偟偔丄戝抧側偳偺塭嬁偼側偄傕偺偲偡傞丅
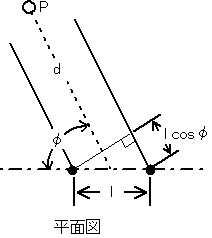
(1)丂椉傾儞僥僫偐傜偺暯嬒妏搙冇[rad]偺曽岦偱丄暯嬒嫍棧d[m]偺廫暘墦曽偺揰P傜偍偗傞崌惉偺揹奅嫮搙E偼丄椉傾儞僥僫偐傜偺揹奅嫮搙偑摍偟偄偲偟偰師幃偺傛偆偵昞偝傟傞丅偨偩偟丄學悢K偼丄傾儞僥僫揹棳偲嫍棧偺娭悢偱偁傞丅傑偨丄(ej兝+e-兝)/2=cos兝偺娭學偑偁傞丅
丂丂E佮K[ej(冎t-2兾d/兩)+ej(冎t-2兾(d+lcos冇)/兩)]
丂丂丂=2Kcos(仩A)ej(冎t-2兾(d+lcos冇)/兩) [V/m]丂丒丒丒嘆
(2)丂幃嘆傛傝丄椉傾儞僥僫偺拞怱傪娷傓悈暯柺偺巜岦惈學悢D(冇)偼丄師幃偱昞偝傟傞丅
丂丂D(冇)=cos(仩A)丂丒丒丒嘇
(3)丂幃嘇偐傜丄l=兩/2偲偡傟偽丄冇偑0媦傃兾偱D(冇)=仩B丄傑偨丄冇偑兾/2媦傃3兾/2偱D(兤)=仩C偲側傝丄悈暯柺偱偼仩D偺巜岦惈偲側傞丅
| A | B | C | D |
|---|
| 1 | (兾lsin冇)/兩 | 0 | 1 | 扨堦巜岦惈 |
|---|
| 2 | (兾lcos冇)/兩 | 1 | 1 | 慡曽岦惈 |
|---|
| 3 | (兾lcos冇)/兩 | 0 | 1 | 8帤宍 |
|---|
| 4 | (兾lcos冇)/兩 | 0 | 1 | 扨堦巜岦惈 |
|---|
| 5 | (兾lsin冇)/兩 | 1 | 0 | 8帤宍 |
|---|
丂側傫偐擄偟偄幃偑弌偰偒傑偡偑丄幃偵榝傢偝傟側偄傛偆偵偟傑偟傚偆丅
丂傑偢仩D偱偡丅崱夞弌偰偒偰偄傞傾儞僥僫偼敿攇挿僟僀億乕儖傾儞僥僫偑2偮偱偡丅悅捈敿攇挿僟僀億乕儖傾儞僥僫偺悈暯柺偺巜岦惈偼柍巜岦惈偱偡丅偙傟傪2偮慻崌傢偣偨偲偒乽扨堦巜岦惈乿偵側傞偲偼峫偊傜傟傑偣傫丅敧栘傾儞僥僫偺傛偆偵悈暯敿攇挿僟僀億乕儖傾儞僥僫傪2偮暲傋偨帪偺悈暯柺偺巜岦惈側傜丄巜岦偼偡傞偳偔側傝傑偡偑丅傑偨丄悅捈敿攇挿僟僀億乕儖傾儞僥僫1杮偱偡偲柍巜岦惈丄偮傑傝慡曽岦偵揹攇偑旘傃傑偡偗偳丄2杮慻崌傢偣偰巜岦惈偑摨偠偲偄偆偺傕峫偊偢傜偄偱偡丅偟偨偑偭偰仩D偼8帤宍偱偡丅
丂師偵仩A丅傑偠傔偵夝偄偰傕偄偄傫偱偡偑丄栤戣暥拞偵乽(ej兝+e-兝)/2=cos兝偺娭學偑偁傞乿偲偁傝傑偡丅偟偨偑偭偰乽[ej(冎t-2兾d/兩)+ej(冎t-2兾(d+lcos冇)/兩)]乿傪側傫偐偄偠傞偲cos偵側傞傫偩傠偆偲峫偊傜傟傑偡丅偟偨偑偭偰仩A偼(兾lcos冇)/兩傪慖傃傑偡丅嶰妏娭悢偺崌惉偐側傫偐巊偭偰sin偵側傞偐傕偟傟側偄偲巚偆曽傕偄傞偐傕偟傟傑偣傫偑丄棨媄偺帋尡偱偼崌惉娭悢傪巊偆応崌偼昁偢偦偺岞幃偑帵偝傟傑偡丅偮偄偱偵丄棨媄偺帋尡偱偼sin偲cos傪慖傇側傜偽cos偺曽偑暘偑偄偄偱偡丅偟偨偑偭偰傛偔暘偐傜側偐偭偨傜cos傪慖傫偱偔偩偝偄丅
丂偁偲偼丄仩B偲仩C偼(兾lcos冇)/兩偵抣傪戙擖偡傞偩偗偱偡丅
丂摎偊偼3偱偡丅
丂偪側傒偵仩D偺巜岦惈偑偳乕偟偰傕慖傋側偐偭偨応崌偼丄仩B偲仩C傪愭偵夝偒傑偡丅
丂傑偢仩A偺夝摎偑(兾lcos冇)/兩偩偭偨偲偟偨傜偳偆側傞偐偲寁嶼偟偰尒傞偲仩B偑0丄仩C偼1偲側傝傑偡丅摨偠偔丄仩A偺夝摎偑(兾lsin冇)/兩偩偭偨偲偟偨偲偒偼仩B偼1丄仩C偼0偲側傝傑偡丅偡傞偲丄慖傋傞夝摎偺慖戰巿偼3丄4丄5偺偳傟偐偵側傝傑偡丅屻偼塣偱偡偹丅傫偱傕棨媄傪庴偗傞傫偱偟偨傜乽悅捈敿攇挿僟僀億乕儖傪暲傋偰抲偄偨偲偒偼丄偳乕峫偊偰傕悈暯柺偺巜岦惈偼扨堦偵偼側傜傫乿偔傜偄偼僺儞偲偒偰梸偟偄偱偡丅
A-3丂廃攇悢偑100[MHz]丄揹奅嫮搙偑2[mV/m]偺揹攇傪慺巕偺懢偝偑摍偟偄2慄幃愜傝曉偟敿攇挿僟僀億乕儖傾儞僥僫偱庴怣偟偨偲偒偺傾儞僥僫偺桿婲揹埑(庴怣奐曻揹埑)Vo[V]偲庴怣婡擖椡揹埑Vr[V]偺慻崌偣偲偟偰丄惓偟偄傕偺傪壓偺斣崋偐傜慖傋丅偨偩偟丄傾儞僥僫夞楬偲庴怣婡偺擖椡夞楬偼惍崌偟偰偍傝丄傾儞僥僫偺嵟戝姶搙偺曽岦偼摓棃揹攇偺曽岦偲堦抳偟偰偄傞傕偺偲偡傞丅
| Vo | Vr |
|---|
| 1 | 3.8[mV] | 3.8[mV] |
|---|
| 2 | 3.8[mV] | 1.9[mV] |
|---|
| 3 | 1.9[mV] | 1.9[mV] |
|---|
| 4 | 1.9[mV] | 0.9[mV] |
|---|
| 5 | 0.9[mV] | 0.9[mV] |
|---|
丂敿攇挿僟僀億乕儖傾儞僥僫偺幚岠崅乮廳梫乯偲傾儞僥僫偵桿婲偡傞揹埑乮廳梫乯偲愜傝曉偟敿攇挿僟僀億乕儖傾儞僥僫偺宍偑暘偐偭偰偄傟偽側傫偲偐側傞栤戣偱偟傚偆丅
敿攇挿僟僀億乕儖傾儞僥僫偺幚岠挿

丂le[m]乮傾儞僥僫偺幚岠挿乯丂兩[m]乮攇挿乯
傾儞僥僫偵桿婲偡傞揹埑

丂倁[V]乮揹埑乯丂俤[V/m]乮揹奅乯丂le[m]乮傾儞僥僫偺幚岠挿乯
偱偡丅
愜傝曉偟僟僀億乕儖傾儞僥僫

丂傑偢傾儞僥僫偵桿婲偡傞揹埑傪媮傔傑偡丅
丂偲傝偁偊偢敿攇挿僟僀億乕儖傾儞僥僫偩偭偨傜偳偺偔傜偄偐側偲寁嶼偟偰傒傑偡丅
丂Vo=Ele=E兩/兾
丂攇挿兩[m]偼廃攇悢偑100[MHz]側偺偱丄300/100=3[m]
丂偟偨偑偭偰丄Vo[mV]=2[mV/m]亊3[m]亐兾=1.91[mV]丅愜傝曉偟僟僀億乕儖傾儞僥僫傪尒傞偲傾儞僥僫偺慺巕偑2杮偁傝傑偡偺偱乽庴怣揹埑偼2攞偵側傞傫偠傖側偄偐側乕乿偲巚偄傑偡丅1.91[mV]傪2攞偟偰3.8[mV]偱偡丅
丂摎偊偼1偐2偺偳偪傜偐偱偡丅偁偲偼塣偱偡丅塣偱偡偑丄慺杙偵峫偊偰乽傾儞僥僫偺揹椡偑偦偺傑傑庴怣婡偵峴偔傢偗偑側偄乿偲巚偆偺偱丄乽壗偐棟桼偑偁偭偰敿暘偵側傞傫偠傖側偄偐側乕乿偲巚偄傑偡丅偟偨偑偭偰摎偊偼2偱偡丅壓偵敿暘偵側傞揔摉側棟桼傪丅
庴怣婡偵桿婲偡傞揹埑
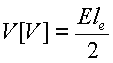
丂倁[V]乮揹埑乯丂俤[V/m]乮揹奅乯丂le[m]乮傾儞僥僫偺幚岠挿乯
丂2偱妱傞棟桼偼嶲峫彂偱乽桳岠揹椡乿偁偨傝傪挷傋傞偲嵹偭偰傞偱偟傚偆丅揔摉偵愢柧偟傑偡偲丄傾儞僥僫偺桿婲揹埑傪V[V]丄傾儞僥僫偺僀儞僺乕僟儞僗偑R1丄庴怣婡偺僀儞僺乕僟儞僗偑R2偲偡傞偲丄傾儞僥僫偲庴怣婡偼捈楍偵宷偑偭偰偄傞偺偱丄R1偵V/2[V]偺揹埑偑偐偐偭偰丄R2偵V/2[V]偺揹埑偑偐偐傞偐傜偱偡丅
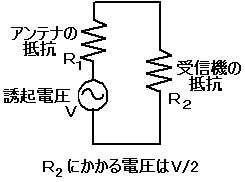
丂偪側傒偵丄偙傟偼夞楬偑惍崌偟偰傞帪偱偡丅
A-4丂旝彫揹婥僟僀億乕儖傾儞僥僫偺幚岠柺愊傪昞偡幃偲偟偰丄惓偟偄傕偺傪壓偺斣崋偐傜慖傋丅偨偩偟丄旝彫揹婥僟僀億乕儖偺挿偝傪l[m]媦傃攇挿傪兩[m]偲偡傟偽曻幩掞峈Rr偼丄師幃偱梌偊傜傟傞丅
丂Rr=80兾2l2/兩2[兌]
1丂兩2/兾[m2]
2丂兩2/2兾[m2]
3丂兩2/4兾[m2]
4丂3兩2/4兾[m2]
5丂3兩2/8兾[m2]
丂偙偺栤戣偼傛偔弌傑偡丅偩偐傜妎偊偰偔偩偝偄丅寁嶼偡傞傛傝妎偊偨傎偆偑憗偄偱偡丅摎偊偼5偱偡丅
旝彫僟僀億乕儖傾儞僥僫偺幚岠柺愊
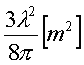
兩[m](攇挿)
A-5丂師偺婰弎偼丄傾儞僥僫偺摿惈偵偮偄偰弎傋偨傕偺偱偁傞丅偙偺偆偪岆偭偰偄傞傕偺傪壓偺斣崋偐傜慖傋丅
1丂奐岥柺傾儞僥僫偺愨懳棙摼偼丄奐岥柺愊偵斾椺偡傞丅
2丂摍曽惈傾儞僥僫偺幚岠柺愊偼丄攇挿傪兩偲偡傟偽丄兩2/4兾偱偁傞丅
3丂奐岥柺傾儞僥僫偺奐岥岠棪偼丄奐岥柺愊傪S丄幚岠柺愊傪Se偲偡傟偽丄Se/S偱偁傞丅
4丂慄忬傾儞僥僫偺幚岠柺愊偼丄慄偺捈宎偲慡挿偲偺愊偱偁傞丅
5丂奐岥柺傾儞僥僫偺愨懳棙摼傪G媦傃幚岠柺愊傪Se丄摍曽惈傾儞僥僫偺幚岠柺愊傪S0偲偡傟偽丄G=Se/S0偱偁傞丅
丂壗傕抦幆偑側偄偲塣傑偐偣偺栤戣偱偡丅偑丄傛偔傛偔峫偊傞偲暘偐傝傑偡丅
丂A-4偺栤戣偱旝彫僟僀億乕儖傾儞僥僫偺幚岠柺愊偑暘偐偭偰偄傑偡丅偦偟偰偙偺栤戣偺4斣傪撉傒傑偡丅旝彫僟僀億乕儖傾儞僥僫偺幚岠柺愊偼慄偺捈宎偲慡挿偲偺愊偵側偭偰傑偣傫丅偟偨偑偭偰丄摎偊偼4偱偡丅偪側傒偵丄幚岠柺愊娭學偺幃偼傛偔巊偄傑偡偺偱埫婰偟偰偍偒傑偟傚偆丅
傾儞僥僫偺幚岠柺愊側偳側偳乮廳梫乯

丂俙e[m2]乮傾儞僥僫偺幚岠柺愊乯丂俙 [m2]乮傾儞僥僫偺柺愊乯丂兩 [m]乮攇挿乯丂俧 [扨埵側偟]乮棙摼乯丂兣[扨埵側偟]乮奐岥岠棪乯
丂尭悐掕悢兛丒丒丒弌傞偲巚偭偰傑偣傫偱偟偨丅巹偼帋尡帪偵偼埫婰偟偰偄偨偺偱偡偑丄偡偭偐傝朰傟偰偄傑偟偨丅
丂偁傫傑傝弌側偄偐傕偟傟傑偣傫偑丄梋桾偑偁傟偽摿惈僀儞僺乕僟儞僗丄揱斃掕悢兞丄尭悐掕悢兛丄埵憡掕悢兝偺幃偲偦偺嬤帡幃傪姰慡偵偱偼側偔偰偄偄偺偱僀儊乕僕偲偟偰妎偊偰偍偔偲偄偄偐傕偟傟傑偣傫丅
丂偙偺栤戣偺巜恓偲偟偰偼丄幃嘇偺()偺拞偺暘曣偵2偑擖偭偰偄傞偺偱夝摎偵傕2偑擖偭偰偄傞偲峫偊傞偺偑僗僕偱偡丅偟偨偑偭偰丄慖戰巿偺3偲4偼媝壓偱偡丅摎偊偼1偐2偐5偱偡丅偁偲偼塣偱偡偹丅
丂摎偊偼1偱偡丅
A-7丂師偺婰弎偼丄摫攇娗偺揱憲儌乕僪偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪偺惓偟偄慻崌偣傪壓偺斣崋偐傜慖傋丅偨偩偟仩撪偺摨偠婰崋偼丄摨偠帤嬪傪帵偡丅
(1)丂曽宍摫攇娗偺婎杮儌乕僪偼丄仩A儌乕僪偱偁傝丄堦斒偵偙偺儌乕僪偑梡偄傜傟偰偄傞丅曽宍摫攇娗偺悰幉偵捈妏側抐柺撪懁偺挿曈偺挿偝傪a[m]丄抁曈偺挿偝傪b[m]偲偡傟偽丄a=仩B偵慖傃丄a<兩<2a偺攇挿偱梡偄傟偽丄仩A儌乕僪偺傒傪揱憲偡傞偙偲偑偱偒傞丅偨偩偟丄兩[m]傪攇挿偲偡傞丅
(2)丂墌宍摫攇娗偺TE01儌乕僪偼丄廃攇悢偑仩C側傞傎偳尭悐掕悢偑彫偝偔側傞惈幙偑偁傞丅
| A | B | C |
|---|
| 1 | TE10 | 3b/2 | 掅偔 |
|---|
| 2 | TM10 | 3b/2 | 掅偔 |
|---|
| 3 | TM10 | 3b/2 | 崅偔 |
|---|
| 4 | TM10 | 2b | 崅偔 |
|---|
| 5 | TE10 | 2b | 崅偔 |
|---|
丂摫攇娗偺婎杮傪抦偭偰偄傟偽2戰偺栤戣偱偡丅
丂摫攇娗偺婎杮儌乕僪偲尵偭偨傜丄TE10偱偡丅
丂偙傟偱1偐5偺擇戰偱偡丅偁偲偼塣偱偡丅
丂偑丄墌宍摫攇娗偺TE01儌乕僪偼廃攇悢偑崅偔側傞偲尭悐掕悢偑彫偝偔側傞偲偄偆惈幙偑偁傞偺偼妎偊偰偍偄偰偄偄偐傕偟傟側偄偱偡丅偳偭偐偱堦夞弌偨婰壇偑偁傝傑偡丅
丂摎偊偼5偱偡丅
摫攇娗偺幷抐攇挿
丂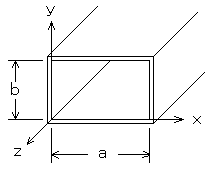
丂幷抐攇挿亖 2a[m]
丂埵憡懍搙偲孮懍搙偱偼孮懍搙偺曽偑抶偄
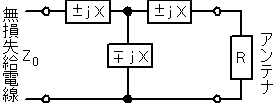 A-8丂恾偵帵偡傛偆偵丄摿惈僀儞僺乕僟儞僗Z0偑50[兌]偺柍懝幐媼揹慄偲擖椡掞峈R偑100[兌]偺傾儞僥僫傪懳徧宍廤拞掕悢夞楬傪梡偄偰愙懕偟偨偲偒丄偙偺夞楬偑惍崌偡傞偨傔偺夞楬掕悢X偲偟偰丄嵟傕嬤偄傕偺傪壓偺斣崋偐傜慖傋丅
A-8丂恾偵帵偡傛偆偵丄摿惈僀儞僺乕僟儞僗Z0偑50[兌]偺柍懝幐媼揹慄偲擖椡掞峈R偑100[兌]偺傾儞僥僫傪懳徧宍廤拞掕悢夞楬傪梡偄偰愙懕偟偨偲偒丄偙偺夞楬偑惍崌偡傞偨傔偺夞楬掕悢X偲偟偰丄嵟傕嬤偄傕偺傪壓偺斣崋偐傜慖傋丅
1丂56[兌]
2丂63[兌]
3丂71[兌]
4丂75[兌]
5丂112[兌]
丂儃乕僫僗栤戣偱偡丅僀儞僺乕僟儞僗偑2偮梌偊傜傟偰惍崌偺栤戣偱偟偨傜丄偲傝偁偊偢妡偗嶼偟偰儖乕僩偱偡丅
丂偙偺栤戣偼(50亊100)1/2偱71[兌]丅摎偊偼3偱偡丅
1/4攇挿惍崌夞楬
 偺偲偒丄
偺偲偒丄
丂Z0[兌]乮摿惈僀儞僺乕僟儞僗乯丂Zq[兌]乮1/4攇挿惍崌夞楬偺摿惈僀儞僺乕僟儞僗乯丂R[兌]乮晧壸掞峈乯
丂崱夞偼1/4攇挿惍崌夞楬偠傖側偔偰丄懳徧宍廤拞掕悢惍崌夞楬偱偡偑丄摨偠傛偆側姶偠偱偡丅偲傝偁偊偢丄妡偗嶼偟偰儖乕僩偱偡丅偲偒偳偒Z0傪媮傔傠偲偄偆栤戣偑偁傝傑偡偺偱婥傪偮偗傑偟傚偆丅偦偺応崌偼丄Zq傪2忔偟偰妱傝嶼偱偡丅
A-9丂師偺婰弎偼丄媼揹夞楬偺梡偄傜傟傞摨幉慄楬偵偮偄偰弎傋偨傕偺偱偁傞丅偙偺偆偪岆偭偰偄傞傕偺傪壓偺斣崋偐傜慖傋丅
1丂庡偵揱斃曽岦偵揹帴奅惉暘偺側偄TEM儌乕僪偑梡偄傜傟傞丅
2丂捠忢丄崅師儌乕僪偑敪惗偡傞崅偄廃攇悢偱偼梡偄傜傟傑偡丅
3丂斾桿揹棪兠s偺桿揹懱偑廩偰傫偝傟偰偄傞応崌偺摿惈僀儞僺乕僟儞僗偼丄斾桿揹棪偑1偺応崌偺1/兠s偲側傞丅
4丂撪晹摫懱丄奜晹摫懱偲傕偵捈宎偺懢偄摵娗傪梡偄偨摵娗摨幉慄楬偼丄戝揹椡偺揱憲偵梡偄傜傟傞丅
5丂傾儖儈僔乕僗摨幉働乕僽儖偼丄敿壜偲偆惈偱偁傝丄撪晹摫懱偲奜晹摫懱偺娫偵憓擖偝傟傞愨墢暔偑摵娗摨幉慄楬偵斾傋偰懡偄偨傔丄尭悐掕悢偑彮偟戝偒偄丅
丂儃乕僫僗栤戣偱偡丅
摨幉慄楬偺摿惈僀儞僺乕僟儞僗


丂Z0[兌]乮摿惈僀儞僺乕僟儞僗乯丂D[m]乮奜晹摫懱偺撪宎乯丂d[m]乮撪晹摫懱偺奜宎乯丂兠r(斾桿揹棪)
丂忋偺帠幚偼抦偭偰偄傞傋偒傕偺側偺偱丄埫婰偟偰偔偩偝偄丅偙偺幃傛傝摿惈僀儞僺乕僟儞僗偼1/(兠s)1/2偵側傝傑偡偺偱丄3偼娫堘偭偰傑偡丅
丂偝偰丄偙偆偄偆乽岆偭偨傕偺傪扵偡栤戣乿偺応崌偼乽惓偟偄慖戰巿偺暥復傪側傞傋偔埫婰偡傞乿傛偆偵偟偰偔偩偝偄丅壗偑岆偭偰偄傞偐傛傝傕丄惓偟偄慖戰巿傪妎偊傞曽偑桳塿偱偡丅
丂偪側傒偵廳梫側偺偼慖戰巿1偺乽摨幉慄楬偼TEM乿丄2偺乽摨幉慄楬偼崅偄廃攇悢偼懯栚乿偺2偮偱偡丅4偲5偼偁傫傑傝妎偊側偔偰偄偄婥偑偟傑偡丅
A-10丂師偺婰弎偼丄恾偵帵偡僗儘僢僩傾儗乕傾儞僥僫乮僗儕僢僩傾儗乕傾儞僥僫乯偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪偺惓偟偄慻崌偣傪壓偺斣崋偐傜慖傋丅
(1)丂曽宍摫攇娗偺懁柺偵堦掕偺孹幬妏偱孹幬曽岦偑媡岦偒偵側傞傛偆偵偟偰丄僗儘僢僩拞怱娫偺娫妘偑娗撪攇挿偺仩A掱搙偱僗儘僢僩傪愗偭偨傕偺偱偁傞丅
(2)丂摫攇娗撪傪揹帴攇偑婎杮儌乕僪偱揱斃偟偰偄傞偲偒丄曻幩偝傟傞揹攇偺曃攇偼丄僗儘僢僩偺孹幬曽岦偑岎屳偵媡岦偒偵側偭偰偄傞偨傔丄娗撪偺揹奅曽岦偲仩B側曽岦偲側傞丅
(3)丂僗儘僢僩偺悢傪懡偔偡傞偲丄巜岦惈偼丄摫攇娗偺幉偵捈妏側柺撪偺價乕儉暆偑仩僼傽儞價乕儉偲側傞丅
| A | B | C |
|---|
| 1 | 1/2攇挿 | 捈妏 | 峀偄 |
|---|
| 2 | 1/2攇挿 | 暯峴 | 嫹偄 |
|---|
| 3 | 1攇挿 | 捈妏 | 嫹偄 |
|---|
| 4 | 1攇挿 | 暯峴 | 峀偄 |
|---|
| 5 | 1攇挿 | 捈妏 | 峀偄 |
|---|
丂僗儘僢僩傾儗乕傾儞僥僫偺栤戣偼傛偔弌偰偔傞偺偱偡偑丄偪傚偭偲栄怓偺堘偆栤戣偱偡丅恾傪彂偔偺偑柺搢側傫偱彂偒傑偣傫丅
丂傑偢仩A丅僗儘僢僩傾儗乕傾儞僥僫偑弌偰偔傞応崌偵偼昁偢弌戣偝傟傞偺偱妎偊偰偔偩偝偄丅乽娗撪攇挿偺1/2乿偱偡丅偙傟偼抦偭偰偍偐側偄偲懯栚偱偡丅偡傞偲慖戰巿偼1偐2偵側傝傑偡丅屻偼塣偱偡丅
丂摎偊偼1偩偦偆偱偡丅
丂僗儘僢僩傾儗乕傾儞僥僫偼慏敃偱巊傢傟傞偦偆偱偡丅偦偺棟桼傪埲壓偵帵偟傑偡丅
丂傑偢僼傽儞價乕儉偵偮偄偰丒丒丒抦傝偨偐偭偨傫偱偡偗偳丄僼傽儞價乕儉儗乕僟乕偟偐偍庤寉偵尒偮偐傜側偐偭偨傫偱丄僼傽儞價乕儉儗乕僟乕偵偮偄偰丅僼傽儞價乕儉儗乕僟偲偼丆憲怣偡傞揹攇偺抐柺偑儁儞僔儖價乕儉儗乕僟偺傛偆偵墌宍偱側偔丆揹攇偑愵偺傛偆偵堦曽岦偵峀偑偭偰偄傞傕偺傪偄偆丅慏敃梡偺僼傽儞價乕儉儗乕僟偼丆堦斒揑偵悅捈曽岦偵揹攇偑峀偑偭偰偄傞
偦偆偱偡丅
丂幚嵺偺傾儞僥僫偺僗儁僢僋傪尒偰傒傞偲丄悈暯價乕儉暆1.2搙丄悅捈價乕儉暆25搙丄偵側偭偰偄傑偡丅偙傟傪尦偵偳傫側晽偵揹攇偑旘傇偺偐側乕偲峫偊傞偲懡暘埲壓偺傛偆偵側傞偐偲丅
丂
丂愒偄姶偠偱揹攇偑旘傫偱偄偭偰偄傞偐偲丒丒丒
丂慏敃偱偼慏偑攇偵傛偭偰廲偵備傟傞偺偱丄偙偆偄偆巜岦惈傪帩偭偰偄傞偲攇偺備傟傪傾儞僥僫偺曽偱媧廂偱偒傞偺偱慏偱傛偔棙梡偝傟傞偲偺偙偲偱偡丅
A-11丂師偺婰弎偼丄拞攇曻憲梡偺悅捈愙抧傾儞僥僫媦傃抁攇曻憲梡偺價乕儉傾儞僥僫乮僇乕僥儞傾儞僥僫乯偵偮偄偰弎傋偨傕偺偱偁傞丅偙偺偆偪岆偭偰偄傞傕偺傪壓偺斣崋偐傜慖傋丅
1丂僼僃乕僕儞僌杊巭傾儞僥僫偼丄僒乕價僗僄儕傾偑100僉儘儊乕僩儖埲忋偺戝揹椡曻憲偵梡偄偨偲偒桳岠偱偁傞丅
2丂悅捈愙抧傾儞僥僫偼丄巜岦惈傪帩偨偣傞偨傔偵柍媼揹慺巕傪庡傾儞僥僫偵暪愝偡傞偙偲偑偁傞丅
3丂悅捈愙抧傾儞僥僫偼丄捀姤傪愝偗傞偲傾儞僥僫偺崅偝傪掅偔偡傞偙偲偑弌棃傞丅
4丂價乕儉傾儞僥僫偼丄揹棧憌偺曄壔偵傛偭偰惗偢傞媧廂惈僼僃乕僕儞僌傪彫偝偔偡傞偙偲偑偱偒傞丅
5丂價乕儉傾儞僥僫偼丄巜岦惈崌惉偵傛傝塻偄巜岦惈傪摼傞傾儗乕傾儞僥僫偱偡丅
丂梡岅傪傛偔抦傜側偔偰傕乽側傫偲側偔偙偆偐側乿偲峫偊傞偲摉偨傞偱偟傚偆丅巹偼摉偨傝傑偟偨丅
丂傑偢1丅傫乕丄偦偆偄偆傕傫側偺偐側偁偲巚偭偰曐棷丅
丂2斣丅敧栘傾儞僥僫偲偄偆偺偼悈暯傾儞僥僫偱偡偑丄偙偄偮偼巜岦惈傪帩偨偣傞偨傔柍媼揹慺巕傪暪愝偟偰偄傑偡丅悅捈傾儞僥僫偱傕摨偠偙偲偑弌棃傞偩傠偆側乕偲巚偆偺偱懡暘惓偟偄偲巚偄傑偡偑丄傗偭傁傝曐棷丅
丂3斣丅傛偔傢偐傫側偄偱偡丅偗偳丄捀姤傪偮偗傞偲傾儞僥僫偺崅偝偑掅偔側傞偲偄偆偺偼丄側傫偐傕偭偲傕傜偟偄偱偡丅曐棷丅
丂4斣丅媧廂惈僼僃乕僕儞僌偭偰側傫偩偭偗丠偲峫偊傑偡丅偱丄揹棧憌偑揹攇傪媧廂偡傞妱崌偑曄壔偟偰揹攇偑嫮偔側偭偨傝庛偔側偭偨傝偡傞傫偐側偁偲峫偊傑偡丅偦傫側揹攇偵丄巜岦惈偑偡傞偳偄偩偗偺價乕儉傾儞僥僫偑僼僃乕僕儞僌傪挷愡偱偒傞偲偼巚偊傑偣傫丅娫堘偭偰傞偺偼丄偙傟偭傐偄偲巚偄傑偡丅
丂5斣丅偙傟偼柍慄壆偝傫偺忢幆偲偟偰抦偭偰偍偄偰偔偩偝偄丅價乕儉傾儞僥僫偼價乕儉傒偨偄偵揹攇偑旘傇偺偱價乕儉傾儞僥僫偱偡乮偲巹偼巚偭偰傑偡丅儂儞僩偐偳偆偐抦傝傑偣傫乯丅
丂偙偙偱丄1乣4傪専摙偟偰傗偭傁傝4斣偑堦斣夦偟偄偺偱4斣偲偟傑偟偨丅摎偊偼4斣偱偡丅
丂乽悅捈愙抧傾儞僥僫偼丄巜岦惈傪帩偨偣傞偨傔偵柍媼揹慺巕傪庡傾儞僥僫偵暪愝偡傞偙偲偑偁傞乿椺傪丅偙傟丄悅捈愙抧傾儞僥僫偠傖側偄偗偳丄傑偁丄偍傫側偠傛偆側傕傫偱偟傚偆丅
丂
丂偪側傒偵丄偙傟偼億働儀儖偺傾儞僥僫偱偡丅
A-12丂師偺婰弎偼丄奐岥柺傾儞僥僫偺僒僀僪儘乕僽偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪偺惓偟偄慻傒崌傢偣傪壓偺斣崋偐傜慖傋丅
(1)丂斀幩嬀傾儞僥僫偼丄斀幩嬀柺傊偺揹攇偺徠幩暘晍傪曄偊偰奐岥仩A傊偺徠幩儗儀儖傪彫偝偔偟偨傝丄庡斀幩嬀偺夞傝偵仩B傪梡偄偨幷暳斉傪庢傝晅偗偰丄僗僺儖僆乕僶乕偵傛傞僒僀僪儘乕僽傪寉尭偱偒傞丅
(2)丂僆僼僙僢僩僷儔儃儔傾儞僥僫媦傃仩C傾儞僥僫偼堦師曻幩婍媦傃偙傟傜偺巟帩拰側偳偑揹攇捠楬忋偵柍偄偺偱丄偙傟傜偵傛傞僽儘僢僉儞僌傗嶶棎偑柍偔丄僒僀僪儘乕僽摿惈偑椙偄丅
| A | B | C |
|---|
| 1 | 拞怱晹 | 媧廂嵽 | 儂乕儞儗僼儗僋僞 |
| 2 | 拞怱晹 | 斀幩嵽 | 僌儗僑儕傾儞 |
| 3 | 拞怱晹 | 媧廂嵽 | 僌儗僑儕傾儞 |
| 4 | 廃曈晹 | 斀幩嵽 | 僌儗僑儕傾儞 |
| 5 | 廃曈晹 | 媧廂嵽 | 儂乕儞儗僼儗僋僞 |
丂怴栤偺傛偆側婥偑偟傑偡偑丄偦偙偼姩偲姶妎偱僇僶乕偱偡丅
丂傑偢仩A丅崱夞偼僒僀僪儘乕僽傪彮側偔偡傞偲偄偆栤戣偱偡丅斀幩嬀傾儞僥僫偵揹攇傪徠幩偡傞偲偒丄拞怱偵偁偰傟偽偄偄曽岦偵斀幩偟偰偄偒偦偆偱偡偑丄廃曈偵揹攇傪徠幩偡傞偲丄側傫偐偳偭偐偄傜側偄偲偙傠偵旘傫偱偄偭偪傖偄偦偆偱偡丅偟偨偑偭偰仩A偼乽廃曈晹乿偐側乕偲巚偄傑偡丅
丂仩B丅媧廂嵽傪偮偗傟偽僒僀僪儘乕僽傪媧廂偟偰偔傟偦偆偱偡偑丄庡斀幩嬀偺廃傝偵斀幩嵽傪偮偗偨傜丄偄傜側偄曽岦偵揹攇偑旘傫偱僒僀僪儘乕僽傪嶌偭偰偟傑偄偦偆偱偡丅偟偨偑偭偰丄仩B偼乽媧廂嵽乿偩傠偆偲巚偄傑偡丅
丂仩C丅傾儞僥僫偺宍傪抦傜側偄偲懯栚偱偡丅僌儗僑儕傾儞偼偄偄偲偟偰丄儂乕儞儗僼儗僋僞傾儞僥僫偺宍偼抦偭偰偍偔傋偒偱偟傚偆丅
丂僒僀僪儘乕僽偑彫偝偄丅奐岥岠棪偑戝偒偄丅捈慄曃攇丄墌曃攇偵巊梡偱偒傞丅
丂尒傞偐傜偵丄乽堦師曻幩婍媦傃偙傟傜偺巟帩拰側偳偑揹攇捠楬忋偵柍偄乿偱偡丅偟偨偑偭偰仩C偼儂乕儞儗僼儗僋僞傾儞僥僫偱偡丅摎偊偼丄5偱偡丅
儊僀儞儘乕僽偲僒僀僪儘乕僽偲僶僢僋儘乕僽
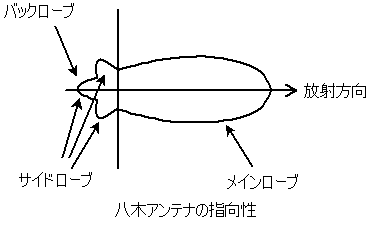
丂栚揑偺曽岦傊偺曻幩價乕儉偱嵟戝偺傕偺傪儊僀儞儘乕僽丄偦傟偲偼斀懳偺曽岦偵惗偠傞晄梫側曻幩傪僒僀僪儘乕僽丄僒僀僪儘乕僽偺拞偱嵟戝偺傕偺傪僶僢僋儘乕僽偲屇傇丅
丂儊僀儞儘乕僽偲僶僢僋儘乕僽偲偺斾傪偲偭偨傕偺傪FB(Front/Back)斾偲尵偄丄僨僔儀儖(dB)偱昞帵偡傞丅
丂FB=20log(儊僀儞儘乕僽嵟戝抣/僶僢僋儘乕僽嵟戝抣)
A-13丂師偺婰弎偼丄恾偵帵偡僿儕僇儖傾儞僥僫偺曻幩儌乕僪偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪偺惓偟偄慻傒崌傢偣傪壓偺斣崋偐傜慖傋丅
 (1)丂傊儕僢僋僗偺僺僢僠妏偑10乣15搙偱丄偦偺廃偑栺仩A偺帪丄揹攇傪傊儕僢僋僗偺幉曽岦傊曻幩偡傞偺偱丄幉儌乕僪曻幩偲偄偆丅
(1)丂傊儕僢僋僗偺僺僢僠妏偑10乣15搙偱丄偦偺廃偑栺仩A偺帪丄揹攇傪傊儕僢僋僗偺幉曽岦傊曻幩偡傞偺偱丄幉儌乕僪曻幩偲偄偆丅
(2)丂傊儕僢僋僗偺慡挿偑1攇挿掱搙埲壓偱丄偦偺廃偑1攇挿偵斾傋偰仩B偲偒丄揹攇傪傊儕僢僋僗幉偵捈妏側柺撪傊曻幩偡傞偺偱丄悅捈儌乕僪乮僟僀億乕儖儌乕僪乯曻幩偲偄偆丅
(3)丂傊儕僢僋僗偺廃偑1.5攇挿掱搙偺帪丄枖偼傊儕僢僋僗偺僺僢僠偑1攇挿傪墇偊傞偲偒側偳偼丄揹攇傪傊儕僢僋僗幉曽岦媦傃懁曽岦僿曻幩偡傞偺偱仩C儌乕僪曻幩偲偄偆丅
| A | B | C |
|---|
| 1 | 敿攇挿 | 戝偒偄 | 懡儘乕僽 |
| 2 | 1攇挿 | 彫偝偄 | 懡儘乕僽 |
| 3 | 敿攇挿 | 彫偝偄 | 懡儘乕僽 |
| 4 | 1攇挿 | 彫偝偄 | 悈暯 |
| 5 | 敿攇挿 | 戝偒偄 | 悈暯 |
丂僿儕僢僋僗傾儞僥僫偺栤戣偼愄偼傛偔弌偰偨偺偱偡偑丄嵟嬤偱偰側偐偭偨偲巚偄傑偡丅傂偝偟傇傝偵尒傑偟偨丅
丂壗傕抦傜側偔偰傕暘偐傝偦偆側偺偼仩C偱偡丅乽僿儕僢僋僗幉曽岦媦傃懁曽岦傊曻幩乿偡傞偺偱丄懡儘乕僽偐側乕偲巚偄傑偡丅偳偆峫偊偰傕乽悈暯乿曽岦偩偗偵揹攇傪旘偽偟偰偄側偄偱偡丅偙傟偱1乣3偵峣傟傑偡丅
丂師偵仩B偱偡丅(3)偵偍偄偰乽僿儕僢僋僗偺廃偑1.5攇挿掱搙偺帪乿偺榖傪偟偰偄傑偡丅偱丄(2)偱偼丄僿儕僢僋僗偺廃偑1攇挿傛傝戝偒偄偐彫偝偄偐傪栤戣偵偟偰偄傑偡丅1攇挿傛傝戝偒偄偲1.5攇挿偵側傞偙偲傕偁傞偺偱丄乽戝偒偄乿偲偄偆摎偊偼峫偊偵偔偄偱偡丅偟偨偑偭偰丄仩B偼彫偝偄偱偡丅
丂嵟屻偵仩A偱偡偑丄夁嫀栤偵偼傛偔弌偰傑偟偨丅栺1攇挿偱偡丅僿儕僢僋僗偲尵偭偨傜1攇挿偲妎偊偰偍偄偰懝偼側偄偲巚偄傑偡丅
丂摎偊偼2偱偡丅
A-14丂揹棧憌偺嵟戝揹巕枾搙偑3.6亊1011[屄/m3]偺偲偒偺椪奅廃攇悢偺抣偲偟偰丄嵟傕嬤偄傕偺傪壓偺斣崋偐傜慖傋丅偨偩偟丄揹棧憌偺揹巕枾搙傪N[屄/m3]丄僾儔僘儅偺廃攇悢傪f[Hz]媦傃揹攇偺孅愜棪傪n偲偡傟偽丄師幃偺娭學偑偁傞丅
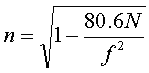
1丂5.4[MHz]丂
2丂8.6[MHz]丂
3丂10.8[MHz]丂
4丂12.2[MHz]丂
5丂16.2[MHz]
丂偙偺栤戣偼傛偔弌傑偡丅偑丄抣傕幃傕梌偊傜傟傞偙偲偑懡偄偺偱丄偦偺応偱峫偊傟偽偄偄偲巚偄傑偡丅
丂暘偐偭偰偄傞偺偼N偱偡偺偱丄偙傟偼傑偢幃偵戙擖偟傑偡丅暘偐傜側偄抣偼f偲n偱偡丅崱夞偺栤戣偼廃攇悢傪抦傝偨偄偺偱嵟廔揑偵媮傔傞偺偼f偵側傝傑偡丅偲偡傞偲丄屻偼n偑暘偐傟偽OK偱偡丅椪奅廃攇悢偲偄偆偺偼揹棧憌傪撍偒敳偗偰偄偭偪傖偆廃攇悢偺偙偲偱偡丅偟偨偑偭偰椪奅廃攇悢偲偄偆偺偼揹棧憌偱孅愜偟側偄廃攇悢偲偄偆偙偲偱偡丅傑偭偨偔孅愜偟側偄帪偺孅愜棪偼0偱偡丅偟偨偑偭偰丄0=80.6N/f2偲側傛偆側f傪媮傔傟偽OK偱偡丅摎偊偼丄1偱偡丅
丂乽傑偭偨偔孅愜偟側偄帪偺孅愜棪偼0乿偲偄偆偺傪抦傜側偔偰傕宱尡偑偁傟偽偄偗傑偡丅乽側傫偲偐棪乿偲尵偭偨応崌丄偦偺抣偼乽0乣1乿丄乽1乣柍尷戝乿偺抣傪偲傝傑偡丅偙傟偼偍栺懇偱偡丅偱丄崱夞丄n傪1偲偐柍尷戝偵偡傞傛偆側f傪寛傔傞偙偲偼柍棟偱偡丅偟偨偑偭偰丄乽偁乕丄n偼懡暘0偩傠偆側乕乿偲巚偄傑偡丅
A-15丂嫍棧25[km]偺儅僀僋儘攇屌掕捠怣夞楬偵偍偄偰丄廃攇悢偑12[GHz]偱憲怣婡弌椡偑36[dBm]偺偲偒偺庴怣婡擖椡偺抣偲偟偰丄嵟傕嬤偄傕偺傪壓偺斣崋偐傜慖傋丅偨偩偟丄憲怣媦傃庴怣傾儞僥僫偺棙摼傪偦傟偧傟50[dB]媦傃51[dB]丄憲怣懁媦傃庴怣懁偺媼揹夞楬偺懝幐傪偦傟偧傟5[dB]媦傃6[dB]偲偟丄戝抧媦傃揱斃楬廃曈偺斀幩暔懱偐傜偺塭嬁偼側偄傕偺偲偡傞丅傑偨log10兾佮0.5偲偡傞丅
1丂-16[dBm]丂
2丂-10[dBm]丂
3丂3[dBm]丂
4丂20[dBm]丂
5丂44[dBm]
丂偪傚偭偲柍慄偺尰応傪抦偭偰偄傞恖娫偱偡偲丄傑偢4偲5偼偁傝摼側偄丄3傕夦偟偄丅1偐2偑懨摉偩傠偆側偲巚偄傑偡丅
丂堦斒偺曽偱傕憲怣婡弌椡偑36[dBm]側偺偵丄庴怣偱44[dBm]傕庢傝弌偣傞傢偗偑側偐傠偆偲慺杙巚偆偱偟傚偆丅
丂偦傟偼偦傟偲偟偰丄偙偺栤戣偼棨媄偺栤戣偱偼側偔堦棨摿僋儔僗偺偲偭偰傕娙扨側栤戣偱偡丅儃乕僫僗栤戣偱偡丅偙偺掱搙偺栤戣偼偝傜偭偲夝偗傞傛偆偵側偭偰偔偩偝偄丅
帺桼嬻娫揱斃懝幐儭
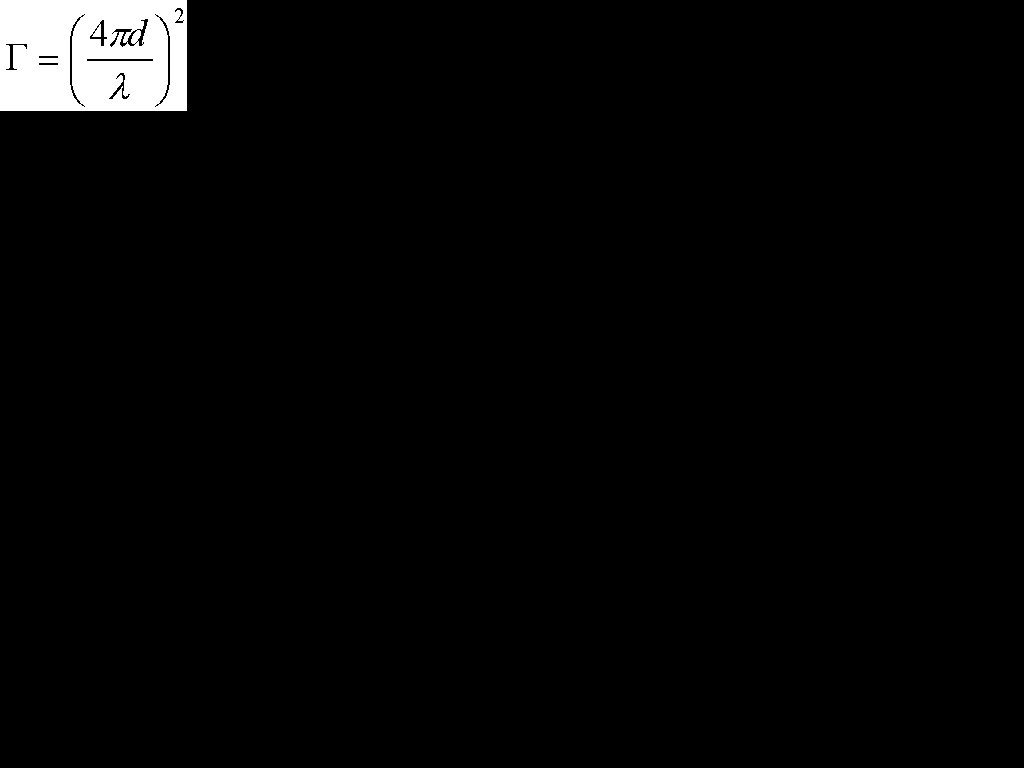
丂儭乵扨埵側偟乶乮帺桼嬻娫揱斃懝幐乯丂d乵m]乮嫍棧乯丂兩[m]乮攇挿乯
丂儭偼dB偵側偍偟偰巊梡偡傞偙偲偑懡偄偱偡丅偦偺帪偼丄10log10儭偱偡丅
丂偙偺幃傪尒偰暘偐傞偙偲偼丄揱斃懝幐偼嫍棧偺2忔偵斾椺偟偰憹偊偰乮梫偡傞偵嫍棧偑憹偊傞偲懝幐偼憹偊傞丄摉偨傝慜偩偗偳乯丄攇挿偺2忔偵斀斾椺偟偰懝幐偼憹偊傞乮梫偡傞偵攇挿偑挿偗傟偽挿偄傎偳懝幐偑彫偝偄乯丅
丂偲偙傠偱丄10log儭亖10log(4兾d/兩) 2傪寁嶼偡傞偺偼廃攇悢偐傜攇挿傪媮傔偨傝兾偑偁傞偺偱丄3.14傪偐偗嶼偟偨傝偲戝曄偱偡丅埲壓偵帵偡嬤帡幃傪巊偆偲寁嶼偑妝偐傕偟傟傑偣傫丅偍岲傒偱偍巊偄壓偝偄丅
丂儭[dB]亖32.4亄20logf亄20logd
丂丂f[MHz]乮廃攇悢乯丂d[km]乮嫍棧乯
丂偙偺幃偼捗杮仐垽抦導偝傫偵嫵偊偰偄偨偩偒傑偟偨丅
僨僔儀儖寁嶼偺応崌
丂Ps[dB]=Pt[dB]+Gs[dB]+Gt[dB]-儭[dB]
丂庴怣揹椡=憲怣揹椡+憲怣傾儞僥僫偺棙摼+庴怣傾儞僥僫偺棙摼-帺桼嬻娫揱斃懝幐
恀悢寁嶼偺応崌
丂Ps=Pt亊Gs亊Gt亐儭
丂庴怣揹椡=憲怣揹椡亊憲怣傾儞僥僫偺棙摼亊庴怣傾儞僥僫偺棙摼亐帺桼嬻娫揱斃懝幐
丂傑偢崱夞偼dB偱寁嶼偟偰偄傞偺偱丄帺桼嬻娫揱斃懝幐傪dB偱媮傔傑偡丅
丂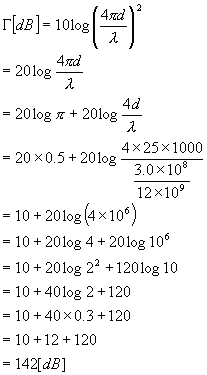
丂偁偲偼懌偟嶼偲堷偒嶼偱偡丅
丂庴怣婡擖椡亖憲怣婡弌椡亄傾儞僥僫偺棙摼亅媼揹慄偺懝幐亅帺桼嬻娫揱斃懝幐
丂庴怣婡擖椡亖36亄50亄51亅5亅6亅142亖-16[dBm]
A-16丂師偺婰弎偼丄崀塉媦傃戝婥拞偵晜梀偡傞悈揌傗昘愥偵傛傞SHF懷媦傃EHF懷偺揹攇偺尭悐偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋帤嬪偺惓偟偄慻傒崌傢偣傪壓偺斣崋偐傜慖傋丅
(1)丂柖傗嵶偐偄塉側偳偺傛偆偵丄攇挿偵斾傋偰廫暘彫偝偄捈宎偵悈揌偵傛傞尭悐偼丄庡偵媧廂偵傛傞傕偺偱偁傝丄偦偺戝偒偝偼仩A偺2忔媦傃扨埵柺愊偺嬻婥拞偵娷傑傟傞悈暘偺検偵斾椺偡傞丅
(2)丂悈揌偺捈宎偑柖傗嵶偐偄塉側偳傛傝戝偒偔側傞偲丄媧廂偺懠偵仩B偵傛傞尭悐偑惗偢傞丅
(3)丂昘偱偱偒偨塤傗姡憞偟偨愥偺仩C懝偼丄悈偵斾傋偰偐側傝彫偝偄偺偱棻巕偑廫暘彫偝偗傟偽丄偦偺尭悐偼堦斒偵柍帇偱偒傞丅
| A | B | C |
|---|
| 1 | 攇挿 | 嫟柭 | 摫懱 |
| 2 | 廃攇悢 | 嶶棎 | 摫懱 |
| 3 | 廃攇悢 | 嶶棎 | 桿揹懱 |
| 4 | 攇挿 | 嶶棎 | 桿揹懱 |
| 5 | 攇挿 | 嫟柭 | 桿揹懱 |
丂偙偺塉丄愥偺尭悐偵娭偡傞栤戣偼堦棨摿偵偼傛偔弌偰偄偨傛偆側婥傕偟傑偡丅
丂偁傫傑傝壗傕抦傜側偔偰傕弌棃偦偆側偺偼仩C丅愥偼摫懱偠傖側偄偺偱丄桿揹懱懝偐側偁偲巚偄傑偡丅
丂師偵仩B丅柍慄偺悽奅偵乽嫟柭乿偲偄偆尵梩偼弌偰偒傑偣傫丅傑偨嫟柭偟偰尭悐偑婲偙傞偭偰偺偼丄側傫偲側偔峫偊傜傟傑偣傫丅嫟柭偟偨傜丄側傫偐揹攇偑僷儚乕傾僢僾偟偦偆偱偡丅偟偨偑偭偰仩B偼嶶棎偱偡丅
丂仩A偼廃攇悢偱偡丅婎杮揑偵廃攇悢偑崅偄傎偳丄偁傜備傞傕偺偵娭偟偰尭悐偑戝偒偄偲峫偊偰娫堘偄側偄偱偡丅摫懱懝傕帺桼嬻娫揱斃懝幐傕廃攇悢偑崅偄曽偑尭悐偑寖偟偄偱偡丅
丂摎偊偼3偱偡丅
A-17丂師偺婰弎偼僼儗僱儖僝乕儞偵偮偄偰弎傋偨傕偺偱偁傞丅偙偺偆偪岆偭偰偄傞傕偺傪壓偺斣崋偐傜慖傋丅偨偩偟丄憲怣揰傪T丄庴怣揰傪R偲偟丄捈慄TR偵捈妏側忈暻暯柺傪峫偊丄偙偺柺偲捈慄TR偲偑岎傢傞揰O傪拞怱偵偟偨墌宍偺憢倵倫奐偗丄偦偺墌廃忋偺擟堄偺堦揰傪捠傞揹攇捠楬傪TAR偲偡傞丅
 1丂TAR偲TR偲偺捠楬嵎偑敿攇挿埲壓偲側傞嬻娫傪丄戞堦僼儗僱儖僝乕儞偲尵偆丅
1丂TAR偲TR偲偺捠楬嵎偑敿攇挿埲壓偲側傞嬻娫傪丄戞堦僼儗僱儖僝乕儞偲尵偆丅
2丂T媦傃R偼丄戞堦僼儗僱儖僝乕儞偺撪懁偵偁傞丅
3丂TAR偲TR偲偺捠楬嵎偑敿攇挿偺婏悢攞偺偲偒丄R偵偍偗傞揹奅嫮搙偼丄忈暻偑側偄偲偒偺揹奅嫮搙偺2攞偱偁傞丅
4丂TAR偲TR偺捠楬嵎偑敿攇挿偺嬼悢攞偺偲偒丄R偵偍偗傞揹奅嫮搙偼丄忈暻偑側偄偲偒偺揹奅嫮搙偵摍偟偄丅
5丂僼儗僱儖僝乕儞偺嫬奅柺偼丄T媦傃R傪擇偮偺徟揰偲偡傞夞揮懭墌懱柺偱偁傞丅
丂僼儗僱儖僝乕儞偲偄偊偽妎偊偰偍偔偙偲偼彮側偔偰丄乽戞堦僼儗僱儖僝乕儞偵忈奞暔偑偁偭偪傖懯栚乿乽戞堦僼儗僱儖僝乕儞偼捠楬嵎偑兩/2偵側傞撪懁偺椞堟乿乽戞堦僼儗僱儖僝乕儞偼懭墌宍乿偔傜偄偱偡丅
丂偝偰丄岆傝偼偳傟偐偲偄偆栤戣偺応崌丄摨偠傛偆側暥復偱抣偲偐尵梩偑堘偆偙偲偑偁傞応崌偼丄偦偺偳偪傜偐偑岆傝偱偁傞壜擻惈偑崅偄偱偡丅偙偺栤戣偺応崌丄3偲4偵側傝傑偡丅屻偼塣偱偡丅
丂摎偊偼4偱偡丅巹偼娫堘偊傑偟偨丅偭偰偄偆偐僼儗僱儖僝乕儞偺堄枴傪抦傝傑偣傫偱偟偨丅
丂偙偙偐傜偼塕偑彂偄偰偁傝傑偡丅怣偠側偄偱壓偝偄丅
丂庤帩偪偵揹攇揱斃偵娭偡傞杮偑側偄偺偱側傫偲傕尵偊側偄偺偱偡偑巹側傝偺夝庍傪乮梫偡傞偵偄偄壛尭偭偰偙偲偱偡丅乯丅
丂巹偼嵟弶乽揱斃楬偺嵎偑兩/2偩偭偨傜偦偺揹攇摨巑偼埵憡偑媡偵側傞偺偱0偵側傞乿傫偠傖側偄偐偲巚偄傑偟偨丅偱傕丄偦傟偼乽捈愙攇偲斀幩攇乿偺帪偵栤戣偵側傞傫偱偁偭偰丄崱夞偺僼儗僱儖僝乕儞偼傑偭偨偔堘偆傒偨偄偱偡丅
丂揹攇偼偁傞掱搙偺傂傠偑傝傪帩偭偰嬻娫傪揱傢傞傛偆偱偡丅揹攇傪弌偟偨偲偒丄憲怣揰偲庴怣揰偺娫偵忈暻偑偁偭偰偦傟偵捈宎1mm偺寠偑偁偄偰傞傛偆忬懺偩偲丄偦偺1mm偺寠暘偟偐揹攇偑揱傢傜側偄傛偆偱偡丅偠傖偁丄偙偺捈愙攇傪慡晹揱偊傞偵偼偳偺掱搙偺戝偒偝偺寠偑偁偄偰偄傟偽偄偄傫偩傠偆偐偲寁嶼偟偰弌偟偨偺偑戞堦僼儗僱儖僝乕儞傒偨偄偱偡丅
丂師偵戞擇僼儗僱儖僝乕儞丅偙傟偼揹攇傪庛傔傑偡丅側傫偱庛傔傞偺偐偼傢偐傜側偄偱偡丅戞嶰僼儗僱儖僜乕儞傪捠偭偰偒偨揹攇偼揹攇傪嫮傔傑偡乮側傫偱偐偼暘偐傜側偄偱偡乯丅摨偠傛偆偵丄戞巐僼儗僱儖僝乕儞偼丒丒丒丅戞擇僼儗僱儖僝乕儞埲崀傪捠偭偰偔傞揹攇偼夞愜攇側偺偱丄捈愙攇傛傝庛偄偱偡丅偦偟偰丄偦傟偼戞仜僼儗僱儖僝乕儞偺仜偺悢帤偑戝偒偔側傟偽側傞傎偳丄偨偔偝傫夞愜偟側偄偲庴怣揰偵偨偳傝拝偗側偄偺偱揹攇偼庛偔側偭偰偄偒傑偡丅偱丄寢嬊戞堦僼儗僱儖僝乕儞傪揱傢偭偰偒偨揹攇偐傜戞柍尷戝僝乕儞傑偱揱傢偭偰偒偨揹攇傪懌偡偲丄杔傜偑偄偮傕巊偭偰偄傞乽庴怣揹奅嫮搙乿偵側傞傒偨偄偱偡丅擄偟偄偱偡偹丄揹攇偼丅扤偐杮摉偺偲偙傠傪嫵偊偰偔偩偝偄丅
A-18丂旝彫僟僀億乕儖傾儞僥僫偺傛偆偵攇挿偵斾傋偰廫暘彫偝側傾儞僥僫偺應掕傪偡傞偲偒丄曻幩揹奅偵懳偡傞桿摫揹奅偺塭嬁偵傛傞岆嵎傪8%埲壓偲偡傞偨傔偵昁梫側憲怣傾儞僥僫偲庴怣傾儞僥僫娫偺嵟彫應掕嫍棧偺抣偲偟偰嵟傕嬤偄傕偺傪壓偺斣崋偐傜慖傋丅偨偩偟丄攇挿傪兩[m]偲偡傞丅
1丂兩/2[m]
2丂兩[m]
3丂2兩[m]
4丂5兩[m]
5丂10兩[m]
丂妋偐夁嫀栤偵偁傝傑偟偨丅妎偊偰偄側偒傖偱偒傑偣傫丅摎偊偼2兩偱偡丅
丂偙傟偩偲枴婥側偄偲偐擺摼偺峴偐側偄曽偺偨傔偵摫弌傪帵偟傑偡丅
丂傑偢丄旝彫僟僀億乕儖傾儞僥僫偺嫍棧r偵偍偗傞揹奅偺幃傪抦傜側偄偲懯栚偱偡丅偪側傒偵偙偺幃傪妎偊偰偄傞昁梫偼傑偭偨偔偁傝傑偣傫丅
旝彫僟僀億乕儖傾儞僥僫偺嫍棧r偵偍偗傞揹奅乮妎偊偰偄傞偲偆傟偟偄乯

丂俤 [V乛m]乮揹奅乯丂r [m]乮嫍棧乯
丂偙偺幃帺懱偼妎偊側偄偱丄曻幩揹帴奅偼嫍棧r偵斀斾椺偟偰桿摫揹帴奅偭偰偺偼嫍棧r偺2忔偵斀斾椺偡傞傫偩側偭偰偙偲偲丄嫍棧r偑戝偒偄偲桿摫揹帴奅偲惷揹奅偼嫍棧偺2忔偲偐3忔偵斾椺偡傞偺偱柍帇偟偰偄偄偙偲傪妎偊偰偍偗偽偍偭偗乕偱偡丅
丂曻幩揹奅偵懳偡傞桿摫揹奅偺塭嬁偵傛傞岆嵎傪8%偵偟偨偄偺偱偡偐傜丄曻幩揹奅亊0.08亖桿摫揹奅偵側傟偽OK偱偡丅偟偨偑偭偰
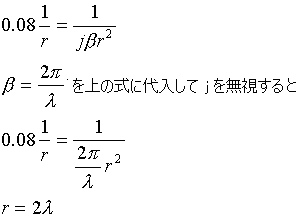
偱摎偊偼2兩偱偡丅夁嫀偵偙偺栤戣偑弌偨帪偼丄偪傖傫偲旝彫僟僀億乕儖傾儞僥僫偺揹奅嫮搙偺幃偑梌偊傜傟偰傑偟偨丅
A-19丂師偺婰弎偼丄傾儞僥僫宯偺嶨壒壏搙傪應掕偡傞曽朄偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪偺惓偟偄慻傒崌傢偣傪壓偺斣崋偐傜慖傋丅
 (1)丂恾偵帵偡峔惉偵偍偄偰丄摫攇娗僗僀僢僠傪昗弨嶨壒尮懁偵偡傞丅昗弨嶨壒尮傪摦嶌偝偣側偄偲偒丄幒壏偺嶨壒壏搙T0[K]偵斾椺偟偨擬嶨壒偑庴怣婡偵擖傝丄傑偨丄摦嶌偝偣偨偲偒丄昗弨嶨壒尮偺嶨壒壏搙TN[K]偵斾椺偟偨嶨壒偑庴怣婡偵擖傞丅
(1)丂恾偵帵偡峔惉偵偍偄偰丄摫攇娗僗僀僢僠傪昗弨嶨壒尮懁偵偡傞丅昗弨嶨壒尮傪摦嶌偝偣側偄偲偒丄幒壏偺嶨壒壏搙T0[K]偵斾椺偟偨擬嶨壒偑庴怣婡偵擖傝丄傑偨丄摦嶌偝偣偨偲偒丄昗弨嶨壒尮偺嶨壒壏搙TN[K]偵斾椺偟偨嶨壒偑庴怣婡偵擖傞丅
丂偦傟偧傟偺嶨壒壏搙偵懳墳偡傞庴怣婡偺弌椡N0[W]偲NN[W]偺斾丄Y1偼丄師幃偱昞偝傟傞丅偨偩偟丄TR[K]偼丄掅嶨壒憹暆婍偺摍壙擖椡嶨壒偱偁傞丅
丂Y1亖N0乛NN亖仩A丂丒丒丒嘆
(2)丂摫攇娗僗僀僢僠傪傾儞僥僫懁偵偟偨偲偒偺庴怣婡弌椡偲昗弨嶨壒尮懁偵偟偰昗弨嶨壒尮傪摦嶌偝偣偨偲偒偺庴怣婡弌椡偲偺斾Y2偼丄傾儞僥僫宯偺嶨壒壏搙傪TA[K]偲偡傟偽(1)偲摨條偵偟偰師幃偱昞偝傟傞丅
丂Y2亖仩B丂丒丒丒嘇
(3)丂幃嘇偐傜丄TA偼丄師幃偲側傞丅
丂TA亖(TN亄TR)乛Y2亅仩C丂丒丒丒嘊
丂偟偨偑偭偰丄幃嘊偵幃嘆偐傜媮傔偨TR傪戙擖偡傟偽TA傪媮傔傞偙偲偑弌棃傞丅
| A | B | C |
|---|
| 1 | (TN亄TR)乛(T0亄TR) | (TN亄TR)乛(TA亄TR) | T0 |
| 2 | (T0亄TR)乛(TN亄TR) | (TN亄TR)乛(TA亄TR) | TR |
| 3 | (T0亄TR)乛(TN亄TR) | (TN亄TR)乛(TA亄TR) | T0 |
| 4 | (T0亄TR)乛(TN亄TR) | TN乛(TA亄TR) | TR |
| 5 | (TN亄TR)乛(T0亄TR) | TN乛(TA亄TR) | T0 |
丂抦幆偑側偔偰傕暘偐偭偰偟傑偆偍庤寉栤戣偱偡丅
丂傑偢丄仩C偲仩B偺摎偊偵拲栚偟傑偡丅幃嘇傪曄宍偡傞偲幃嘊偵側傞偲栤戣偵彂偄偰偁傝傑偡丅仩C偵擖傞慖戰巿偼T0偲TR偱偡丅幃嘇偺拞偵T0偼娷傑傟傑偣傫丅偟偨偑偭偰仩C偼TR偵側傝傑偡丅師偵仩B丅暘曣偵TR偑偁傞偐側偄偐偺堘偄偱偡丅偲偙傠偱TR偭偰偺偼壗偐偲偄偆偲丄掅嶨壒憹暆婍偺嶨壒偱偡丅仩A偺慖戰巿傪尒傞偲丄暘巕偵傕暘曣偵傕TR偑擖偭偰偄傑偡丅偦偟偰丄夞楬恾傪尒傞偲摫攇娗僗僀僢僠傪愗傝懼偊偰傕丄掅嶨壒憹暆婍傪捠傝傑偡丅偟偨偑偭偰TR偑偁傞曽偑懨摉偐偲巚傢傟傑偡丅偟偨偑偭偰摎偊偼2偱偡丅
丂栤戣暥偼挿偄偺偱偡偑丄夝摎偼10昩偱弌傑偡丒丒丒
丂傑偢仩A丅斀幩斅偺斀懳懁偵壗偑偁傞偐偲偄偆偙偲偱偡偑丄斀幩斅偼嬀偺揹攇僶乕僕儑儞偲峫偊偰OK偱偡丅揹攇傪斀幩斅偵敪幩偡傞偲偦偭偔傝偦偺傑傑婣偭偰偒傑偡丅偟偨偑偭偰丄斀幩斅偺偙偭偪懁偵傾儞僥僫偑偁傞偲斀幩斅偼嬀側傫偱偡偐傜丄斀幩斅偺岦偙偆懁偵傕摨偠傾儞僥僫偑偁傞偙偲偵側傝傑偡丅偟偨偑偭偰丄仩A偼嬀憸偱偡丅
丂師偵仩B丅曃攇偲敿抣暆偱偡偑丄崌傢偣傜傟傞偺偼曃攇偱偡丅敿抣暆偼傾儞僥僫偵屌桳偺傕偺側偺偱崌傢偣傜傟傑偣傫丅敿抣暆偲偄偆偺偼儊僀儞儘乕僽偺暆偺偙偲傪尵偄傑偡丅敿抣暆偼傾儞僥僫偵傛偭偰堘偄傑偡丅偙傟傪偳偆傗偭偰崌傢偣傞傫偱偟傚偆偐丒丒丒丅偱傕丄栤戣傪撉傓偲丄偳偭偪傕昗弨傾儞僥僫傪巊偭偰偄傞傒偨偄側偺偱丄敿抣暆偼摨偠側偺偐傕偟傟傑偣傫丅偠傖偁丄傕偲傕偲敿抣暆偼崌偭偰偄傞傢偗偱丄崱峏壗傪崌傢偣傞偺偐傢偐傝傑偣傫丅
丂摎偊偼1偱偡丅
丂B栤戣偼丄傑偢僌儖乕僾暘偗偱偡丅1偲6丄2偲7丄3偲10丄4偲8丄5偲9偱偡丅
丂傑偢仩傾丅兤傪0偵偡傞偐兾/2偵偡傞偐偱偡丅栤戣傪撉傓偲乽嵟戝抣偑1偲側傞乿偲彂偄偰偁傞偺偱丄側傫偲側偔D(兤)偑戝偒偗傟偽偄偄傫偩側偲巚偄傑偡丅 傪尒傞偲丄兤偵兾/2傪擖傟傞偲丄暘巕偺妵屖偺拞偼1偵側傝傑偡偑丄兤偵0傪擖傟傞偲丄妵屖偺拞偵n兾d/兩偑巆傝傑偡丅棨媄偺栤戣偱偼丄妵屖偺拞偑0偲偐1偵側傞偺偑戝掞惓夝偱偡丅偟偨偑偭偰摎偊偼兾/2偱偡丅
傪尒傞偲丄兤偵兾/2傪擖傟傞偲丄暘巕偺妵屖偺拞偼1偵側傝傑偡偑丄兤偵0傪擖傟傞偲丄妵屖偺拞偵n兾d/兩偑巆傝傑偡丅棨媄偺栤戣偱偼丄妵屖偺拞偑0偲偐1偵側傞偺偑戝掞惓夝偱偡丅偟偨偑偭偰摎偊偼兾/2偱偡丅
丂偙傟偱0傪慖傇偲丄暘巕偼d偲兩偵埶懚偡傞偙偲偵側傝傑偡丅偦偆偡傞偲丄乽偄偮偱傕嵟戝抣偑1乿偵偼側傜側偄婥偑偟傑偡丅側偺偱丄兾/2傪慖傇偺偑懨摉偱偡丅
丂師偵仩僀丅仩傾偱兾/2傪慖傃傑偟偨丅兾/2偼90搙偱偡丅偟偨偑偭偰丄仩僀偼捈妏偵側傝傑偡丅
丂仩僂偲仩僄丅抦傜側偄偲弌棃傑偣傫丅仩僂偼僽儘乕僪僒僀僪丄仩僄偼僄儞僪偩偦偆偱偡丅偙傟丄偲偒偳偒弌傞偺偱偡偑丄崱傑偱偼僿儕僇儖傾儞僥僫偺帪偔傜偄偟偐弌側偐偭偨婥偑偟傑偡丅
丂仩僆丅巜岦惈傪寛傔傞偺偱偡偐傜丄巜岦惈學悢偵寛傑偭偰傑偡丅
傾:3 僀:8 僂:2 僄:1 僆:9
B-2丂師偺婰弎偼丄恾偵帵偡僥儗價僕儑儞曻憲偺媼揹夞楬偵梡偄傜傟傞僴僀僽儕僢僪儕儞僌傪梡偄偨掕僀儞僺乕僟儞僗僲僢僠僟僀僾儗僋僒偵偮偄偰弎傋偨傕偺偱偁傞丅偙偺偆偪惓偟偄傕偺傪1丄岆偭偰偄傞傕偺傪2偲偟偰夝摎偣傛丅
傾丂僴僀僽儕僢僪儕儞僌偺C1偐傜擖椡偝傟偨塮憸怣崋偼仜3媦傃仜4偵怳暆偑摍偟偔埵憡嵎偑90搙偺怣崋偲偟偰尰傟傞丅
僀丂D偼丄夞楬偺晄惍崌晹暘偱惗偢傞塮憸怣崋媦傃壒惡怣崋偺斀幩攇媦傃摟夁攇傪媧廂偡傞偨傔偺媧廂掞峈偱偁傞丅
僂丂2屄偺R偼丄塮憸怣崋偺栺敿暘傪C1懁傊栠偡偨傔偺斀幩慺巕偱偁傞丅
僄丂壒惡怣崋偼丄僴僀僽儕僢僪儕儞僌C2偱塮憸怣崋偲崌惉偝傟偰傾儞僥僫傊憲傜傟傞偺偱丄揱憲楬L1媦傃L2偼捠夁偟側偄丅
僆丂仜6偵尰傟傞塮憸怣崋偲壒惡怣崋偺埵憡偑堦抳偟偰偄傞偺偱丄堦偮偺傾儞僥僫偐傜憲怣偝傟傞椉怣崋攇偺巜岦惈偼摨偠偵側傞丅
丂C1丄C2 : 僴僀僽僢僪儕儞僌
丂L1丄L2 : 揱憲楬
丂夁嫀栤偵椙偔弌偰偄傞栤戣側偺偱丄僷乕僼僃僋僩偵峴偒偨偄強偱偡丅
丂傾丅僴僀僽儕僢僪儕儞僌偺堦曈偼妋偐兩/2偱偡丅偦偺偨傔丄仜3偲仜4偵偺揹攇偼埵憡偑90搙偢傟偰偄傑偡丅偟偨偑偭偰惓夝偼仜偱偡丅
丂僀丅偙傟偼偦偺捠傝偱偡丅仜丅偙偙偱媧廂偟偰偁偘側偄偲丄懠偱媧廂偟偰偔傟傞掞峈偑偄傑偣傫丅
丂僂丅R偲尵偊偽掞峈偱偡丅掞峈偑斀幩慺巕偺傢偗側偄偺偱亊偱偡丅偮偄偱偵丄塮憸怣崋偼傾儞僥僫偵岦偐偭偰梸偟偄偺偵丄偙偙偱塮憸怣崋傪敿暘栠偡堄枴偼側偄偺偱丄傗偭傁傝亊偱偡丅
丂僄丅塮憸憲怣婡偐傜弌偨揹攇偑揱憲楬傪捠傞偺偵丄壒惡憲怣婡偐傜弌偨揹攇偑揱憲楬傪捠傜側偄傢偗側偄偺偱丄亊偱偡丅
丂僆丅壒惡偲塮憸偼巜岦惈偑摨偠偱側偄偲傑偢偄乮傑偢偄偱偡傛偹丒丒丒壒惡偺揹攇偑撏偄偰傞偺偵丄塮憸偺揹攇偑撏偐側偄偭偰偺偼乯偺偱丄仜偱偡丅
傾:1 僀:1 僂:2 僄:2 僆:1
丂壒惡怣崋偼偳偆傗偭偰傾儞僥僫偵峴偔偺偐朰傟傑偟偨丒丒丒R偺偲偙偱斀幩偡傞傫偩偭偨偐側丒丒丒
B-3丂師偺婰弎偼丄揹攇嶨壒偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪傪壓偺斣崋偐傜慖傋丅
(1)丂嬻揹嶨壒偼丄仩傾偵傛偭偰敪惗偡傞徴寕惈嶨壒偱偁傝丄庡偵愒摴抧懷偱敪惗偟偨屄乆偺徴寕惈嶨壒偑揹棧憌揱斃偵傛偭偰拞堒搙抧堟偱摓棃偟丄廳側傝崌偭偰楢懕惈嶨壒偲偟偰庴怣偝傟傞丅擔杮偵偍偗傞HF懷偺嬻揹嶨壒偺嫮搙偼丄仩僀偵傛傞尭悐偺側偄栭娫偺傎偆偑擔拞傛傝嫮偔側傞丅
(2)丂塅拡嶨壒偼丄懢梲埲奜偺峆惎偑敪偡傞嶨壒偱偁傝丄仩僂僿儖僣偐傜1僊僈僿儖僣偺斖埻偺捠怣偵塭嬁傪梌偊傞丅敪惗尮偼丄屄乆偺揹攇惎偲屇偽傟傞峆惎偺懠偵仩僄偵偁傝丄摿偵偦偺拞怱曽岦偑嫮偄丅
(3)丂懢梲嶨壒偼丄塅拡嶨壒偵斾傋偰戝偒偄偺偱丄塅拡捠怣摍偱偼仩僆傾儞僥僫偑懢梲偵岦偄偨偲偒偵戝偒側朩奞傪庴偗傞丅
1丂D憌丂
2丂庴怣丂
3丂2儊僈丂
4丂憲怣丂
5丂擬懷惈掅婥埑
6丂F憌丂
7丂揤懱丂
8丂嬧壨丂
9丂20儊僈丂
10丂棆曻揹
丂傛偔弌偰偒偦偆側栤戣偱偡偑丄旝柇偵堘偄傑偡偹丒丒丒
丂傑偢偼丄僌儖乕僾暘偗偱偡丅1偲6丄2偲4丄3偲9丄5偲10偱偡丅
丂傑偢傾丅徴寕惈側偺偱乽棆曻揹乿偐側偁偲巚偄傑偡丅
丂僀丅HF懷偺揹攇偑乽尭悐乿偡傞偺偼D憌偱偡丅F憌偼HF懷傪斀幩偟傑偡乮偦偺夁掱偱尭悐偟傑偡偑乯丅
丂僂丅妋偐崅偄廃攇悢偩偭偨傛側乕偲巚偭偨偺偱丄20儊僈傪慖傃傑偟偨丅摎偊偼20儊僈偱OK偱偡丅
丂僄丅栤戣偱乽塅拡嶨壒偼丄懢梲埲奜偺峆惎偢敪偡傞嶨壒乿偲彂偄偰偁傞偺偱丄揤懱側傢偗偑側偄偱偡丅偟偨偑偭偰丄摎偊偼嬧壨偱偡丅
丂僆丅嶨壒傪庴偗傞偺偼庴怣傾儞僥僫偺曽偱偡丅憲怣傾儞僥僫偱嶨壒偭偰偺偼傛偔傢偐傝傑偣傫丅
傾:10 僀:1 僂:9 僄:8 僆:2
B-4丂師偺婰弎偼丄峲嬻婡偺寁婍拝棨憰抲乮ILS乯偵梡偄傜傟傞儘乕僇儔僀僓偺傾儞僥僫偺曻幩僷僞乕儞偺惗惉尨棟偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪傪壓偺斣崋偐傜慖傋丅偨偩偟丄攇挿傪兩[m]偲偡傞丅
(1)丂恾1偵帵偡傛偆偵丄3屄偺斀幩斅晅悈暯敿攇挿僟僀億乕儖傾儞僥僫傪兩/2娫妘偱攝抲偟丄偙傟傪峲嬻婡偺恑擖僐乕僗偺墑挿慄忋偵慺巕偺挿偝曽岦偑墑挿慄偲捈妏偵側傞傛偆偵抲偔丅傾儞僥僫屄乆偺曻幩摿惈偼偡傋偰摨偠偱偁傝丄仩傾偱偁傞丅
(2)丂150僿儖僣偲90僿儖僣偱怳暆曄挷乮AM乯偟偨仩僀埵憡偺揹棳傪傾儞僥僫屄乆偵媼揹偡傞偲丄崌惉偺曻幩僷僞乕儞偼丄恾2偵帵偡傛偆偵丄慺巕偺挿偝曽岦偵捈妏側曽岦偱嵟戝偵側傞丅側偍丄揹奅偺埵憡偑婎弨偵懳偟偰僾儔僗乮亄乯90搙偵側傞傛偆偵丄媼揹揹棳偺埵憡偑寛傔傜傟偰偄傞丅偨偩偟丄揹攇偺揱斃帪娫偵傛傞埵憡偺抶傟傪柍帇偡傞傕偺偲偡傞丅
(3)丂斃憲攇偑梷埑偝傟偨150僿儖僣偲90僿儖僣偺懁懷攇揹棳傪仩僂偺傾儞僥僫偵180搙偺埵憡嵎偱媼揹偡傞偲丄崌惉偺曻幩僷僞乕儞偼丄恾3偵帵偡傛偆偵丄拞怱慄曽岦偑楇乮僰儖乯偺擇偮偺儘乕僽傪惗偢傞丅偙偺儘乕僽偺揹奅偺埵憡偼150僿儖僣懁懷攇偱偼塃懁偺儘乕僽偑亄90搙丄嵍懁偑儅僀僫僗乮亅乯90搙偲側傞傛偆偵媼揹揹棳偺埵憡偑寛傔傜傟偰偄傞丅90僿儖僣懁懷攇偱偼丄儘乕僽偺揹奅偺埵憡偑150僿儖僣懁懷攇偲媡偵側偭偰偄傞丅
(4)丂3屄偺傾儞僥僫偺崌惉偺曻幩僷僞乕儞偼丄(2)偵傛傞亄90搙偺埵憡傪帩偮揹奅偲(3)偵傛傞揹奅偺崌惉偱偁傞偺偱丄150僿儖僣懁懷攇偼丄拞怱慄偺仩僄偱摨憡偱壛傢傝崌偄丄仩僆偱偼媡憡偱憡嶦偝傟傞丅傑偨丄90僿儖僣懁懷攇偼丄150僿儖僣懁懷攇偲媡偵側傞丅斃憲攇偼曄傢傜側偄偺偱丄恾4偵帵偡傛偆側3庬椶偺曻幩僷僞乕儞偑摼傜傟傞丅
1丂堎側傞丂
2丂扨堦巜岦惈丂
3丂忋懁丂
4丂摨偠丂
5丂壓懁
6丂嵍塃丂
7丂憃曽岦惈丂
8丂嵍懁丂
9丂塃懁丂
10丂拞墰
丂嵟嬤峲嬻婡偺栤戣懡偄偱偡偹丒丒丒
丂傑偢丄僌儖乕僾傢偗丅1偲4丄2偲7丄3偲5偲8偲9丄6偲10偱偡丅
丂仩傾丅扨堦偐憃曽岦偱偡偑丄栤戣偺恾傪尒傞偲偳偆尒偰傕扨堦曽岦偱偡丅摎偊偼2偱偡丅
丂仩僀丅摨偠偐堎側傞偐偱偡丅堎側傞埵憡偲偡傞偲乽偠傖偁丄偳傫側埵憡偱傕偄偄傫偐偄丠乿偲媈栤偑惗偠傑偡丅偟偨偑偭偰丄摎偊偼摨憡偱偡丅
丂仩僂丅栤戣偺愭偺曽傪撉傓偲丄塃懁偺儘乕僽偑亄90搙丄嵍懁偺儘乕僽偑亅90搙偲偽偭偪傝彂偄偰偁傝傑偡丅摎偊偼嵍塃偱偡丅
丂仩僄偲仩僆丅偲偰傕擸傔傞偲偙傠偱偡丅塃懁偐嵍懁偑擖傞偺偼偡偖偵暘偐傞偲巚偄傑偡偑丄偳偭偪偑塃偱偳偭偪偑嵍偐丄偼抦傜側偄偲暘偐傝傑偣傫丅埵憡偺僀儊乕僕偑暒偗偽偄偄偺偱偡偑丄巹偵偼偦傟偼弌棃傑偣傫偱偟偨丅埵憡偑恑傫偱偄傞曽偵儘乕僽偑弌傞傒偨偄偱偡偹丅摎偊偼仩僄偑塃懁丄仩僆偑嵍懁偩偦偆偱偡丅
傾:2 僀:4 僂:6 僄:9 僆:8
B-5丂師偺婰弎偼丄傾儞僥僫娫偺攚柺寢崌搙偺應掕偵偮偄偰弎傋偨傕偺偱偁傞丅仩撪偵擖傟傞傋偒帤嬪傪壓偺斣崋偐傜慖傋丅
 (1)丂撈棫偟偨擇偮埲忋偺柍慄夞慄偑摨堦偺仩傾傪嫟梡偟丄傾儞僥僫偑揝搩忋偵愙嬤偟偰攚拞崌傢偣偵愝抲偝傟偰偄傞応崌側偳偺傾儞僥僫憡屳娫偺寢崌傪寢崌搙偲偄偆丅寢崌搙偼丄堦曽偺傾儞僥僫偵嫙媼偝傟偨仩僀偵懳偡傞懠曽偺傾儞僥僫偺弌椡揹椡偺斾偲偟偰掕媊偝傟傞丅
(1)丂撈棫偟偨擇偮埲忋偺柍慄夞慄偑摨堦偺仩傾傪嫟梡偟丄傾儞僥僫偑揝搩忋偵愙嬤偟偰攚拞崌傢偣偵愝抲偝傟偰偄傞応崌側偳偺傾儞僥僫憡屳娫偺寢崌傪寢崌搙偲偄偆丅寢崌搙偼丄堦曽偺傾儞僥僫偵嫙媼偝傟偨仩僀偵懳偡傞懠曽偺傾儞僥僫偺弌椡揹椡偺斾偲偟偰掕媊偝傟傞丅
(2)丂恾偵帵偡峔惉偼丄傾儞僥僫娫偺嫍棧傗憡懳揑側巜岦曽岦傪曄偊偰寢崌搙傪應掕偟丄婰榐偱偒傞傛偆偵偟偨傕偺偱偁傝丄怣崋敪惗婍偺弌椡傪Pt[dBm]丄庴怣婡偺擖椡傪Pr[dBm]丄憲怣懁媦傃庴怣懁偺媼揹夞楬偺懝幐傪偦傟偦傟Lt[dB]媦傃Lr[dB]偲偡傟偽丄寢崌搙C偼丄師幃偱昞偝傟傞丅
丂C亖仩僂丂[dB]
(3)丂寢崌搙偼旕忢偵仩僄偨傔丄怣崋敪惗婍偐傜偺怣崋偑庴怣懁傊捈愙怤擖偡傞偺傪杊偄偩傝丄摫攇娗偺仩僆側偳偐傜楻傟傪梷偊傞側偳丄應掕娐嫬偵拲堄偟側偗傟偽側傜側偄丅
1丂傾儞僥僫丂
2丂慡揹椡丂
3丂寢崌搙丂
4丂戝偒偄丂
5丂Pr亅Pt亄Lt亄Lr
6丂攚柺曽岦偺揹椡丂
7丂彫偝偄丂
8丂娗暻丂
9丂廃攇悢丂
10丂Pt亅Pr亄Lt亄Lr
丂柍慄偺忢幆傪抦偭偰偄傟偽暘偐傞偐側偁偲巚偄傑偡丅
丂傑偢丄僌儖乕僾暘偗丅1偲3偲8偲9丅2偲6丅4偲7丅5偲10丅
丂擖傝偦偆側尵梩偼傾儞僥僫偐娗暻偱偡丅撈棫偟偨擇偮埲忋偺柍慄夞慄偑偳偆傗偭偰傾儞僥僫傪嫟梡偟偰偄傞偺偐暘偐傜側偄偺偱丄娗暻偱偡丅
丂師偵仩僀丅慡揹椡偐攚柺曽岦偺揹椡偱偡偑丄攚柺曽岦偺揹椡偼偳偆傗偭偰應傞偺丠偲偄偆媈栤偲丄(2)偱乽怣崋敪惗婍偺弌椡傪Pt[dBm]乿偲偟偰偄傞偙偲偐傜丄慡揹椡偑惓夝偱偡丅
丂仩僂丅Pt[dBm]偑亅偐亄偐偭偰偙偲偱偡丅偊偊偲丄傛偔儅僀僋儘夞慄偵偍偄偰庴怣揹椡偼偄偔傜偱偟傚偆丠偲偄偆栤戣偺帪偼丄Lt偲Lr偼憲怣揹椡偐傜堷偒嶼偟傑偡丅偱丄崱夞偺栤戣偼懌偟嶼偟偰傑偡丅偲偄偆偙偲偼丄寢崌搙偺帪偼偡傋偰偺晞崋偑媡偵側傞偺偐側偁偲峫偊傑偡丅偟偨偑偭偰摎偊偼5偱偡丅
丂仩僄丅暥復傪傛乕偔撉傓偲暘偐傝傑偡丅怣崋敪惗婍偐傜庴怣懁傊揹椡偑夞傝崬傫偠傖偄偗側偄偭偰偙偲偼丄怣崋敪惗婍偺揹椡帺懱偑偲偰傕戝偒偄岆嵎偺梫場偵側傞偲偄偆偙偲偱偡丅怣崋敪惗婍偐傜庴怣懁偵捈愙夞傝崬傓揹椡偼偲偭偰傕彫偝偄偺偱丄岆嵎偺梫場偵偼側傜側偦偆偱偡偗偳丄偦傟偑岆嵎偺梫場偵側偭偪傖偆偭偰偙偲偼丄攚柺寢崌帺懱偺揹椡偑彫偝偄偭偰偙偲偱偡丅摎偊偼乽彫偝偄乿偱偡丅
丂仩僆丅娗暻偐傜楻傟傞傢偗偑側偄偺偱丄摎偊偼寢崌晹偱偡丅
傾:9 僀:2 僂:5 僄:7 僆:3



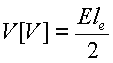

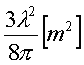

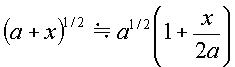 丒丒丒嘇
丒丒丒嘇

 偺偲偒丄
偺偲偒丄






 (1)丂傊儕僢僋僗偺僺僢僠妏偑10乣15搙偱丄偦偺廃偑栺仩A偺帪丄揹攇傪傊儕僢僋僗偺幉曽岦傊曻幩偡傞偺偱丄幉儌乕僪曻幩偲偄偆丅
(1)丂傊儕僢僋僗偺僺僢僠妏偑10乣15搙偱丄偦偺廃偑栺仩A偺帪丄揹攇傪傊儕僢僋僗偺幉曽岦傊曻幩偡傞偺偱丄幉儌乕僪曻幩偲偄偆丅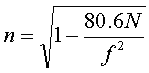
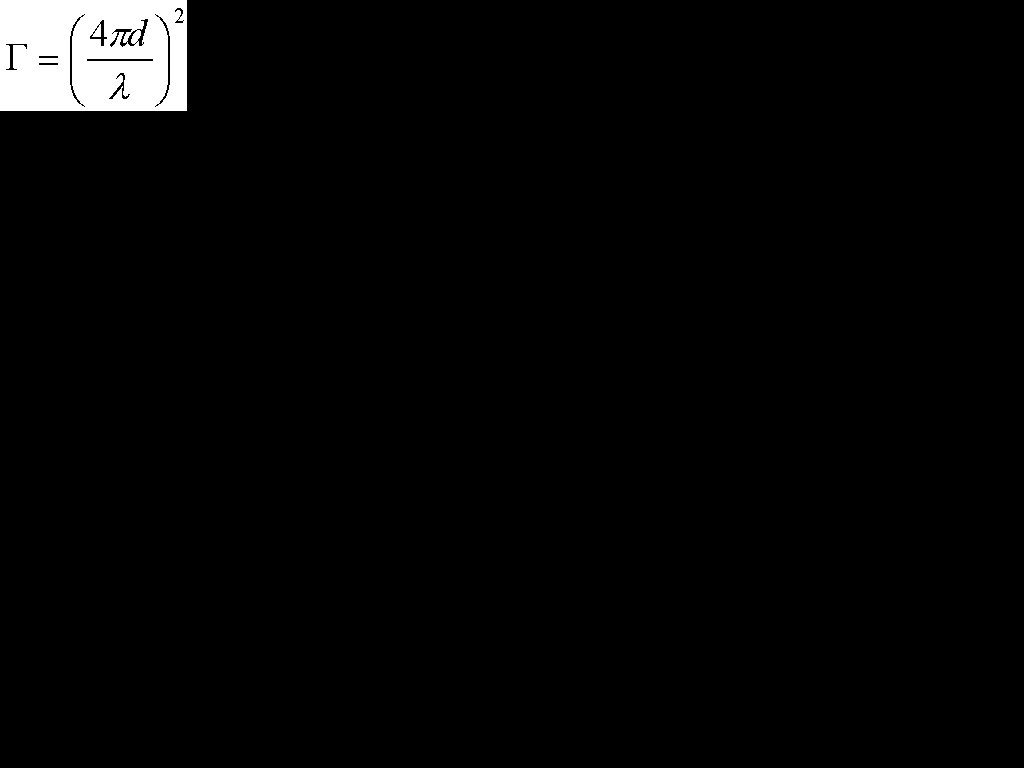
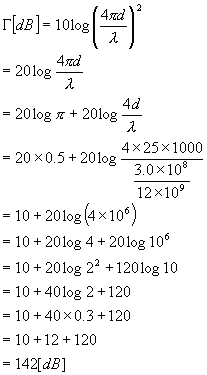


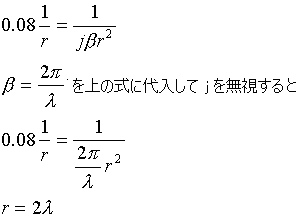
 (1)丂恾偵帵偡峔惉偵偍偄偰丄摫攇娗僗僀僢僠傪昗弨嶨壒尮懁偵偡傞丅昗弨嶨壒尮傪摦嶌偝偣側偄偲偒丄幒壏偺嶨壒壏搙T0[K]偵斾椺偟偨擬嶨壒偑庴怣婡偵擖傝丄傑偨丄摦嶌偝偣偨偲偒丄昗弨嶨壒尮偺嶨壒壏搙TN[K]偵斾椺偟偨嶨壒偑庴怣婡偵擖傞丅
(1)丂恾偵帵偡峔惉偵偍偄偰丄摫攇娗僗僀僢僠傪昗弨嶨壒尮懁偵偡傞丅昗弨嶨壒尮傪摦嶌偝偣側偄偲偒丄幒壏偺嶨壒壏搙T0[K]偵斾椺偟偨擬嶨壒偑庴怣婡偵擖傝丄傑偨丄摦嶌偝偣偨偲偒丄昗弨嶨壒尮偺嶨壒壏搙TN[K]偵斾椺偟偨嶨壒偑庴怣婡偵擖傞丅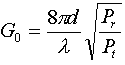
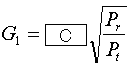
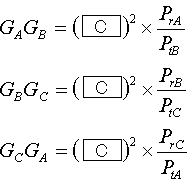
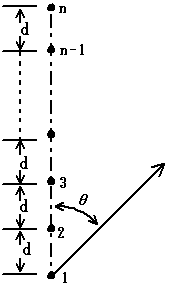 (1)丂恾偵帵偡傛偆偵丄n屄偺揰曻幩尮傪堦捈慄忋偵娫妘d[m]偱攝楍偟丄奺揰曻幩尮偺曻幩嫮搙偑摍偟偔丄偐偮摨憡偱偁傞偲偒偔偺攝楍學悢D(兤)偼丄師幃偱昞偝傟傞丅
(1)丂恾偵帵偡傛偆偵丄n屄偺揰曻幩尮傪堦捈慄忋偵娫妘d[m]偱攝楍偟丄奺揰曻幩尮偺曻幩嫮搙偑摍偟偔丄偐偮摨憡偱偁傞偲偒偔偺攝楍學悢D(兤)偼丄師幃偱昞偝傟傞丅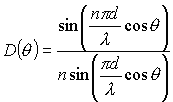
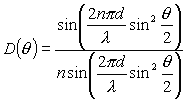


 (1)丂撈棫偟偨擇偮埲忋偺柍慄夞慄偑摨堦偺仩傾傪嫟梡偟丄傾儞僥僫偑揝搩忋偵愙嬤偟偰攚拞崌傢偣偵愝抲偝傟偰偄傞応崌側偳偺傾儞僥僫憡屳娫偺寢崌傪寢崌搙偲偄偆丅寢崌搙偼丄堦曽偺傾儞僥僫偵嫙媼偝傟偨仩僀偵懳偡傞懠曽偺傾儞僥僫偺弌椡揹椡偺斾偲偟偰掕媊偝傟傞丅
(1)丂撈棫偟偨擇偮埲忋偺柍慄夞慄偑摨堦偺仩傾傪嫟梡偟丄傾儞僥僫偑揝搩忋偵愙嬤偟偰攚拞崌傢偣偵愝抲偝傟偰偄傞応崌側偳偺傾儞僥僫憡屳娫偺寢崌傪寢崌搙偲偄偆丅寢崌搙偼丄堦曽偺傾儞僥僫偵嫙媼偝傟偨仩僀偵懳偡傞懠曽偺傾儞僥僫偺弌椡揹椡偺斾偲偟偰掕媊偝傟傞丅