2002年3月23日
一陸技
修正
A-7を利根のカッパさんの情報により修正しました。
比誘電率は0〜1の値を取ると思っていました。ごめんなさい。比誘電率は1から無限大の値をとります。
B-2の解答が間違っていたので解答と解説を訂正しました。
位相が遅れると波形は右にずれるんでした・・・
平成12年7月
A-1 次の記述は、受信アンテナの等価回路について述べたものである。□内に入るべき字句の正しい組合せを下の番号から選べ。
図1(a)に示すように、到来電波を受信したとき受信開放電圧がV0[V]のアンテナに任意の負荷Zl[Ω]を接続すると、電流I[A]が流れて負荷の端子電圧がVt[V]となる。このときの電磁界の状態は、図1(b)に示す到来電波の中で端子が開放されたアンテナの電磁界と、図1(C)に示す電圧V[V]を加えたとき電流I[A]が流れる入力インピーダンスZ[Ω]の送信アンテナとの合成であると考えることができる。
図1の関係が成立するためには、次の関係式が成立しなければならない。
V0−V=Vt=□A ・・・ ○1
○1式から負荷に流れる電流Iは、次式となる。
I=□B ・・・ ○2
○2式のV0は、□Cに関係するが、負荷には無関係である。したがって、受信アンテナは、図2に示すように、起電力がV0で、内部インピーダンスがZの電源と等価であると考えることができる。
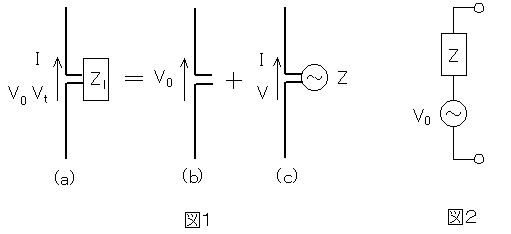
| A | B | C |
|---|
| 1 | IZl | V0/(Z+Zl) | 電流 |
|---|
| 2 | IZ | V0/2Z | 電流 |
|---|
| 3 | IZl | V0/2Z | 到来電波 |
|---|
| 4 | IZ | V0/2Z | 到来電波 |
|---|
| 5 | IZl | V0/(Z+Zl) | 到来電波 |
|---|
新問な気がしますが、図をじっと見れば自ずと答えが分かります。
まず□Aですが、IZlかIZを選びます。ここで図1の(c)を見ます。これを見るとどう見てもV=IZです。さらに図1の(a)を見るとどう見てもVt=IZlです。したがって、1か3か5しか選びようがありません。
次に□Bですが、□AですでにVt=IZlと分かっています。そしてV0−V=Vtですので、V0−V=IZlをI=の式になおすだけです。図1の(c)よりV=IZというのが分かるのでV0−V=IZlのVにIZを代入して計算するとV0/(Z+Zl)です。したがって、1か5を選びます。
最後に□Cですが、問題に「到来電波を受信したとき受信開放電圧がV0[V]」と書いてあります。ですから、V0は到来電波に関係するに決まっています。また「負荷Zl〔Ω〕を接続すると、電流I〔A〕が流れて」と問題文にあり、「V0は、□Cに関係するが、負荷には無関係である」ので、電流はV0に無関係と分かります。したがって答えは5です。
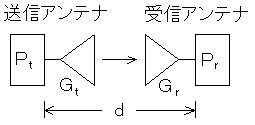
A-2 図に示すように、自由空間において、絶対利得がGt(真値)のアンテナから電波を送信し、これを距離d[m]離れた点で絶対利得がGr(真値)のアンテナで受信したときの受信有能電力(受信最大有効電力)がPr[W]であった。この時の送信電力Pt[W]を表す式として、正しいものを下の番号から選べ。ただし、電波の波長をλ[m]とする。
1 Pt=(4πd/λ)2Pr/GtGr 2 Pt=(λ/4πd)2Pr/GtGr 3 Pt=(4πd/λ)2GtGrPr 4 Pt=(λ/4πd)2GtGrPr 5 Pt=(2πd/λ)2GtGrPr
知らなきゃ出来ませんが、よく出る問題なので出来るようにしましょう。
自由空間伝搬損失Γ
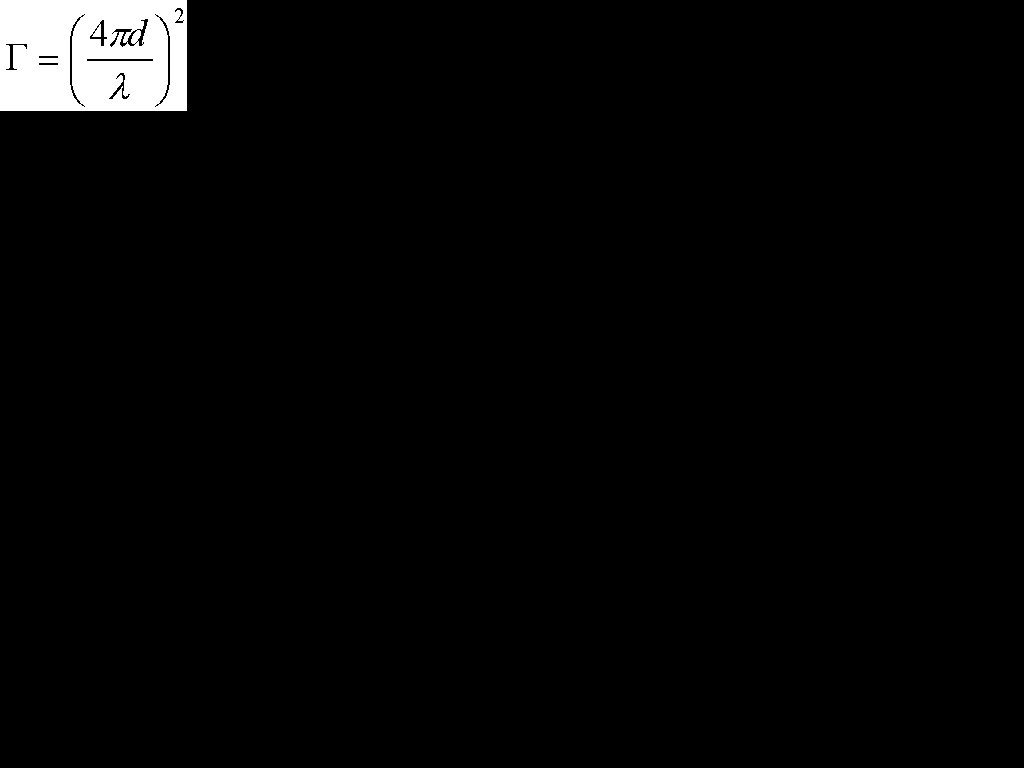
Γ[単位なし](自由空間伝搬損失) d[m](距離) λ[m](波長)
より、まず5番は違うことが分かります。次に、計算の単位がデシベルの場合
受信電力=送信電力+送信アンテナの利得+受信アンテナの利得-自由空間伝搬損失
です。でも、今回は真値です。真値の場合は+が×、-が÷になります。したがって、
受信電力=送信電力×送信アンテナの利得×受信アンテナの利得÷自由空間伝搬損失
です。送信電力=の式になおすと
送信電力=受信電力×自由空間伝搬損失÷送信アンテナの利得÷受信アンテナの利得
です。したがって、答えは1になります。
A-3 次の記述は、アンテナ特性の可逆性について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) アンテナ特性の可逆性は、アンテナ自体が線形で□A素子のみで構成され、一般に、種々の媒質が同時に存在□B空間で成立する。
(2) 同一アンテナを送信と受信に用いたときの指向性及び利得はそれぞれ等しいが、アンテナ素子がある程度の太さを持ち導体損があるときは、アンテナの□Cは異なる。
| A | B | C |
|---|
| 1 | 能動 | する | 電流分布 |
|---|
| 2 | 受動 | する | 入力インピーダンス |
|---|
| 3 | 受動 | する | 電流分布 |
|---|
| 4 | 能動 | しない | 入力インピーダンス |
|---|
| 5 | 能動 | しない | 電流分布 |
|---|
私は間違えました。AとBは多分、新問です。
まず、Cは覚えてください。アンテナにおいて受信と送信で違うのは電流分布だけです。
Aは「受動」でBは「する」だそうです。ここで私はAの場合「ああ、アンテナが能動だと送信の方に影響を与えて可逆じゃなくなっちゃいそうだから、受動かな」、Bの場合「普通の空間は媒質がたくさんあって、それでも可逆性が成り立つんだな」と覚えます。ホントかどうか知りませんが、こうやってイメージで覚えておくとただ言葉を覚えるよりも頭にのこります。
A-4 図に示す長さが2l[m]の半波長ダイポールアンテナの特性インピーダンスが420[Ω]であるとき、給電点abから見たインピーダンスを純抵抗とするためのアンテナ素子の短縮率として、最も近いものを下の番号から選べ。ただし、位相定数をβ[rad/m]とすれば、長さ2lで特性インピーダンスZ0[Ω]のアンテナのab端子から見たインピーダンスZabは、次式で与えられるものとする。
Zab≒73.1+j42.6−j2Z0cotβl
また、Δが小さな値のとき、次式の関係が成り立つものとする。
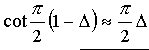
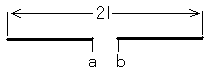
1 1.6[%] 2 2.0[%] 3 2.4[%] 4 3.2[%] 5 4.8[%]
- 短縮率
- 短縮率
短縮率を求める場合は虚数部分(jがついている項)を0にします。
この問題ですと、虚数部分は j42.6−j2Z0cotβl ですので、2Z0cotβlの部分が42.6になるようにします。そうすると、j42.6−j42.6=0になって虚数部分が消えますよね。
- 半波長ダイポールアンテナ
- アンテナの長さが波長の半分であるアンテナのことをいいます。
この問題はcotが出てきていかにも三角関数の知識がないと駄目なように見えますが、知識はいりません。
半波長ダイポールアンテナなので、2l=λ/2です。したがって、l=λ/4です。
βは位相定数です。β=2π/λです。これは決まりです。
Zab≒73.1+j42.6−j2Z0cotβlにlとβを代入すると、Zab≒73.1+j42.6−j2Z0cotπ/2になります。
ところで、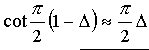 です。ちゃんと考えると、上の式の赤い部分が(π/2)-Δになるんでしょうけど、なってません。それはそれ、cotπ/2の部分を(π/2)Δに置き換えます。
です。ちゃんと考えると、上の式の赤い部分が(π/2)-Δになるんでしょうけど、なってません。それはそれ、cotπ/2の部分を(π/2)Δに置き換えます。
すると、Zab≒73.1+j42.6−j2Z0(π/2)Δ となります。
あとは虚数部分がなくなるように計算するだけですので、
42.6 = 2Z0(π/2)Δ
Z0 = 420[Ω] (と問題に書いてある)ので、これを代入して
Δ = 0.032
答えは3.2%です。
ちなみに位相定数のこととかを知らなくても、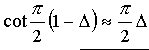 と与えられている時点で「ああ、cotのところを(π/2)Δに置き換えるのね」と考えるのが筋なので、なにも考えなくてもZab≒73.1+j42.6−j2Z0(π/2)Δとします、私は。
と与えられている時点で「ああ、cotのところを(π/2)Δに置き換えるのね」と考えるのが筋なので、なにも考えなくてもZab≒73.1+j42.6−j2Z0(π/2)Δとします、私は。
A-5 次の記述は、特性インピーダンスがZ0[Ω]の給電線と、給電点cdからアンテナ側を見たインピーダンスが純抵抗R[Ω]のアンテナとの整合条件について述べたものである。□内に入れるべき字句の正しい組合せ下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。また、トランスは正結合とする。
(1) 図の等価回路において角周波数をω[rad/s]とし、ab端子間に加わる電圧をV[V]、一次回路及び二次回路の電流をそれぞれI1[A]、I2[A]、一次回路のインピーダンス及び二次回路のインピーダンスをそれぞれZ1[Ω]、Z2[Ω]とすると次式が成り立つ。
V=Z1I1+□A×I2・・・○1
0=Z2I2+□A×I1・・・○2
(2) 一次回路及び二次回路を共に□B状態にすれば、Z1=0、Z2=Rとなるので、○1式及び○2式は、次式となる。ただし、ωL1=1/(ωC1)、ωL2=1/(ωC2)とする。
V=□A×I2・・・○3
0=RI2+□A×I1・・・○4
ゆえに、○3式及び○4式から次式が得られる。
V=□C×I1
(3) ab端子からアンテナ側を見たインピーダンスZ[Ω]は、V/I1で与えられる。整合条件は、一次及び二次回路が□B状態であり、かつ、給電線の特性インピーダンスとZとが等しいことであるから、Z0=□Cとなる。
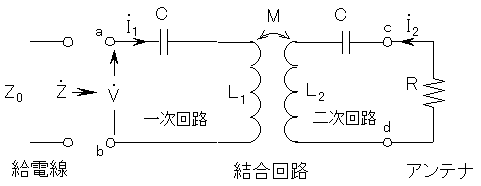 Z0 : 給電線のインピーダンス
Z0 : 給電線のインピーダンス
Z : ab端子からアンテナ側を見たインピーダンス
V : ab端子間の電圧
M : 相互インダクタンス
L1、L2 : 自己インピーダンス
C1、C2 : 静電容量
I1 : 一次回路の電流
I2 : 二次回路の電流
| A | B | C |
|---|
| 1 | jωM | 平衡 | ωM/R |
|---|
| 2 | jωM | 共振 | (ωM)2/R |
|---|
| 3 | jω(L1+L2) | 共振 | ω(L1+L2)/R |
|---|
| 4 | jω(L1+L2) | 共振 | ω2(L1+L2)2/R |
|---|
| 5 | jω(L1+L2) | 平衡 | ω2(L1+L2)2/R |
|---|
多分新問ですが多少の知識があれば大丈夫です。
まず□Bですが、「平衡」という言葉は試験に出ないです。また回路の状態を指す言葉は「共振」だけしか出ません。
次に□Aですが、インピーダンスがjω(L1+L2)になる回路を書いてみましょう。下の図のようになることは容易に分かります。当たり前ですよね。
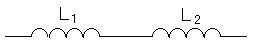
そんなわけで、□AはjωMです。よって答えは2です。
ちなみにこの問題は、解答の選択肢と回路図を見るだけで1と分かります。まず「共振」を選んで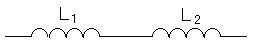 という回路が存在しませんので。
という回路が存在しませんので。
・・・詳しい解説いります?
A-6 特性インピーダンスが70[Ω]の同軸給電線において外部導体の内径が内部導体の外径の10倍であるとき、内部導体と外部導体の間に用いられている誘電体の誘電比率の値として、最も近いものを下の番号から選べ。
1 3.9 2 6.5 3 7.8 4 13.2 5 15.6
ぱっと選択肢を見たとき、誘電率が13とか15とかの物体ってあるんかなあ・・・普通3くらいだよなあ・・・なんて思います。と思ったら、過去問の解説によると比誘電率10程度のものを使っているそうで・・・
知らないと解けない問題ですが、結構出るので公式を覚えてください。
同軸線路の特性インピーダンス


Z0[Ω](特性インピーダンス) D[m](外部導体の内径) d[m](内部導体の外径) εr(比誘電率)
Z0=138/ε1/2logD/d
外部導体の内径が内部導体の外径の10倍なので、D/dは10です。log10=1ですので、logD/d=1です。したがって
70=138/ε1/2
ε1/2≒2
ε≒4
よって答えは1です。
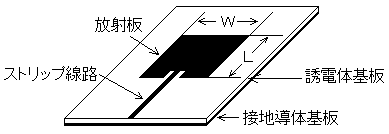
A-7 次の記述は図に示すマイクロストリップ線路について述べたものである。このうち誤っているものを下の番号から選べ。
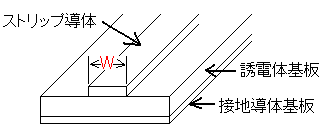
1 誘電体基板には、比誘電率の小さい誘電体を用いている。
2 特性インピーダンスは、幅Wが狭いほど高くなる。
3 TEMモードに非常に近いモードが伝送される。
4 一種の開放線路であるので外部雑音が混入する恐れがある。
5 TEMモードによって伝送可能な最高周波数は、同軸線路に比べて高くできる。
あまり知識がなくても分かるでしょう。
まず、1を読んだ瞬間に1が答えだと分かります。比誘電率は大きい方がいいです。覚えてください。比誘電率が1ということは誘電体じゃない(つまり空気を使用する)ということですが、比誘電率が小さい誘電体を用いるということは極端に言うと比誘電率が1の誘電体を使用した方がいいということになって、それじゃ誘電体なんていらないということになってしまいます。ここで矛盾が生じます。
2は、幅が狭いということは、断面積が小さくなるってことで、電気が流れるパイプが小さくなるので特性インピーダンスは高くなるにきまっています。
3の事実は、覚えておいて損はないです。覚えましょう。
4は過去にも出ました。まあ、導体がむき出しだから雑音が進入して当然と覚えればOKでしょう。
5はそういうことらしいです。確かにマイクロ波帯域ではマイクロストリップ線路が用いられます。同軸ケーブルにマイクロ波を通すと減衰が激しいです。
まず、導波管は長い方と記憶します。そして、位相速度と群速度では群速度(エネルギーの伝わる速度)の方が遅いです。これは覚えてください。
まず、Dは群速度の方が遅いので「遅い」です。一陸特の基本です。一陸技ではあんまり出なかった記憶がありますが。
次に、Bですが「導波管は長い方」で、aとbではaの方が長いので2aの方を選びます。ですから、Bは2aです。
Cも同様に「導波管は長い方」なので、aとbではaの方が長いのでaが入っている方を選びます。したがって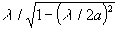 を選びます。
を選びます。
解答は4です。
ところで、遮断波長が2aというのも一陸特の常識ですので、覚えておかないと駄目でしょう。
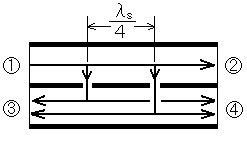
A-9 図に示す理想的な2結合孔方向結合器において、端子○1から電力P1[W]を入力とし、端子○2、○3及び○4にそれぞれ電力P2[W]、P3[W]及びP4[W]が出力されたときの結合度Cを表す式として、正しいものを下の番号から選べ。ただし、線路○1−○2は主伝送路、○3−○4は副伝送路で、管内波長をλg[m]とする。
1 C=10log10P2/P1[dB]
2 C=10log10P3/P1[dB]
3 C=10log10P4/P1[dB]
4 C=10log10P3/P2[dB]
5 C=10log10P4/P2[dB]
まずこういう問題で基準となる電力は絶対にP1[W]です。絶対に入力が基準になります。したがって、4と5は候補から外れます。
次に、結合度を知りたいってことは、結合している方のパラメータが入っていないと駄目ですので、1も候補から外れます。○1から○2を結合度と言いそうにないですよね。したがって、解答の候補は2か3です。あとは運です。
ちなみに、工担もそうなのですがだいたい知りたいのは、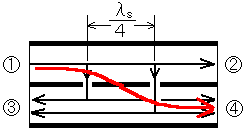 の赤い線を通った場合の損失?です。したがって、答えは3です。
の赤い線を通った場合の損失?です。したがって、答えは3です。
A-10 次の記述は放送用アンテナについて述べたものである。このうち誤っているものを下の番号から選べ。
1 電気長が約0.54波長の垂直接地アンテナは、中波放送のフェージング軽減用として用いられる。
2 ビームアンテナ(カーテンアンテナ)は、短波放送で遠距離の特定地域に向けて送信する場合に用いられている。
3 スーパターンスタイルアンテナは半波長ダイポールアンテナ2個を直交させて支持柱に取り付けたものであり、主にVHF帯テレビジョン放送用として用いられている。
4 スーパゲインアンテナは、反射板付きダイポールアンテナを鉄塔の各面に取り付けたものであり、主にFM放送及びVHF帯テレビジョン放送用として用いられる。
5 双ループアンテナは、周の長さが約1波長のループアンテナ2個を一定間隔離して給電線で結び、反射板と組み合わせたものを基本構成とし、これを鉄塔の各面に取り付けたものであり、FM放送からUHF帯のテレビジョン放送まで広く用いられている。
間違えました。
答えは3です。半波長ダイポールアンテナではなく、バッドウィングアンテナを直交させるそうです。スーパターンスタイルアンテナを見ると

となっていますが、このアンテナの給電線の形が羽みたいになってますよね。これがバッドウィングのようです。とりあえず、私はスーパターンスタイルアンテナのイメージを頭に焼き付けて「羽」というキーワードだけ覚えます。
ちなみに、この問題の文章は誤っているものを除いてすべて暗記すべきです。
A-11 次の記述はカセグレンアンテナについて述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) 回転放物面の主反射鏡、回転双曲面の副反射鏡及び一次放射器から構成され、副反射鏡の二つの焦点の一方は主反射鏡の□Aと、また、他方は一次放射器の励振点と一致させてある。
(2) 主反射鏡及び副反射鏡双方の鏡面を本来の曲面からわずかに変える□Bが可能であり、これにより高能率で低雑音の特性が得られる。
(3) 一次放射器を主反射鏡の中心近くに置くことができるため、□Cを短くできる。
| A | B | C |
|---|
| 1 | 開口面 | 鏡面修正 | 焦点距離 |
|---|
| 2 | 開口面 | モード変換 | 焦点距離 |
|---|
| 3 | 焦点 | モード変換 | 給電回路 |
|---|
| 4 | 焦点 | モード変換 | 焦点距離 |
|---|
| 5 | 焦点 | 鏡面修正 | 給電回路 |
|---|
問題を作った方がは苦しかっただろうと思われる問題です。少しの知識があれば解けます。確か過去問にこれと同じような問題が出ています。その時も、何考えて作ったんだろうと思いましたが。
まず、□Bです。「鏡面を本来の曲面からわずかに変える」のですから「鏡面修正」でしょう。モード変換はどう考えても入りそうにないです。
次に、□A。「一致させてある」とありますが、一致する可能性があるのは「焦点」でしょう。開口面は一致するには広すぎます。だって、面ですから。面に一致出来るのは面だけで、点は面に一致するって言いませんよね。
さらに□C。焦点距離と給電回路、短くてうれしいのは給電回路です。焦点距離を短くしても何も変わらないです。
したがって答えは5です。
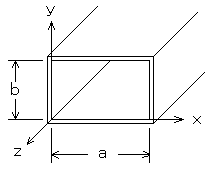
A-12 開口面の縦及び横の長さがそれそれ15[cm]及び25[cm]の角錐ホーンアンテナを、周波数2[GHz]で使用したときの利得(真値)として、最も近いものを下の番号から選べ。ただし、電界(E)面及び(H)面の開口効率を、それそれ0.75及び0.8とする。
1 1.9
2 4.2
3 8.4
4 10.3
5 12.6
知らなきゃ解けませんがよく出るので知っているべきでしょう。「電界(E)面及び(H)面の開口効率」が出ているあたりが新問です。
アンテナの実効面積などなど(重要)

Ae[m2](アンテナの実効面積) A [m2](アンテナの面積) λ [m](波長) G [単位なし](利得) η[単位なし](開口効率)
まず資格試験の基本は「出ている数字は全部使う」です。だいたい無駄な数字はないです。次に「効率」はかけ算するしか使い道がないです。効率が出てきたらかけ算しましょう(真数の場合です)。
上の公式より
G=4πηA/λ2
まず、Aですが開口面の縦及び横の長さがそれそれ15[cm]及び25[cm]なので、A=0.15×0.25=0.0375
ηは開口効率が2つ(0.75及び0.8)があるので、とりあえずかけ算します。η=0.75×0.8=0.6
波長はλ=3.0×108/周波数=3.0×108/2×109=1.5×10-1=0.15
よって
G
=4πηA/λ2
=4×3.14×0.6×0.0375/0.152
=12.56
答えは5です。
ちなみに、私は最初「効率はどっちかしか使わないんじゃないか」と思って計算したのですが、そうすると選択肢の中で一番大きい数字より大きくなってしまうので、どっちも使わないと駄目かという結論に達しました。
まず□Bです。εs=1のとき半波長ダイポールアンテナが共振する長さで、半波長ダイポールアンテナが共振する長さはλ/2です。したがって、解答は2か4です。後は運です。
運なのですが、なんとなく影像だと思いました。導波器は図に載っていないので多分却下だと思いました。で、影像っていうのは、なんて言ったらいいかわからないので、参考書の接地アンテナの説明を見てください。簡単に図で描くと以下のようになります。
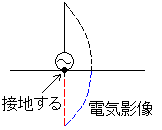
接地アンテナは、地面が鏡みたいになって地上にあるアンテナと同じように地面の下にもアンテナが出来ます(これが赤い線です)。地面の下にもアンテナがあるので、当然そこに電気が流れていると考えてよいです。それが青い線です。この青い線のことを多分電気影像といます。
要するに接地アンテナには電気影像が出来るということです。
A-14 次の記述は、短波通信で使用されるMUF(最高使用周波数)及びFOT(最適使用周波数)について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) 毎日の同じ時刻におけるMUFの値は、多くの原因により変動しているので、予報することが困難である。そのため、MUFの予報値は、対象とする月のMUFの1ヶ月間の□Aとして予報される。したがって、MUFの予報値を使用周波数とした場合、同じ時刻の1ヶ月間で通信が可能な日数の割合は□Bとなることが考えられる。
(2) 通信が可能な日数の割合は、MUFに近い周波数では周波数が低いほど大きくなり、MUFの予報値の□C倍の周波数において90%となる。この周波数をFOTという。
| A | B | C |
|---|
| 1 | 最大値 | 10パーセント | 0.85 |
|---|
| 2 | 中央値 | 50パーセント | 0.85 |
|---|
| 3 | 最小値 | 50パーセント | 0.76 |
|---|
| 4 | 中央値 | 10パーセント | 0.76 |
|---|
| 5 | 最大値 | 10パーセント | 0.76 |
|---|
みなさんは平均値と中央値と最頻値の違いが分かりますか? この問題は無線の問題ではなく統計の知識があるかないかのです(半分本当
□Aと□Bの組合せをみます。「最大値」として予報されたとき、その周波数を使うと「通信が可能な日数の割合は10パーセント」になる、というのははっきり言ってよくわからないです。何を根拠に10パーセントだかさっぱりわからないです。最高値を取るのは多分月に1回でしょうから(だって、最高値ですよ、どの程度の精度で予報を出すのか知りませんが、1Hzの精度で予報を出したら、最高使用周波数がぴったり一致する日なんて存在しないので、最高値をとる日も1日しかないはず)確率で言えば1/30で4%ほどといったところでしょうか。一方「中央値」を使用周波数にすると、本日の最高周波数が予報された値(中央値)を超えてしまう確率が50%、中央値を下回る可能性が50%ですので、通信が可能なのは中央値より周波数が低い場合なので50%です。したがって、中央値と50パーセントの組合せが正しいです。答えは2です。
ちなみに、最高周波数×0.85=最適周波数は無線屋の常識として覚えておきましょう。ときどき試験に出ます。
A-15 次の記述は、ラジオダクトの成因について述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) 昼間、太陽に熱せられた大地が、日没とともに熱を放射して冷却する。この熱は、乱流によって大気の下層部に供給され、温度の逆転層を生じ、□Aダクトを生ずる。このようなダクトを夜間冷却によるダクトという。
(2) 高気圧圏では下降気流があり、この下降気流は乾燥しているため、蒸発の盛んな大地又は水面の近くに下降すると、□Bの逆転層を生じ、S形ダクトを生ずる。このようなダクトを沈降によるダクトという。
(3) 昼間、海上で生じた接地形ダクトが海風によって海岸地帯まで運ばれる。このようなダクトを□Cによるダクトという。
| A | B | C |
|---|
| 1 | 接地型 | 温度 | 移流 |
|---|
| 2 | S形 | 温度 | 海風 |
|---|
| 3 | 接地型 | 湿度 | 移流 |
|---|
| 4 | S形 | 湿度 | 陸風 |
|---|
| 5 | 接地型 | 温度 | 海風 |
|---|
何も知らなくてもわかります。
まず、Bでは「乾燥」とか「蒸発」とか言葉が出てきます。温度と湿度、どちらを選ぶかといえば湿度でしょう。
次に、Aです。(2)でS形ダクトの話をしているので、(1)で「S形」を選ぶのは不適当です。これは、そういうもんです。普通、その問題文中に答えは存在しないものです。
よって答えは、3です。ちなみに「移流」という言葉は覚えて置いて損はないです。意味は知らなくていいので、「移流」という言葉を頭にとどめておきましょう。このおかげで私は□Cを見たときに「移流」は見たことがあるけど「海風」というのは見たことがないと思って「移流」を選びました。
A-16 次の記述は、中緯度地方のスポラジックE層について述べたものであるこのうち誤っているものを下の番号から選べ。
(1) 高度が約100〜150キロメートル前後に現れる層の厚さが極めて薄い電離層である。
(2) 最大密度は、F層の最大電子密度を超えることがある。
(3) 冬季より夏期の方が、また、夜間より昼間の方が出現頻度は高い。
(4) 太陽活動が活発になると、その出現頻度及び最大電子密度は高くなる。
(5) 出現時刻が不規則であり、また、最大電子密度は不安定である。
間違えました。一アマとして悲しいです。答えは、4です。スポラジックE層だけが太陽の影響を受けないです。F層は太陽の影響を受けます。D層とE層は、F層ほどではないですが影響を受けます。
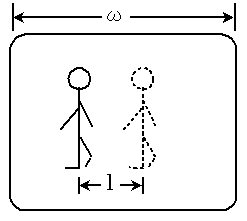
A-17 図は、テレビジョン受信機の画面に現れた1回反射波のゴースト(多重像)の一例である。画面上の水平走査ωが50[cm]、画面上の真の画像とゴーストの間隔lが15[cm]のとき、ゴーストを起こしている反射波と直接波の伝搬距離差の差の値として、正しいものを下の番号から選べ。ただし、画面の左端から右端までを操作する時間は8×10-5[秒]とする
 1 360[m]
2 720[m]
3 2.4[km]
4 3.6[km]
5 7.2[km]
1 360[m]
2 720[m]
3 2.4[km]
4 3.6[km]
5 7.2[km]
とりあえず、何もわからなくても選択肢の3は選びません。無線の試験はだいたい桁が違うものが2組用意されています。この問題ですと、1と4、2と5の組です。仲間はずれの3は解答ではないです。
ωが50[cm]で、ωだけ走査するのに8×10-5[秒]かかるので、lの15[cm]は何秒かというと、
50[cm] : 8×10-5[秒] = 15[cm] : x
x = 2.4×10-5[秒]
です。ということは、反射波が直接波に比べて2.4×10-5[秒]遅れてきてるってことです。電波は1秒間に3.0×108[m]進むので、
2.4×10-5[秒]×3.0×108[m/秒]=7200[m]
よって、答えは5です。ちなみに、3.0×108[m/秒]をかけ算することが分からなくても、2.4×10-5[秒]が出たところで、選択肢の3は解答から外れます。なぜなら、この2.4という数字が出たときに試験を受けている人が勘違いして、3と5を選んでしまうために作った選択肢と思われるからです。
よく出る問題ですので丸暗記するべきでしょう。解答の正しい選択肢を。式の展開などはする必要はありません。
まず□Aですが、「パラボナアンテナ」と「距離」というキーワードが出たら「位相差」しかないです。「ひずみ」は無線工学Bには出てきません。ひずみはアンプの非直線性増幅にしか出てきません。したがって□Aは位相差です。
次に□Bの近似の問題ですが、よく出ますので覚えて下さい。大学の数学の常識です。つまり一般世界の非常識ってことですが。
α<<1の時 (1+α)n ≒ 1+nα
要するにかっこの外の次数が前に出ればいいということです。今回は上の式のnにあたる数字が1/2なので、1/2が前に出てればいいということです。したがって、□Bは選択肢の2か4になります。
□Cは□Bが出来ていれば自動的にできますね。
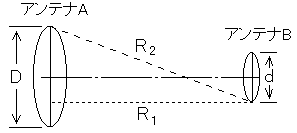
□Dは□Cと連動しているので□Cが出来ればいいのですが、よく出るので覚えてください。両アンテナ間の最小距離Rmin[m]は係数が2と。これと類似の問題は私の記憶が確かならば係数か次数が違う問題しかでていません。多分、これからもそうでしょう。ですから、式の細かいところはいいので係数だけは暗記してください。2です。
A-19 長さl[m]の無損失給電線り終端を開放及び短絡して入力端から見たインピーダンスを測定したところ、それぞれ-j40[Ω]及び+j90[Ω]であった。この給電線の特性インピーダンスの値として、正しいものを下の番号から選べ。
1 60[Ω]
2 75[Ω]
3 90[Ω]
4 130[Ω]
5 150[Ω]
インピーダンスが2つ出てきたら、かけ算してルートをとったものがだいたい答えです。ごくまれに違うのがありますけど、かけ算してルートをとっておけば当たることが多いです。
よって
(−j40×j90)1/2
=60[Ω]
答えは1です。
A-20 次の記述は、近傍界におけるアンテナ特性の測定について述べたものである。このうち誤っているものを下の番号から選べ。
1 自由空間に近い環境が得られる電波無響室(電波暗室)のクワイエットゾーン内に被測定アンテナを置いて測定する。
2 アンテナの近傍界の測定値を用いて、計算により遠方界におけるアンテナ特性を推定する。
3 被測定アンテナの放射近傍領域内で測定用プローブを移動して測定する。
4 測定用プローブとして、主に八木アンテナあるいはホーンレフレクタアンテナが用いられる。
5 測定用プローブを移動する(スキャン)方法には、被測定アンテナの前方平面上を移動させる平面走査法、被測定アンテナを中心にした垂直円筒上を移動させる円筒走査法及び球面上を移動させる球面走査法などがある。
少なくとも3は選んではいけません。5で測定用プローブを移動すると書いてあって、3でも移動すると書いてあります。3の内容は5の内容に含まれることが書いてあるので3は選んではいけません。でも、5はもしかしたら平面走査法とかの名前が違うかもしれないので5が誤っているとは言い切れません。あとは運です。
運なのですが、2は過去問に出ています。近傍界から遠方界を計算で出せます。したがって、2は選んではいけません。
答えは4で八木アンテナは使わないで、半波長ダイポールアンテナを使うそうです。私はこの問題間違えました。
まず選択肢のグループ分けです。1と4、2と5、3と7、6と8、9と10に分けられます。
□アは「入力」か「放射」が入ります。この問題の話題はアンテナから放射される電波を問題にしているので「放射」です。
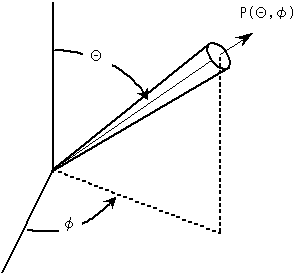
□イは6か8があてはまります。□イの単位は無次元でP(θ,φ)maxの単位は[W/rad2]と問題に書いてあるので、答えの分子の単位も[W/rad2]でないと駄目です。PtとPaでは、Paの単位が[W/rad2]ですので、答えは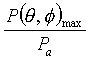 です。
です。
□ウは2か5があてはまります。立体角が2πなのか4πなのかということですが、2πが立体角というのは聞いたことがないし、2πといったら普通円の面積とか円周の長さに使って、4πといったら球の表面積とか球の体積で使うのでいかにも立体という感じです。したがって答えは4πです。
□エは1か4が入ります。□エの前の文章を読むと、「全放射電力が集中していることになり」とあるので利得は高くなるに決まってます。したがって答えは「大きく」です。
□オは9か10が入ります。これは運です。運なのですが、ちょっと考えると、□ウで2πを選んだ時にまともに計算すると□オがの解答が10になって□ウで4πを選んだ時に□オの解答が9になるんじゃないかと考えます。したがって、ここは9を選ぶべきです。
ア:3 イ:8 ウ:2 エ:4 オ:9
B-2 次の記述は、図に示すハイブリッドリング回路について述べたものである。□内に入れるべき字句を下の番号から選べ。
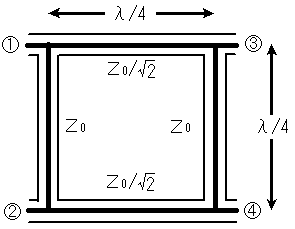 ただし、図において、端子○1−○2間と端子○3−○4間及び端子○1−○3間と端子○2−○4間の同軸給電線の特性インピーダンスは、それぞれZ0[Ω]及びZ0/21/2[Ω]であり、回路を構成する給電線の長さはすべて1/4波長とし、波長をλ[m]とする。
ただし、図において、端子○1−○2間と端子○3−○4間及び端子○1−○3間と端子○2−○4間の同軸給電線の特性インピーダンスは、それぞれZ0[Ω]及びZ0/21/2[Ω]であり、回路を構成する給電線の長さはすべて1/4波長とし、波長をλ[m]とする。
(1) 端子○3及び○4にそれぞれZ0[Ω]のインピーダンスを接続し、端子○1に入力電力を加えれば、端子○3及び○4には□ア度位相が異なり、入力電圧の□イ倍の出力電圧が現れるが、端子○2には現れない。
(2) 端子○2にZ0のインピーダンスを接続し、端子○3及び○4にそれぞれ相等しい□ウを接続すると、端子○1に加えた入力電圧はすべて□エに出力される。
(3) 端子○3及び○4にそれぞれZ0[Ω]のインピーダンスを接続し、端子○1及び○2に大きさが等しい電圧を加えたとき、端子○1の電圧の位相が端子○2の位相より90度□オいれば端子○3に、また、逆の場合には端子○4に出力される。
1 遅れて
2 1/21/2
3 21/2
4 端子○4
5 端子○2
6 進んで
7 純リアクタンス
8 180
9 90
10 純抵抗
まず選択肢のグループ分けです。1と6、2と3、4と5、7と10、8と9です。
□アは180か90が入ります。端子○1から見て端子○3と端子○4は距離がλ/4だけ違います。したがって端子○3と端子○4では位相は90度ずれます。□アは90です。
□イは1/21/2か21/2ですが、例えば○1から1の電力を入力して○3に21/2の電力が出力されたら電力が増えてることになり、それはおかしいので答えは1/21/2です。
次に□ウと□エです。□エには端子○4か端子○2が入ります。「端子○3及び○4にそれぞれ相等しい□ウを接続すると、端子○1に加えた入力電圧はすべて□エに出力される」のですから、端子○3、端子○4は同じ条件なのでもし端子○4に出力されるのだったら端子○3にも出力されるはずです。したがって端子○4にだけ出力されるというのはおかしいので、□エは端子○2になります。
□ウは純リアクタンスか純抵抗が入ります。端子○1に入った電力が端子○2だけに出力されるので端子○3、端子○4には電力が流れてはいけないということになります。電波は交流で交流を阻止できるのは純リアクタンスです。したがって、□ウは純リアクタンスです。
□オは考えるのが面倒なので運にまかせてもいいと思いますが、考えれば分かります。
端子○2に端子○1より位相が90度遅れた電圧を加えたとすると、イメージは下の図のようになります。
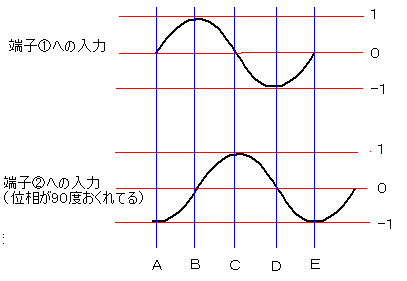
端子○1に入った電圧が端子○3に到達するまでにはλ/4の距離があるので、端子○1から入った電圧より位相が90度遅れたものが端子○3における出力になります。図で表すと下のような波形になります。
端子○2に入った電圧が端子○3に到達するまでにはλ/2の距離があるので、端子○2から入った電圧より位相が180度遅れたものが端子○3における出力になります。図で表すと下のような波形になります。
上の2つの図をじっとみると、位相がちょうど180度違っていることに気づきます。したがって端子○2に端子○1より位相が90度遅れている電圧を加えると、つまり端子○1の電圧が端子○2の電圧の位相より90度進んでいれば端子○3の出力は0になります。
ということは、「遅れていれば端子○3に出力される」んじゃないかなーと考えます。
ア:9 イ:2 ウ:7 エ:5 オ:1
B-3 次の記述は、計器着陸装置(ILS)用アンテナについて述べたものである。□内に入れるべき字句を下の番号から選べ。ただし、□内の同じ記号は、同じ字句を示す。
ILSは、航空機を電波で誘導し、安全に滑走路へ着陸させるための装置であり、グライドパス、ローカライザ及びマーカービーコンから構成されている。
(1) グライドパス用のアンテナは、ヌルリファレンス形の場合、直接波と大地反射波の合成波を利用するために2個又は3個の□アアンテナを垂直方向に配列したものであり、滑走路の延長線上で進入端より300メートル、滑走路の横方向に120〜150メートルそれぞれ離れた地点に設置されている。□アアンテナからの直接波と大地反射波との合成で作られる複数のローブから進入に適した二つを選び、その二つのローブのヌル点方向を航空機の□イ方向の進入コースとして与える。
(2) ローカライザ用のアンテナは、複数個のコーナレフレクタアンテナや対数周期アンテナなどを□ウしたものであり、滑走路の延長線上で滑走路端から約200メートルの地点に設置されている。放射パターンは、航空機の進入方向に対して対称で大きさの等しい二つの□エを持ち、□イ方向に直交する方向の進入パターンを与える。
(3) マーカ用のアンテナは、滑走路進入方向の延長線上で進入端から決められた距離に、インナマーカ、ミドルマーカ及びアウタマーカとして、2素子の半波長ダイポールアンテナを垂直に立てたものである。放射パターンは、□オビームであり、アンテナ上空を通過し滑走路へ進入する航空機に対して滑走路進入端からの距離を与える。
1 パラボラ
2 ファン
3 縦に配列
4 ローブ
5 ペンシル
6 横に配列
7 上下
8 左右
9 コーナレフレクタ
10 ヌル点
勘弁してください級の新問です。
とりあえず、選択肢のグループわけです。1と9、3と6、7と8は分かるのですが、2と4と5と10はよくわからないので保留します。
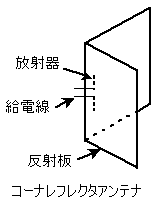 □アですが、パラボラアンテナかコーナレフレクタアンテナです。パラボラアンテナを垂直に配置するというのは考えにくいですし、パラボラアンテナは指向性がするどくて大地反射波を利用するようなアンテナじゃないし、確か大地反射波を嫌うアンテナという認識が私の中にあったので、コーナレフレクタアンテナです。
□アですが、パラボラアンテナかコーナレフレクタアンテナです。パラボラアンテナを垂直に配置するというのは考えにくいですし、パラボラアンテナは指向性がするどくて大地反射波を利用するようなアンテナじゃないし、確か大地反射波を嫌うアンテナという認識が私の中にあったので、コーナレフレクタアンテナです。
ちなみに、吉川忠久『1・2陸技受験教室○3』東京電機大学出版 2000 によるとコーナレフレクタアンテナはVHF、UHF帯の固定通信用や無線呼び出しなどの基地局アンテナ、計器着陸装置(ILS)のグライドパス用アンテナなどに用いられているそうです。
次に□イです。答えとしては上下と左右が考えられます。問題文に「直接波と大地反射波の合成波を利用する」とあります。直接波と大地反射波から分かりそうなのは上下の位置な気がします。したがって□イは上下です。
□ウですが、グライドパスではアンテナを垂直に配置して上下の位置関係を取得していると思われました。ということは、ローカライザの方は横方向かなあとなんとなく思います。したがって、アンテナは横に配列しそうです。したがって□ウは横に配列です。
□エは放射パターンの話をしています。放射パターンに関する用語で2と4と5と10から選べるのは「ローブ」くらいです(放射パターンとか指向性の話のところで「サイドローブ」という言葉が出てきますよね)。したがって□エはローブです。
□オは・・・運です。私は間違えました。ファンだそうです。
ア:9 イ:7 ウ:6 エ:4 オ:2
B-4 次の記述は、図に示すナイフエッジの形をした山頂の点Cにおける回折損を誘導する過程について述べたものである。□内に入れるべき字句を下の番号から選べ。ただし、□内の同じ記号は同じ字句を示す。また、大地の反射係数は-1とし、距離d1[m]及びd2[m]は、高さh0、h1及びh2に比べて十分大きいものとする。
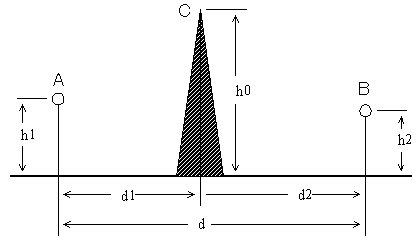 (1) 送受信点間にナイフエッジが無い場合、自由空間の電界強度をE0[V/m]とすれば、B点における地上波電界強度Edは、次式で与えられる。
(1) 送受信点間にナイフエッジが無い場合、自由空間の電界強度をE0[V/m]とすれば、B点における地上波電界強度Edは、次式で与えられる。
Ed=□ア×sin(2πh1h2/λd)[V/m] …○1
(2) ナイフエッジがある場合の回折損をSとすれば、B点における電界強度Eは、次式となる。
Ed=□イ×sin(2πh1h0/λd1)×sin□ウ[V/m] …○2
(3) h1を上下に変化させてEが最大になったときには、次式となり、
sin(2πh1h0/λd1)=□エ …○3
h2を変化させてEが最大になったときには、次式となる。
sin(ウ)=□エ …○4
(4) したがって、○2、○3及び○4式より、回折損Sは次式で示される。
S=□オ
1 2E0 2 4E0S 3 sin(2πh2h0/λd2) 4 E0 5 E0S
6 1 7 E/4E0 8 sin(2πh1h2/λd2) 9 E/E0 10 1/2
- 直接波と大地反射波の合成電界
- 直接波と大地反射波の合成電界
まず解答のグループわけです。
1と4、2と5、3と8、6と10、7と9が対です。
□アですが、知らなきゃ分かりません。また、ここで間違えると後の選択肢の大部分を間違えます。答えは1です。この式は暗記してください。
□イですが、「回折損をSとすれば」なのでSが入っているものを選びます。単純に考えると、□アで4を選んだ方用に5の解答を作って、□アで1を選んだ方用に2の解答を作っている気がします。したがって、2を選びます。こんな説明で納得いくか、と思う方は自分で勉強してくださいと言いたいところですが、簡単なので説明します。
まず、下の図の黒丸の所の合成受信電界強度を求めます。
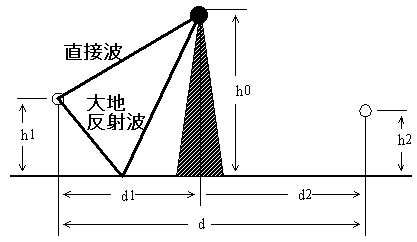
送信アンテナの高さがh1[m]、黒丸の高さがh0[m]、距離はd1[m]なので黒丸の点の電界強度は2E0×sin(2πh1h0/λd1)[V/m]。
次に黒丸のところから、受信アンテナのところまで電波が飛びます。黒丸のところから出る電波の強度は2E0×sin(2πh1h0/λd1)[V/m]に回折損Sをかけて、2E0S×sin(2πh1h0/λd1)[V/m]になります。これをE0'としましょう。
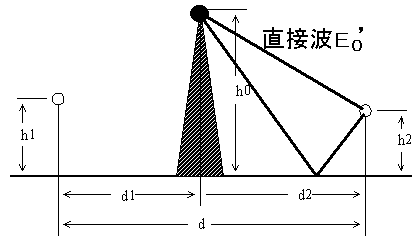
黒丸の高さがh0[m]、受信アンテナの高さがh2[m]、距離はd2[m]なので受信アンテナの電界強度は2E0'×sin(2πh0h2/λd2)[V/m]。ここで、E0'=2E0S×sin(2πh1h0/λd1)なので、受信アンテナの電界強度は4E0S×sin(2πh1h0/λd1)×sin(2πh0h2/λd2)
□ウですが、上に答え書いてしまったんですけど、Ed=□イ×sin(2πh1h0/λd)×sin□ウ[V/m]で、最初のsinの項はh1からh0のことを指しているので、□ウはh0からh2のことを指さないといけないです。したがって答えは3です。
やっと□エです。三角関数を使うのはこれだけです。h1を上下に変化させるということはsinの値が上下するってことです、sinの値は1〜-1の値をとります。sinが1をとった時にEが最大になります(よね、-1より1の方が大きいですよね)。したがって、□エは6です。
□オですが、○2の式でsinの値が1の時はE=4E0Sになります。したがって、S = E / 4E0です、答えは7です。
ア:1 イ:2 ウ:3 エ:6 オ:7
B-5 次の記述は、電波無響室(電波暗室)に使用する電波吸収体及びその特性について述べたものである。このうち正しいものを1、誤っているものを2として解答せよ。
ア 使用する材料には導電性材料、誘電性材料及び磁性材料がある。
イ ある周波数以上で使用できる広帯域形と、ある周波数帯内だけで使用できる狭帯域形がある。
ウ 広帯域形の場合、周波数が低くなれば吸収体の厚さを薄くする必要がある。
エ 広帯域形は、使用波長に対する吸収体の厚さの比が大きいほどよい。
オ 電波がいかなる偏波及び角度で入射しても、吸収がよいことが望ましい。
電波暗室に関する問題はよく出る気がします。どっかに電波暗室に関する資料はないですかねえ。
何も知らなくても分かるのは、オです。
オですが、常識的に考えて「電波無響」なのですから、あるゆる周端数が無響な方がうれしそうです。したがってオは○です。
あとは運です。
運ですが、アは知っていれば○とすぐに分かります。
イは○でウは×でエは○だそうです。
ア:1 イ:1 ウ:2 エ:2 オ:1
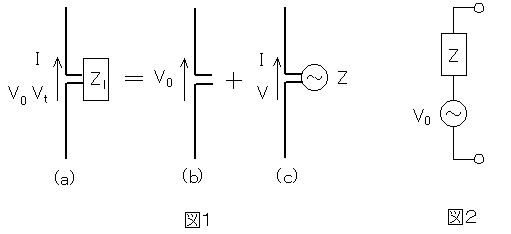

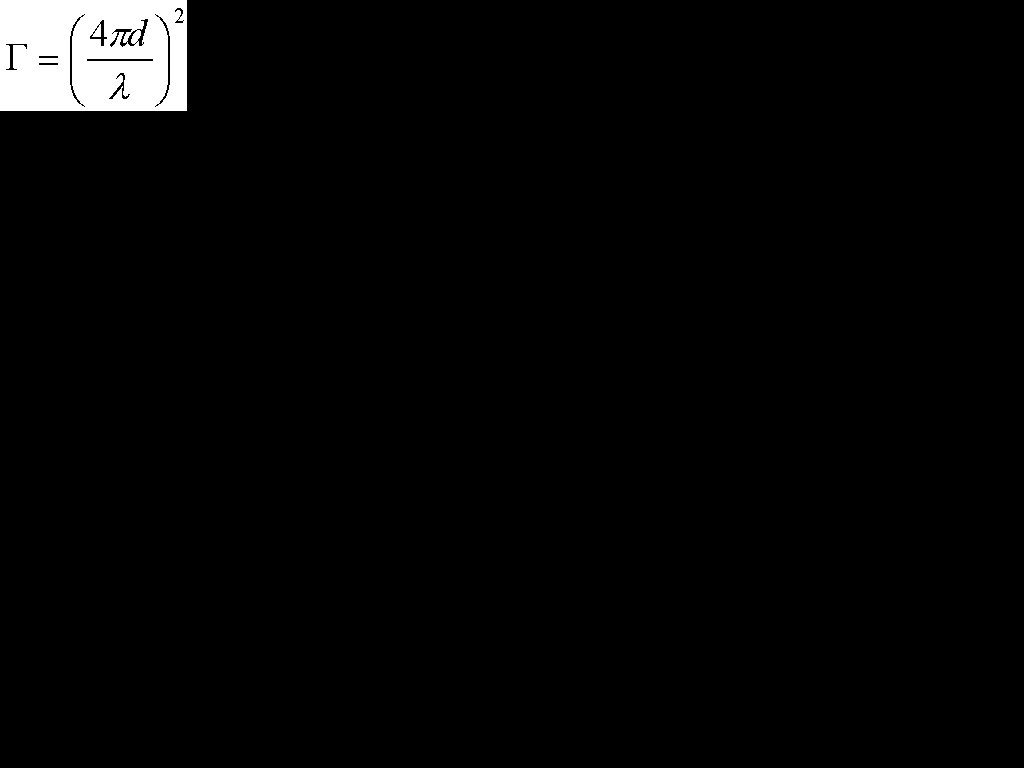
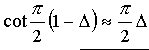
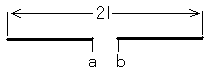
 Z0 : 給電線のインピーダンス
Z0 : 給電線のインピーダンス



 の赤い線を通った場合の損失?です。したがって、答えは3です。
の赤い線を通った場合の損失?です。したがって、答えは3です。




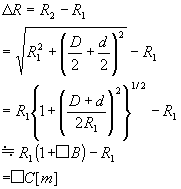
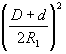
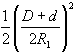
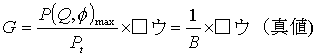 ・・・ [2]
・・・ [2]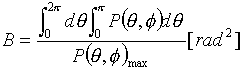
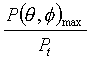
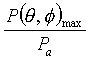
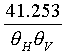
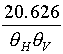
 ただし、図において、端子○1−○2間と端子○3−○4間及び端子○1−○3間と端子○2−○4間の同軸給電線の特性インピーダンスは、それぞれZ0[Ω]及びZ0/21/2[Ω]であり、回路を構成する給電線の長さはすべて1/4波長とし、波長をλ[m]とする。
ただし、図において、端子○1−○2間と端子○3−○4間及び端子○1−○3間と端子○2−○4間の同軸給電線の特性インピーダンスは、それぞれZ0[Ω]及びZ0/21/2[Ω]であり、回路を構成する給電線の長さはすべて1/4波長とし、波長をλ[m]とする。


 □アですが、パラボラアンテナかコーナレフレクタアンテナです。パラボラアンテナを垂直に配置するというのは考えにくいですし、パラボラアンテナは指向性がするどくて大地反射波を利用するようなアンテナじゃないし、確か大地反射波を嫌うアンテナという認識が私の中にあったので、コーナレフレクタアンテナです。
□アですが、パラボラアンテナかコーナレフレクタアンテナです。パラボラアンテナを垂直に配置するというのは考えにくいですし、パラボラアンテナは指向性がするどくて大地反射波を利用するようなアンテナじゃないし、確か大地反射波を嫌うアンテナという認識が私の中にあったので、コーナレフレクタアンテナです。 (1) 送受信点間にナイフエッジが無い場合、自由空間の電界強度をE0[V/m]とすれば、B点における地上波電界強度Edは、次式で与えられる。
(1) 送受信点間にナイフエッジが無い場合、自由空間の電界強度をE0[V/m]とすれば、B点における地上波電界強度Edは、次式で与えられる。
