一陸技

修正

　A-10を利根のカッパさんの情報により書き足しました。利根のカッパさんありがとうございました。

平成12年1月

　さて、私はこの問題を読んだとき、さっぱり意味が分かりませんでした（爆　フラウンフォーファ領域？？？、フルネル領域？？？という感じです。が、作ったのは所詮人間解決の糸口はあります。
　まず1.を読むと、放射角度に対する電界パターンが距離によってほとんど変化しないとありますので「ああ、なるほどフラウンフォーファ領域ってのは遠くの方だな」と思います（思えない方へ、電波ってのはアンテナに近いといろんな電波（誘導電磁界と放射電磁界）がでてて大変なんですけど遠くだと放射電磁界だけなんで要するに綺麗な電磁波しかないです。そんなわけで測定は普通放射電磁界だけのとこで測ります。）。んで、2を読むとアンテナから十分遠方ってあります。この時点で1と2は相反するからどっちかが答えだなと分かります。ってことは3と4と5はあっているわけです。んで、3を読みます・・・よく分からないので次、4を読むとやっぱわからん、で5を読むとアンテナの開口面の最大寸法Ｄが波長λ以下では、フレネル領域は殆ど存在しない。とあります。2でフルネル領域は、アンテナから十分遠方の放射電界のみが存在する領域であるってあるのに5によるとフレネル領域がないことがあるそうです。フレネル領域がないってことは十分遠方がないってことになってそりゃないだろってことになります。それで、2が間違っているということが分かります。って分かりますか？
　ちなみに以上のような推測が出来なかった場合、文の最後に否定の句がある場合はあんまり正解がないようなんで私だったら2か3か4を選びます。

　これはある程度知識がないと駄目でしょう。
　まず、これだけは覚えてください。微小ダイポールアンテナの放射抵抗は

微小ダイポールの放射抵抗

　80という数字と全部が二乗されているというイメージを覚えておけばいいでしょう。
　さて、問題に戻ります。まで□Dは微小ダイポールアンテナの放射抵抗を選ぶので、選択肢は2か4になります。ここで1/2に絞れました。後は運です。
　もう少し知識があると正答が出ます。2と4で違うのは□Aだけです。で□Aは120があるかないかです。120っていう数字が出てくるのは、「Ｗ［Ｗ／ｍ²]＝」の時です。しかし今回は「Ｒ_r＝」です。したがって120がないほうなので正答は4です。
　ちなみに120が出てくるのは、ポインチング電力だけです。多分（ぉい

ポインチング電力

　この問題は知らなきゃわかんないんで運です。んでも、利得と開口面積と周波数と開口効率の問題はよく出てくる気がするので公式を暗記すべきでしょう。
アンテナの実効面積などなど

　で、このＧってのは絶対利得です。指向性利得じゃないです。でも、電波受験界を見るとなんか絶対利得として計算してます。なんででしょうか。しかしそこで疑問に思わず「まあ、そんなもんなんだな」と納得するのが早いです。こんなこといちいち疑問に思っていたら日がくれます。
　今回は開口効率ηが知りたいので、「η＝」の式になおして計算するだけです。
　η＝λ²G/4πA
　周波数3[GHz]は波長に直すと0.1[m]（波長と周波数の換算）。
　利得33[dB]を真数に直すと
　33＝10log x
　3.3＝log x
　3＋0.3＝log x
　3はlog10³で0.3はlog2なので、10³×2で、2×10³。従ってＧは2×10³。（（常用）対数と真数の換算）
　πは3.14で計算。
　η＝λ²G/4πA
　η＝0.1²×2×10³/4×3.14×2
　η＝0.8

　これも公式を知らないと分かりませんが、選択肢を見ると、0.3[μW]、3.1[μW]、32.7[μW]と桁だけ違うのが3つあります。マークシート試験でこのように桁だけ違う数字が3つ出てきた場合はその3つのうちどれかが答えです（多分）ですから私が選ぶなら1か3か5を選びます。あとは運です。
　この問題も結構よく出てくるので関連の公式を暗記して使えるとうれしいでしょう。

有効電力（アンテナが受信する最大の電力）

　Ｐ[W]（有効電力）　Ｅ[V/m]（電界）　l_e[m]（アンテナの実効長）　Ｒ_r[Ω]（放射抵抗）

半波長ダイポールアンテナの実効長

　l_e[m]（アンテナの実効長）　λ[m]（波長）

半波長ダイポールアンテナの放射抵抗　73.13[Ω]

　上の３つを組み合わせますと、Ｐ＝（Ｅλ/π）²/４Ｒ_r。
　Ｒ_rは放射抵抗なので、73.13[Ω]。
　Ｅは1[μV/m]を基準として80[dB]なので、（（常用）対数と真数の換算）
　80＝20log x
　4＝log x
　x＝10⁴
で、Ｅ＝10⁴[μV/m]＝10^-2[V/m]
　λは3×10⁸/100×10⁶＝3[m]
　これらの値をＰ＝（Ｅλ/π）²/４Ｒ_rに代入して計算して0.31。

A-5　次の記述は、図に示すようにパラボナアンテナを用いてマイクロ波無給電中継を行う場合の送受信点間の伝搬損失について述べたものである。□内にいれるべき字句の正しい組合せを下の番号から選べ。ただし、各アンテナにおける給電系の損失は無視し、区間損失は、伝搬損失と送信及び受信アンテナの利得の積の比とする。
(1)　送信アンテナの絶対利得をG_t、送信電力をP_t、無給電中継点におけるパラボナアンテナ1の絶対利得をG₁、送信点と中継点間の伝搬損失をΓ₁とすれば、パラボナアンテナ1の受信最大有効電力P₁は次式となる。
　P₁=G_tG₁P_t/Γ₁
　したがって、送信点と無給電中継点の区間損失L₁は次式となる。
　L₁=□A
　同様にして、絶対利得G₂のパラボナアンテナ2から再放射された電力をP₂、無給電中継点と受信点間の伝搬損失をΓ₂とすれば、絶対利得G_rの受信アンテナの受信最大有効電力P_r及び無給電中継点と受信点間の区間損失L₂を求めることができる。
(2)　無給電中継の送受信点間の区間損失L_trはP_t/P_rであり、無給電中継点における二つのパラボナアンテナではP₂=□Bであるから、次式となる。
　L_tr=□C
(3)　(1)(2)より、中継点におけるアンテナ利得を含めた送受信点間の伝搬損失Γは、□Dである。

　これは公式などを知らなくても、問題をよく読んでよく考えればなんとかなります。
　まず、□Dを見ます。□Dというのは伝送損失Γがどうなるかを聞いています。で、□Dの選択肢を見ると分母にΓがあるか分子にΓがあるかの違いです。普通に考えると、全体の伝送損失ΓはΓ₁とΓ₂に比例すると考えるのが自然です。だって、そりゃΓ₁が大きければ全体の伝送損失Γも大きくなるのに決まっています。したがって、答えの候補はまず3か4になります。後は運・・・と言いたいところですが、この問題はよーく読むと□Aが分かります。
　(2)の問題文に区間損失L_trはP_t/P_rでありとあります。ってことは、tからrに行くまでの損失はP_t/P_rになると言っています。ここで□Aを見てみると、区間損失L₁はとなっています。ってことは、tから1まで行く時の損失を聞いているわけです。tからrに行くまでの損失はP_t/P_rになるので、tから1まで行く時の損失はP_t/P₁になります。
　ところで、P₁=G_tG₁P_t/Γ₁です（問題に書いてあります）。そんなわけで、この式からP_t/P_rを出すと、Γ₁/G_tG₁になります。したがって、答えは3になります。
　ちなみに、□Bはどーかんがえても、P₁=P₂です。だって、無給電中継ってことは増幅しないでそのまま受信した電波を放射するってことなので、電力がかわったらおかしいですもん。
　そんなわけで、問題はよく読みましょう。結構答えがのっかっています。ついでに、他の問題をよく読むと今解こうとしている問題のヒントが見つかることがあります。問題はよく読みましょう。まー、私は問題を全部読まないで解答欄の前後しか見ないんですが

　これは公式を知らないと解けませんがよく出るので公式を知っていてなおかつ使えるようにしておくべきです。

1/4波長整合回路
のとき、
　Z₀[Ω]（特性インピーダンス）　Z_q[Ω]（1/4波長整合回路の特性インピーダンス）　R[Ω]（負荷抵抗）

平行2線式給電線の特性インピーダンス
のような平行2線式給電線の特性インピーダンスは、
　Z₀[Ω]（特性インピーダンス）　D[m]（導線の間隔）　d[m]（導線の直径）

　まず平行2線式給電線の特性インピーダンスZ₀を求めます。Dが15[cm]、dが3[mm]なので、これを公式にぶちこむと
　Z₀=277log(2×15×10^-2/3×10^-3)=277log100=277log10²=554[Ω]
　んで、Rは163[Ω]なので、Z_q=(Z₀×R)^-1/2=(554×163)^-1/2=300.5[Ω]

　これは公式を知らないと解けませんがよく出るので公式を知っていてなおかつ使えるようにしておくべきです。
　ちなみに、反射損と言っているので反射して損するわけで1が基準かなーと考えると反射損が0.41とか0.52だと1より小さいから答えは3か4か5かなーと素朴に考えると、正解する確率が3/5になります。

反射損

　M[単位なし]（反射損）　Ｓ[単位なし]（電圧定在波比）

　Sに1.5をぶちこんで計算して、1.04です。

A-8　次の記述はマジックTについて述べたものである。□内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、○1と○2は等しいインピーダンスで終端されているものとする。
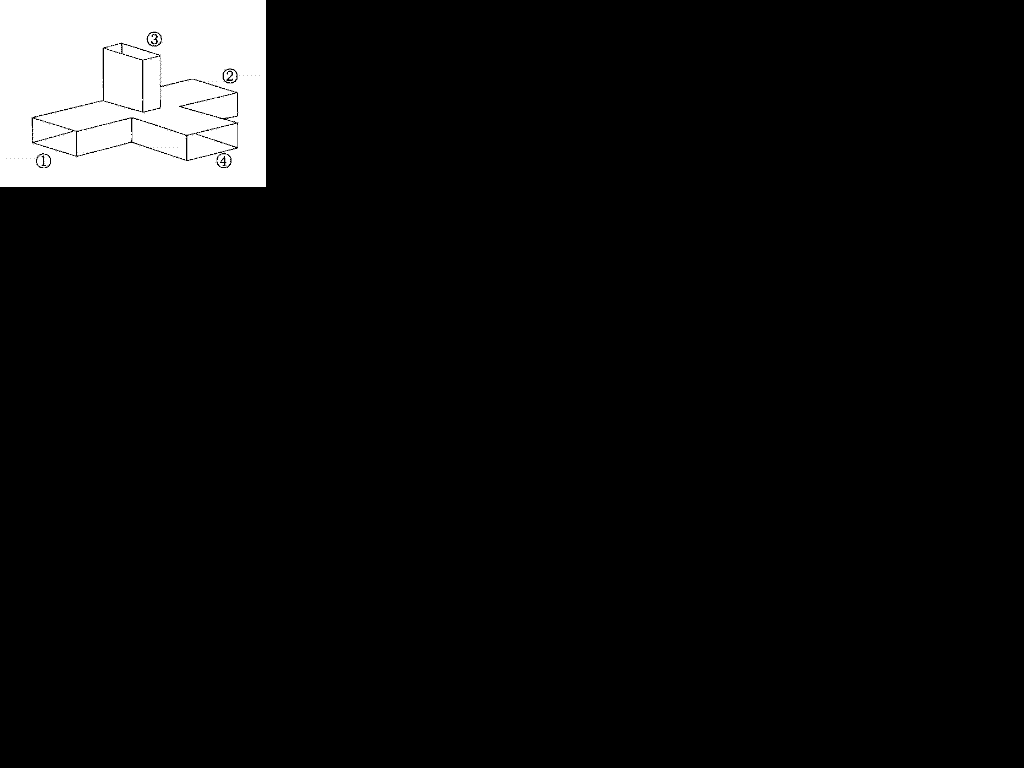(1)　○3から入力すると、○1及び○2へ□Aで均等に電力が伝送されるが、○4へは出力されない。また、○1及び○2からそれそれ反射が生じた場合、これらが○4へ入ると互いに逆位相のため打ち消し合い、○4へは出力されない。
(2)　○4から入力すると、○1及び○2へ□Bで均等に電力が伝送されるが、○3からは出力されない。また○1及び○2からの反射波は(1)と同様に、○3へは出力されない。
(3)　○3と○4の間には、結合を□C。

　知らなきゃできないです。けど、マジックTは覚えることないので覚えましょう。しかし、□3だけはし何も知らなくても「結合を生じない」を選びたくなるのが人情だと思います。だって、○3と○4は長方形の向きが違いますから。そんなわけで、選ぶなら1か2か3です。

導波管の分岐の様子（分岐する方向）

　○3から入った波は長方形の向きが同じである○1と○2にぬけます。
　○4から入った波は長方形の向きが同じである○2と○1にぬけます。

導波管の分岐の様子（位相）

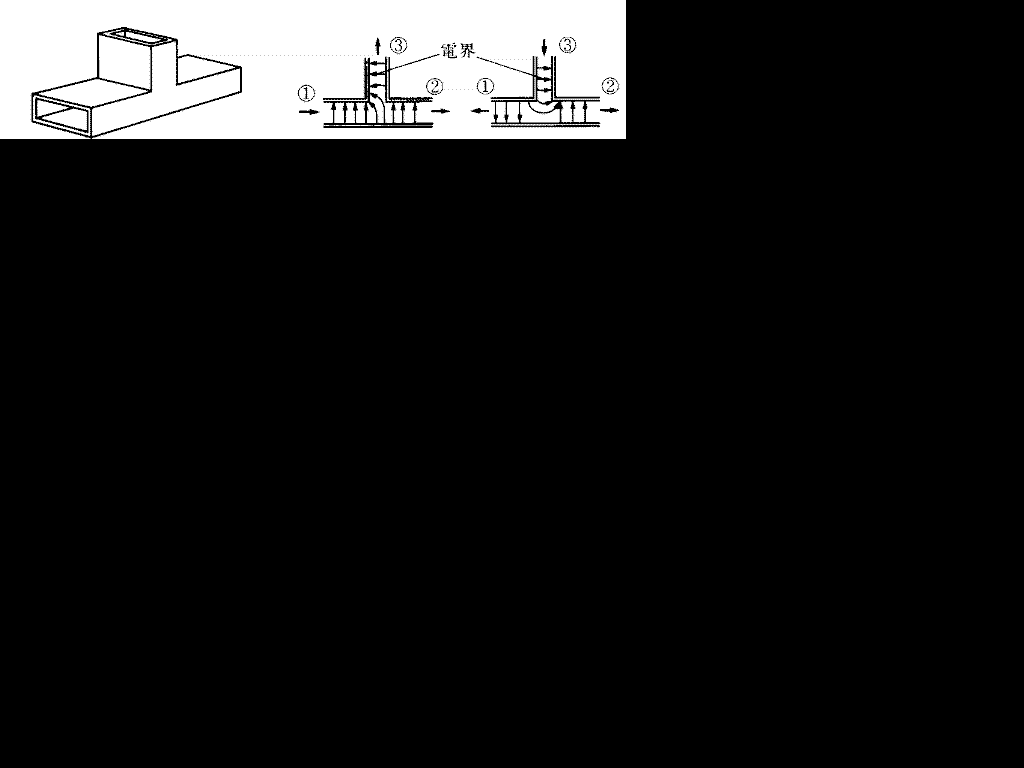
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B　東京電気大学出版局　1992　の32ページより抜粋しています。

　導波管の分岐の様子（位相）を見ると○3から入った波は○1と○2で矢印の方向が逆になっています。したがって逆位相なので答えは1です。

A-9　次の記述は、図に示す移動通信の基地局等で使用される送信アンテナの共用装置について述べたものである。□内にいれるべき字句の正しい組合せを下の番号から選べ、ただし、□内の同じ記号は同じ字句を示す。

(1)　周波数が異なる各層新装置からの出力は、それぞれの□A及び帯域フィルタ（空洞共振装置）を通った後、分岐点で合成されてアンテナへ放出される。
(2)　帯域フィルタから分岐点までの線路の長さは、各送信装置の送信周波数の1/4波長の□Bにしてあり、ある送信周波数に対して他の線路は無限大のインピーダンスではないため、その送信周波数の出力の一部が他の線路に回り込むが、回路に挿入されている帯域フィルタ及び□Aにより阻止され、他の送信装置からの□Cを阻止している。

　何も知らなくても見当がつくのは、□Bです。1/4の偶数倍か奇数倍かと聞いていますが偶数倍ですと、2/4、4/4、6/4となってこれは約分して1/2、2/2、3/2と1/2波長の整数倍と言ってもOKになってしまうのでなんかおかしいです。よって奇数倍を選びます。その前に電波には普通奇数倍という言葉しか出てきません。覚えておくと便利でしょう。ここで答えは1か5になります。あとは運です。
　電波をちょっとかじったことがあると、□Cは再放射だと分かるでしょう。スプリアス発射というのは、第2第3高調波が発射されることでこれは純粋に送信機だけの問題です。分岐点なんかがあるとだいたいインピーダンスの不整合で反射が生じ電波が再放射されます。線が分岐していたら、反射か再放射と覚えておいて間違いないと思います。
　□Aは本当に知らないとできないです。私は間違えました。インピーダンス整合器だと思っていました。しかし、考えてみるとインピーダンス整合器だと整合しちゃうので電波の出力を阻止するどころか通過させちゃいますね。したがって、アイソレータのようです。アイソレータってなんでしょうか。と思いますが「まー、こういう分岐している図を見たらアイソレータ」と私は覚えることにしています。
　結局答えは5です。

A-10　図に示す誘電体レンズアンテナにおいて、レンズの軸上の波源Oから回転双曲面上の任意の点Pまでの距離をr、Oから軸と回転双曲面との交点Qまでの距離をl、角POQをθ及び誘電体の屈折率をnとしたとき、rを表す式として、正しいものを下の番号から選べ。
1 r=l/(n cosθ-1) 2 r=(n-1)l/(n cosθ-1) 3 r=l/(1-n sinθ) 4 r=nl/(1-n sinθ) 5 (n-1)l/(1-n sinθ)

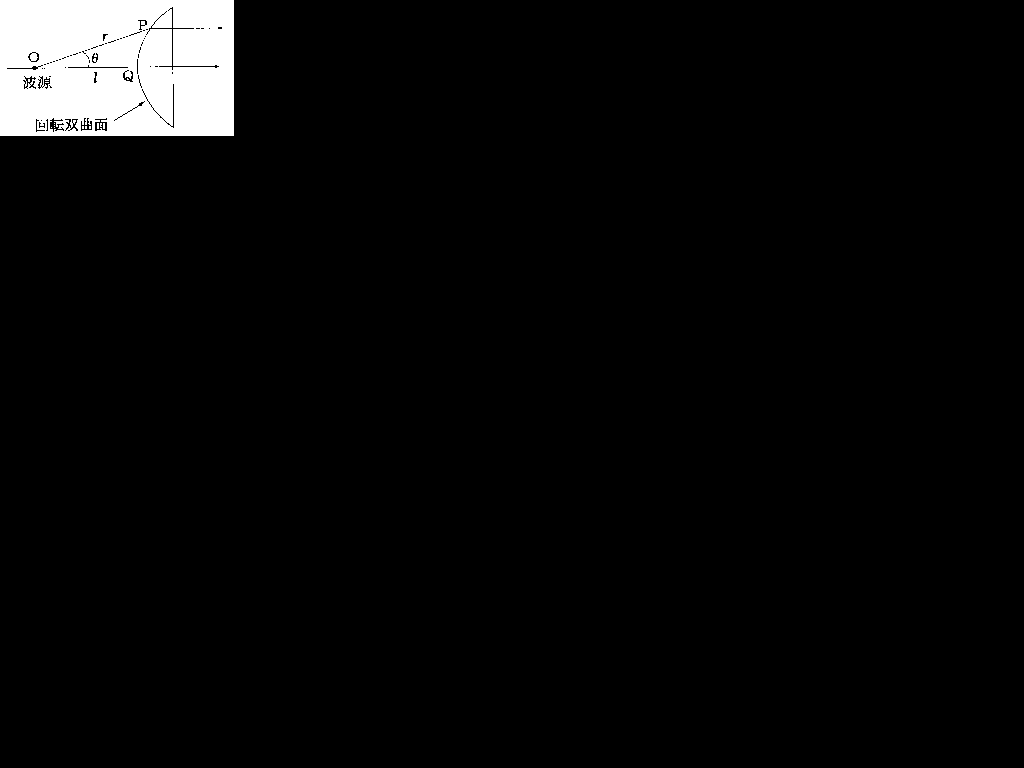
　この問題は「んなこと知るかぼけー」という感じですが、式をよーく見ると2択までもっていけます。
　点Pは双曲面の任意のところにもっていっていいので、PがQと重なった時のことを考えます。そのとき、l=rでかつθ=0です。したがってこの条件を満たす選択肢は2か3しかありません。後は運です。
　運なのですが、sinとかcosが出てきた場合はだいたいcosの方を選んでおいた方が分がいいです。したがって私なら2を選びます。正解も2なのですが。ここらへんはいい加減です。ただ私が答えにはcosの方が多いので分からなかったらcosの方を選んだ方が分がいいかなと思っているだけです。

補足
　回転双曲面は軸に対して対称になりますから、ｒを表す式は、ｒと軸のなす角θにマイナス記号をつけた−θに対しても、同じ形となります（θに関して偶関数ということ）。
　sinθは奇関数、cosθは偶関数ですから、sinθの入っている式は全部排除され、cosθの入っている式が生き残ります。
　以上、利根のカッパさんに教えていただきました。なるほどって感じです。
　分かりやすく書きます。この問題ではθのとり得る範囲は-30度くらいから+30度くらいまでです。rの値はx軸の上と下で対称です。cosθのとる値の符号(+とか-)はx軸の上と下でかわりません。θのとり得る範囲が-30度から+30度の時は常に+です。一方、sinθの場合はx軸の上では+の値をとりますが、x軸の下では-の値をとってしまいます。これではrの値がx軸の上と下で対称になってくれません。したがって、選択肢は2か3ではcosが入っている2を選ぶのが妥当です。

　この問題は知らないと分かりませんが（無論私も分かりません）文脈でなんとなく判断します。
　□Aは適当な□Aで励振するとなっています。偏波には垂直と水平しかないです。「適当な」と日本語で言った場合、「適当な値を設定する」なんていう風に「適当な」を使いますが、2通りしかない偏波と無限通り数ある電力配分比のどっちの先頭に「適当な」つけるかって言ったら、電力配分比しかないでしょう。
　次に、□Bですが複雑な一次放射器を作って何がうれしいのかさっぱり分からないので、ビームパターンを選びます。ビームパターンはいろんな形をとれた方がうれしいです。例えば携帯のアンテナなんかは電波を有効利用しないと駄目なので決まった範囲にだけ電波をふらせるためにビームパターンを決まった範囲にだけふるように設定します。多分。
　□Cはわかんないです。でもなんとなくアンテナが大きければ大きいほど狭いビームは作りにくそうな気がします。半径が1kmあるパラボラアンテナと半径が10cmのアンテナじゃどう考えても半径10cmのアンテナの方がビームが狭そうです。
　と、間違っているかもしれませんが私は以上のようなイメージで暗記します。

　この問題は5だけを読んで間違いと判断します。開口効率は、ホーンの開き角が大きいほど悪くなります。これは超よく出ます。覚えてください。開口効率をよくするためにはホーンの長さを長くするもワンセットで覚えてください。ホントよくでます。で、残った選択肢は読んでなるべく覚えるようにしてください。

　出題者が非常に苦労したんだなーと思わせる問題です。
　まず何も知らなくても分かるのが、□Dです。日本語の普通の使い方からすると、「素子数を増やすと」ときたら「何かが減る」とかがくるでしょう。そんなわけで「広く」と「狭く」とどっちを選ぶかというと、「狭く」を選びます。これで1か5の2択です。
　で、ループアンテナと言ったら一波長です。覚えてください。したがって、答えは1です。
　ちなみに、問題を当日試験会場で解くときはこうやって解けばいいですけど、過去問で勉強している時はなるべく問題文を丸暗記とまではいかないでもイメージだけはつかみましょう。

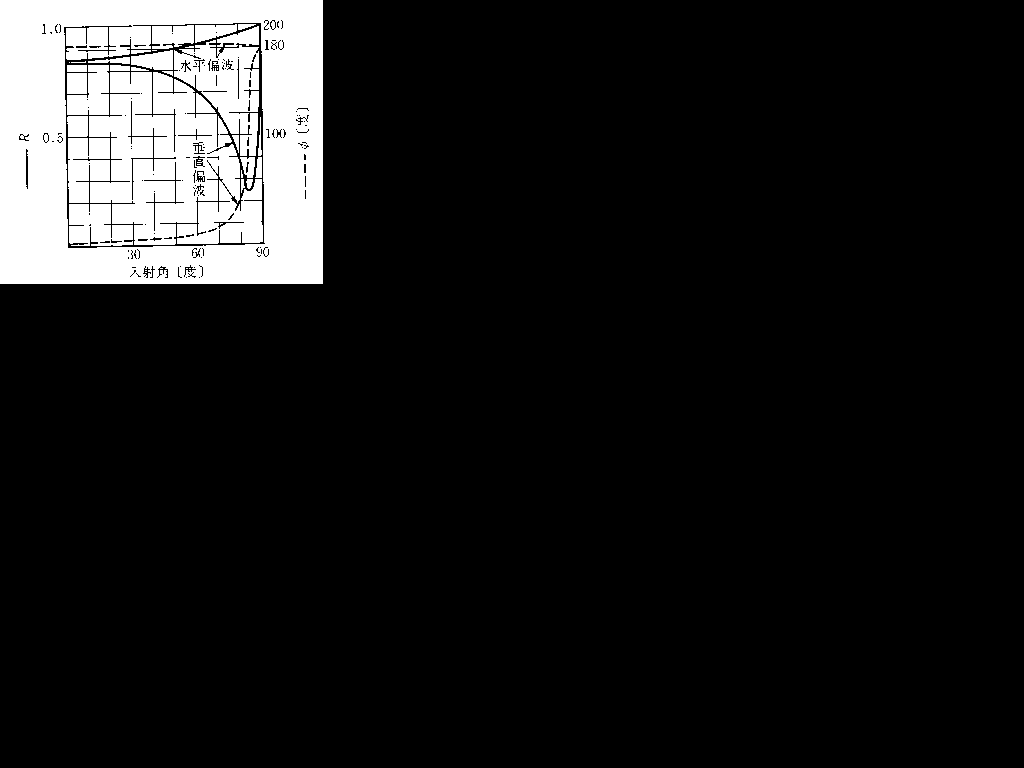　知らないとわかんないです。私も忘れてました。でも、2だけは違うかなと思いました。垂直偏波でも水平偏波でも面に対して垂直に波が入った場合、偏波が関係なくなる（だってそうですよね。絵で描いてみましょう）ので。
　あとは運です。一応右に図を載せておきます。見るべき線は実線です。これを見ると、1は確かに水平偏波の方が反射係数Rが大きいです。また2は90度の時は反射係数が1に近くなっています。3は、零にはなっていませんが反射係数が小さくなっている角（だいたい85度くらいのとこですか）があります。4は図からはわかんないですけど、覚えておきましょう。5も載っていませんが、波長は長いほど遠くまで電波が届くので反射率もいいんだなと記憶します。私は。
　答えは5だそうです。
　右の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B　東京電気大学出版局　1992　の158ページより抜粋しています。

　これは公式にいれて解けそうかな〜と思ったのですが、実は解けませんでした。普通は電離層への入射角や到達距離が与えられているのですが、この問題は見かけの高さしか与えられていないです。
　緑色の点が反射点とします。適当な角度α電波をうつと、反射して地面に帰ってきます。

　今度はαより小さい角度βで電波をうつと、遠くまで電波が届きます。ということは、どんどん角度を小さくしていけば、電波が遠くまで届くはずです。しかし、角度を小さくするのには限界があります。それは地球が丸いからです。

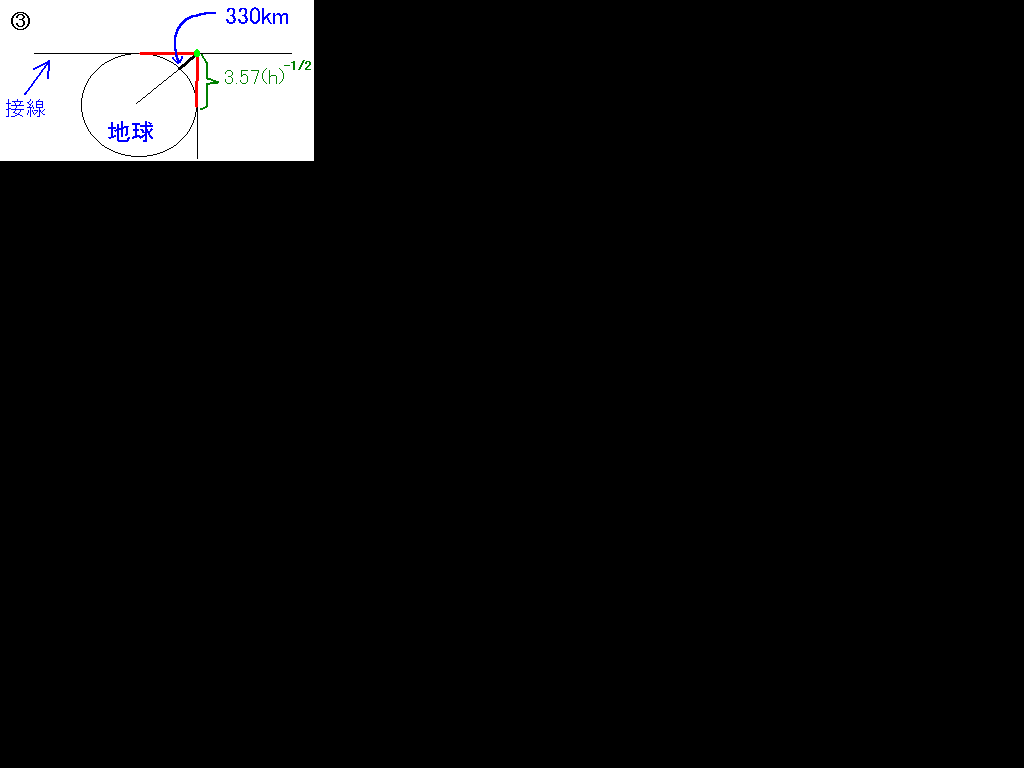　結局左の図のようになります。赤い線が電波の通り道、緑色の点が反射点です。この電波のはなたれた角度より小さくすることは出来ません。地球が小さく書いてあるので分かりづらいと思いますが、実際には電波は地平線すれすれにうっています。あと、左図の(h)^-1/2は(h)^1/2の誤りです。間違えました。

　電波をアンテナから地平線に向けてうった時、どのくらい届くかの距離は公式があります。

幾何学的見通し距離（アンテナが1つの場合）
　
　地上高h₁[m]のアンテナ　見通し距離d₁[m]

　問題では電波が反射する点が緑色の点です。こっから電波が発射されていると考えると、地上高330kmのアンテナから地平線に向かって電波を発射しているのと同じです。そんなわけで、h₁に330kmを代入して計算し、その値を2倍にしたものが答えです。なんで2倍になるかというと、上の○3の図を見てください。
　だいたいd₁が2050kmなので、答えは2倍して4100kmで、4を選びます。
　ちなみに、大気の屈折率を考えると答えが4700kmなので答えは○5になるんですけど、どうなんでしょうか。電波受験界は答えを4000にしているんですけど信用していいんかなあ。

　公式を知らないと出来ませんが、よく出る問題なので解けるようにしておくべきです。

自由空間伝搬損失Γ

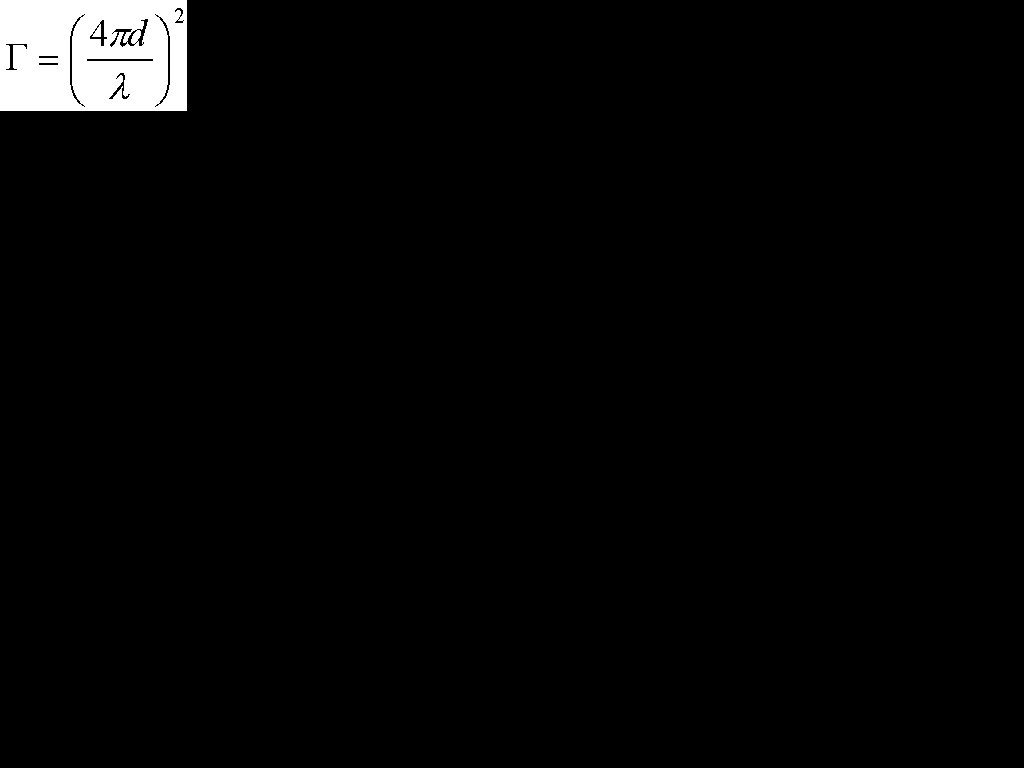
　Γ［単位なし］（自由空間伝搬損失）　d［m]（距離）　λ[m]（波長）
　ΓはdBになおして使用することが多いです。その時は、10log₁₀Γです。

デシベル計算の場合
　P_t[dB]=P_s[dB]+G_s[dB]+G_t[dB]-Γ[dB]
　受信電力=送信電力+送信アンテナの利得+受信アンテナの利得-自由空間伝搬損失

　こういう問題を一回も解いたことがないための方に図で説明。
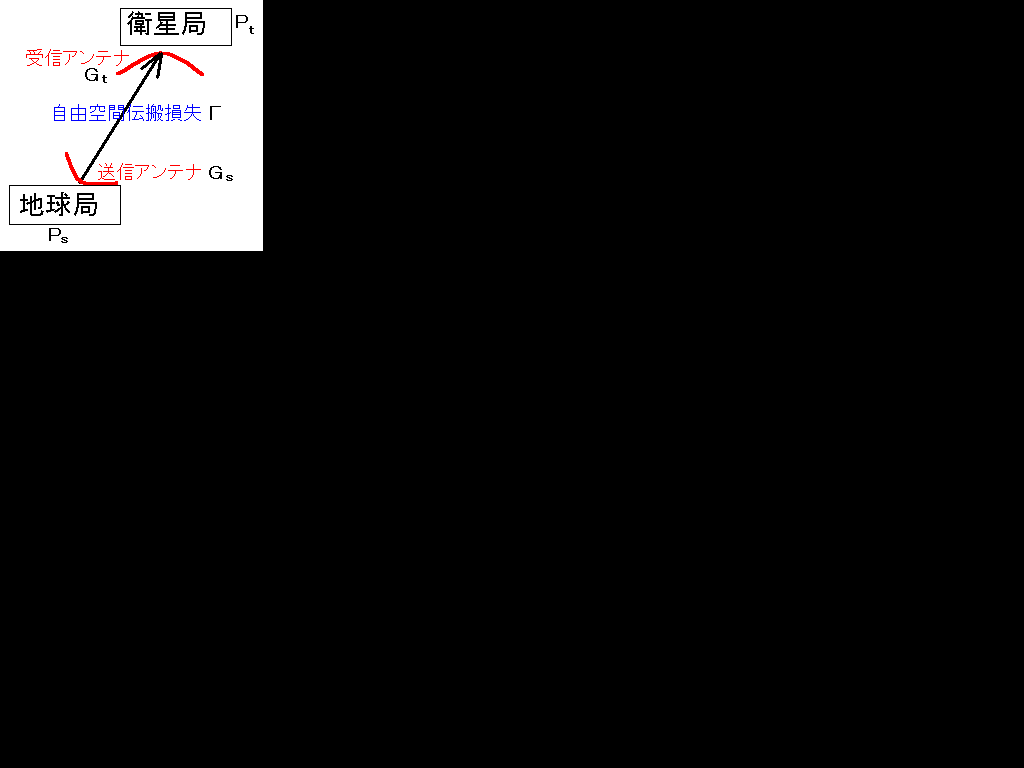　まず、送信局はP_sの出力で電波を出します。送信アンテナは、送信利得G_sで電波を増幅して電波を出します（嘘かもしんないけど、私はそういうイメージで記憶しています）。だから、P_sにG_sを足します。次に電波は空間を通っていると減衰します。その減衰分が、ΓですのでΓを引きます。次に、受信アンテナの利得G_t分だけ電波が増幅されるのでG_tを足します。その結果がP_tです。

　まず伝搬損失Γを出します。デシベルで求めます。
　λ=3×10⁸/10×10⁹=0.03
　Γ=10log(4×π×36000×10³/0.03)²
　　=20log(4×π×36000×10³/0.03)
　　=20log(15×10⁹)
　　=20log15+20log10⁹
　　=20log3+20log5+180
　　=9.5+14+180
　　=203.5
　次に計算に入ります。
P_t[dB]=P_s[dB]+G_s[dB]+G_t[dB]-Γ[dB]
-90=P_s[dB]+59+20-204
P_s[dB]=35
35=10logP_s[真数]
P_s[真数]=10^3.5
　　=10³×10^0.5（10^0.5は10ルートのことです。）
　　=10³×3.2
P_s[真数]=3200[W]　なので、答えは3。なんですけど、log5なんか覚えているかぼけーと思いました。みなさんは覚えておきましょう。

　何も知らなくても分かりそうなのが、□Bです。回折型と銘打っているので電波が回折するんだなと思います。回折と関係がある言葉は屈折でしょう。減衰は電波が弱くなるだけで曲がったりしません。よって2か4です。後は運です。
　そして、クリアランスという言葉は知っておいて損はないです。本当の意味は知りませんが、クリアランスをとる、というのは電波の伝搬経路をふさがないようにする、ということだそうです。フェージング率という言葉は多分ないです。したがって、（当たり前ですけど）知っていれば2を選べます。

　直接波が山岳などのナイフのようにとがった障害物にあたると回折してしまって受信点では回折波と直接波が干渉を起こします。そこで、回折が起こらないように第一フレネルゾーンに障害物が入らないようにします。

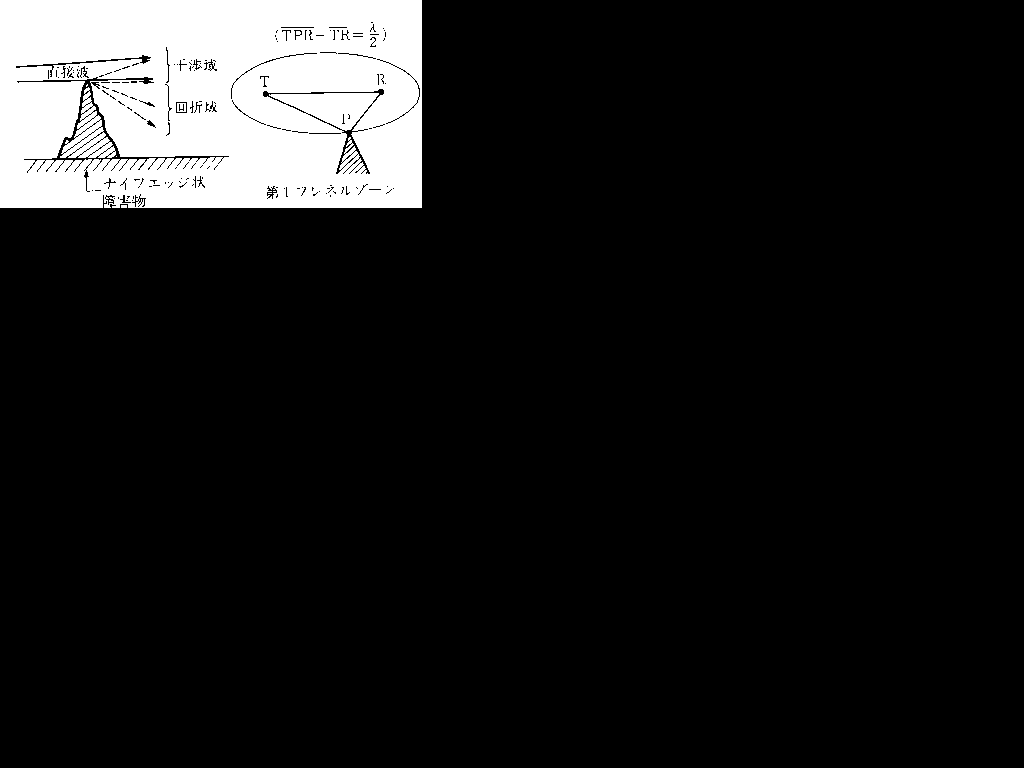
上の図は吉川忠久著『2陸技1・2総通受験教室○4』無線工学B　東京電気大学出版局　1992　の158ページより抜粋しています。
　電波が第一フレネルゾーンに入らないようにすることをクリアランスをとると言います。
　もしかしたら、第一フレネルゾーンを求める計算が出るかもしんない（昔は出てた）ので、式も覚えておくとうれしいかもしんないです。第一フレネルゾーンは楕円形をしています。焦点2つありますので。

　まず、アンテナと言ったら可逆性です。非可逆性を選ぶことは絶対にないです。可逆性を選んでください。したがって、選んでいいのは1か3か5です。
　次に、開口面アンテナの測定距離の最小距離と言ったら、

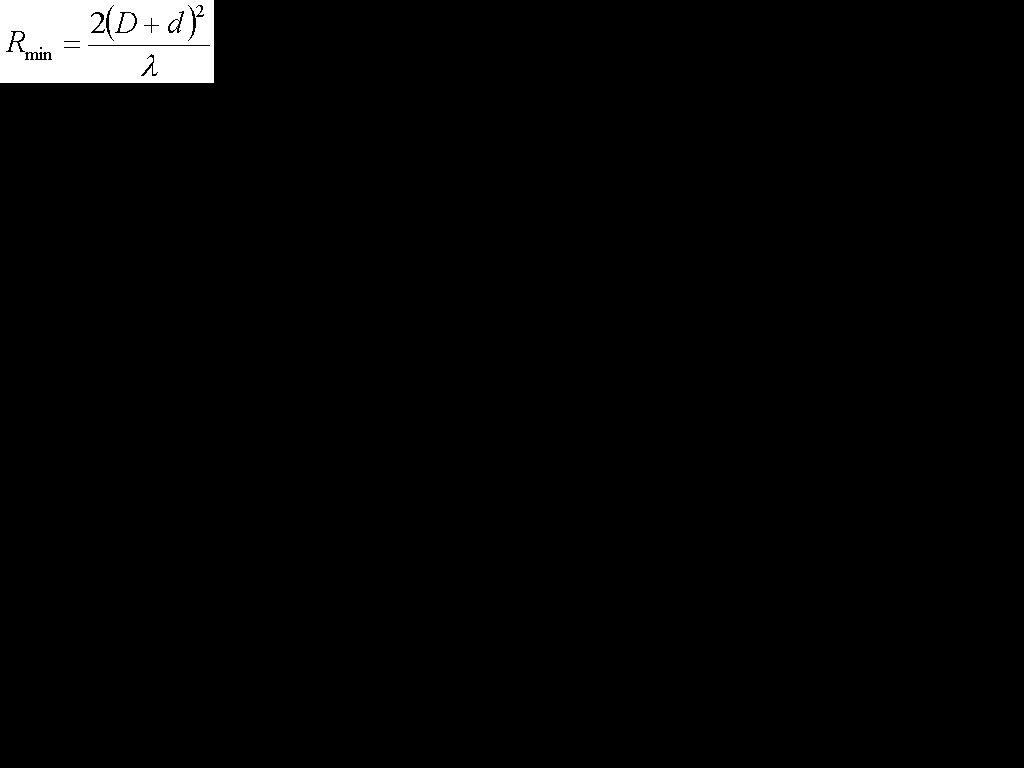
です。吉川忠久著『2陸技1・2総通受験教室○4』無線工学B　東京電気大学出版局　1992には、

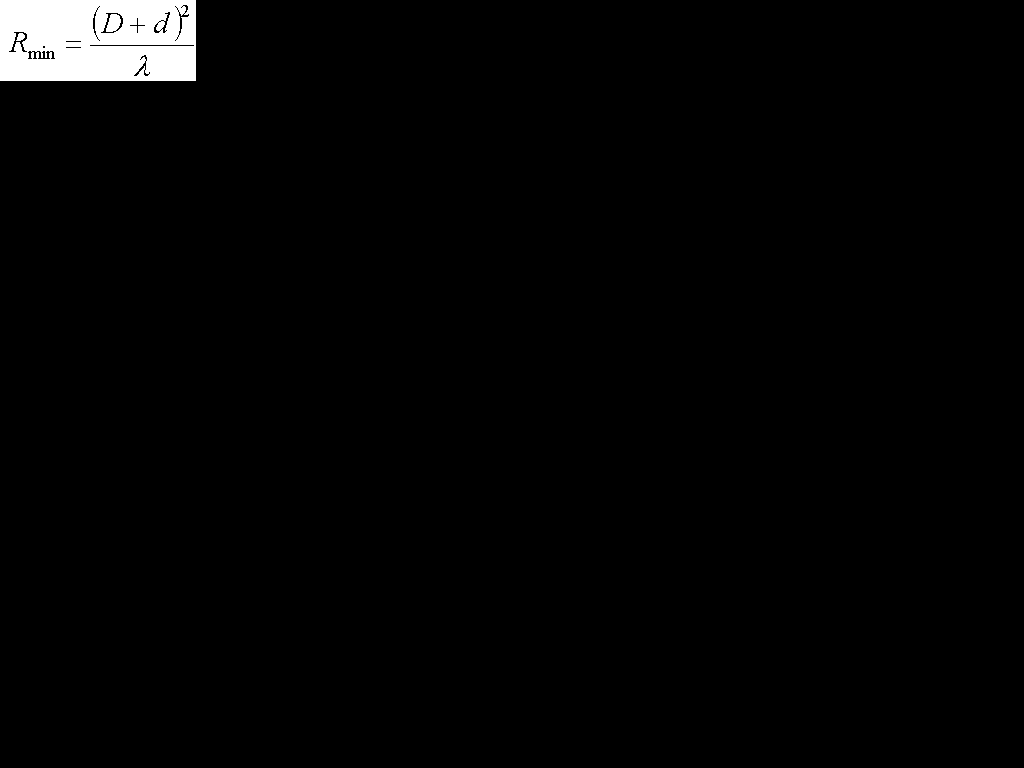
の時に、誤差が小さく出来ると書いてあります。私もこっちだと思っていたのですが、誤差が2%と書いてあると式の最初に2がつくようです。まあ距離が離れていた方が誤差が小さそうなので2がつくと考えておいた方が無難でしょう（ホントか？
　そして、□Dですがオープンサイトとボアサイトを比べると明らかにボアサイトの方がうさんくさそうですし、オープンな方がなんか障害物がなさそうです。したがって、オープンサイトを選びたくなります。
　ちなみに答えは5だそうです。

　さて、さっぱりわからないのは確かですが、反射係数Γの求め方だけはよく出るので知っておくべきです。

反射係数

　S[単位なし](電圧定在波比)　Γ[単位なし](反射係数)

　そうすると選べる答えは1か2か3になります。んで、スロットアンテナの図を見ると分かるんですが、どうみてもスロットは移動しそうにないです。したがって、□Aはプローブだなと思います。あとは運です。答えは1だそうですが、なんでそうなるのかわからないです。
　さて、次が問題です。この次に同じような問題が出たときは解答できるとうれしいです。そこで私はこの問題の場合は□Dの式には2がついていると覚えます。頭に入れるのは、溝付き伝送路は管内波長の式に2がついていた、です。多分これだけ覚えておけば十分でしょう。なんでかと言うと無線の試験において、式を選ばされるときは係数が違うか文字が2乗されているかいないかの違うくらいです。したがって係数と何乗されているかを覚えておけば細かい部分は覚えている必要はありません。計算しなければならない問題の場合は正確に式を暗記しますが、A-19のような問題は絶対に計算させられることはないです。

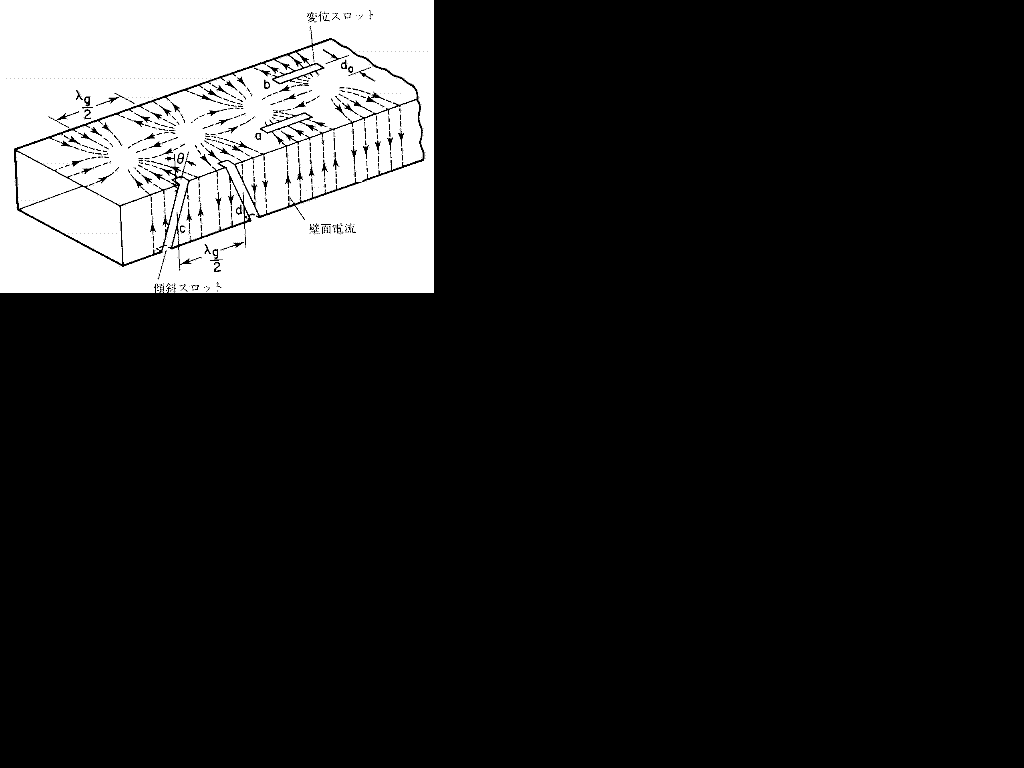
F・R・コナー原著　安藤真訳『電子通信工学シリーズ4 アンテナ入門』森北出版株式会社　1990の81ページより抜粋
　ちなみに上のスロットアンテナの図を見ると、スロットの間隔がλ_g/2になってますよね。とすると、λ_g=2(ここになんか式がくる)となるので、なんか式の右辺に2がくるような気もします。ホントかどうか知りませんけど。嘘臭いですね・・・

　まず常識で考えて、1は違うでしょう。5もなんか正しそうな気がします。測定器は電波がなるたけ届かないところの方が誤差が少なさそうです。したがって、選ぶなら2,3,4です。
　答えは、3だそうです。確かに本を見ると「定在波測定器はマイクロ波を測定する(導波管に穴をあけて測定するから、確かにマイクロ波しか測定できなさそう)」ものなのでそうみたいです。ちなみに、否定の語句が含まれるのは3だけなので、3,4,5のどれを選べと言われたら3を選んだ方が良いです。否定の語句が入っているものに正解は多いです。
　答えが、3と分かったら、正解の文章を頭に焼き付けます。例えば、2は「ああ、アンテナが高いと給電線が長いから抵抗が大きくなったら、インピーダンス高いかなあ」と記憶します。4は「VHFと2波長」という言葉だけ頭にいれておいて、同じような問題が出てきたら、「VHFはなんだかわかんないけど、2波長だったなあ」と思い出します。

B-1　次の記述は、全く同じ二つのアンテナの指向性を合成した指向性について述べたものである。□内に入れるべき字句を下の番号から選べ。ただし□内の同じ記号は、同じ字句を示す。
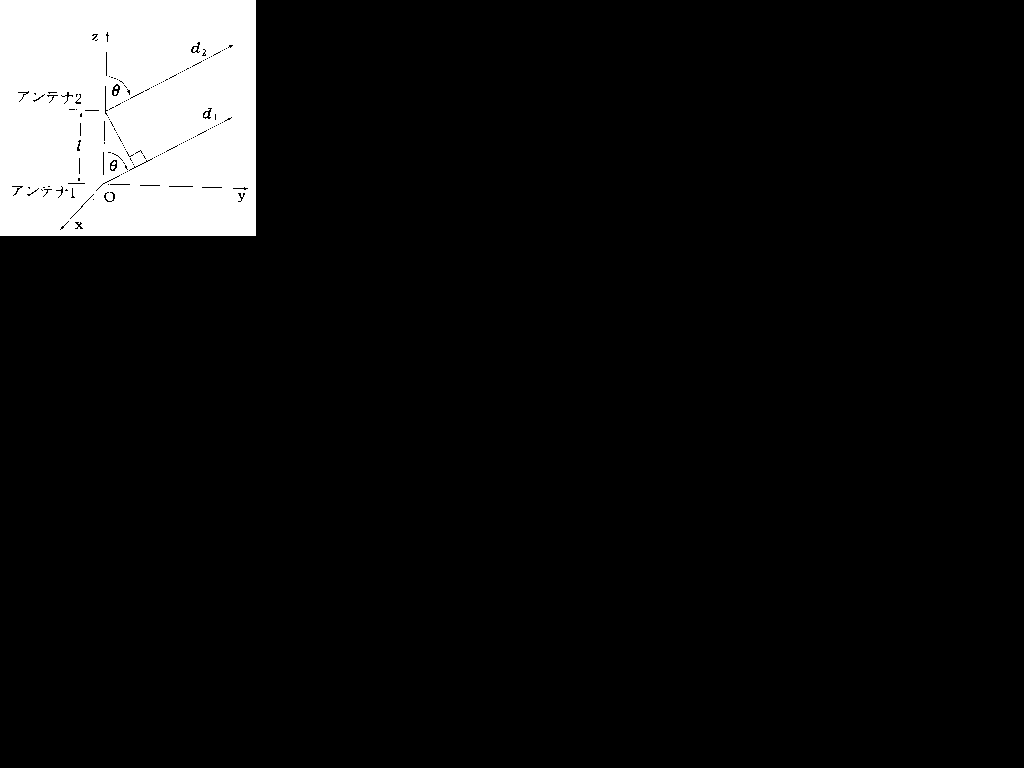(1)　図に示すように、アンテナ1を原点Oに置いたとき、遠方の距離d₁の点における放射電界E₁は次式で表されるものとする。ただし、アンテナ1は微小電気ダイポールとし、Dをアンテナ素子の指向係数とする。
　・・・○1
(2)　アンテナ1と同じアンテナをz軸方向にlだけ移動して置き、これをアンテナ2とすれば○1式のd₁はd₂となるから十分遠方では、○1式の距離に関係する項は次式となる。ただし、θは図に示すようにとるものとする。
　
　また、一般に、アンテナにm倍の電流を流した場合、放射電界は、位相を含めて元のアンテナの□イ倍となる。
　したがって、アンテナ2にm倍の電流を流したときの放射電界E₂は次式のようになる。
　
(3)　(1)及び(2)より、アンテナ1の放射電界E₁と、アンテナ2の放射電界E₂との合成の放射電界E_tは次式となる。ただしD_tは二つのアンテナの合成した指向係数とする。
　
　上式から、1+□ウは、強さが1及び□イと二つの無指向性点放射源互いにlだけ話して置いたときの指向性係数であると考えることが出来る。
　したがって、二つのアンテナの合成した指向性係数D_tは、アンテナ素子の指向性係数Dと無指向性点放射源の指向性係数との□エになる。
(4)　一般に、指向性が全く同じアンテナを並べたときの合成した指向性は、アンテナ素子の指向性係数と無指向性点放射源の配列の指向性係数との□エで表される。これを指向性の□エの原理あるいは□オの原理という。
1　　2　点放射源合成　3　m²　4　　5　m

6　m²e^jβsinθ　7　指向性合成　8　積　9　me^jβcosθ　10　和

　まず□エと□オからいきます。入れるのが日本語なので。□エですが、指向性は積です。和と積がありましたら積を選んだ方が無難です。指向性係数とありますが係数を足すということはないです。次に、□オですが指向性合成です。指向性の話をしているのに、点放射源が出てくること自体よくわかりません。
　ここで残っている選択肢は、1,3,4,5,6,9です。これを仲間分けします。1と4、3と5、6と9に分けます。似ているものでくくればいいだけです。
　さて、次に分かりそうなのは□イです。アンテナにm倍の電流を流したら、放射電界は何倍になるかということです。これは、3か5を選ぶってのは分かります・・・ね。で考えます。オームの法則によると、電流が2倍になったら電圧も2倍ですよね。アンテナだって同じです。電流がm倍になったら電圧もm倍です。したがって放射電界のm倍です。m²倍になったら夢のエネルギーじゃないですか？　電流2倍になったらなぜか電界が4倍になるんですよ。おかしいですね。
　□イが分かると、□ウが自動的に分かります。□イはmなので、6と9のどっちを選ぶかと言ったら、9しかないです。なんで、1と4は選ぶ対象に入ってこないかと言いますと、「m」が式に入っていないからです。□ウの前の文章を読むと、「アンテナ2にm倍の電流を」と書いてあります。したがって□ウの式にはmがはいっているべきです。
　で、□ウが分かると□アが分かります。□ウでは、9を選びました。これは、式を見るとcosθが入っています。したがって□アの時点でcosθが入っていないとおかしいです。1と4のどちらを選ぶかと言ったら、1しかないです。

　さて、一件難しいように見えますが、オームの法則だけを知っていれば□アと□イと□ウは出来ます。□エと□オは無線の常識なのでぜひ覚えてください。

ア:1 イ:5 ウ:9 エ:8 オ:7

　まず、□アと□イは陸特でもよく出る問題です。ぜひ覚えてください。TEM波は電界と磁界の方向が共に直角です。普通の電波はTEM波です。次に、導波管と言ったらTE波です。TE波は電界が伝送方向に対して直角です。
　□エですが、文脈から判断すると「持ち」と「持たず」どちらが入るかと言ったら「持ち」でしょう。「持たず」だと何か文が変です。ここで(3)では、マイクロストリップ線路はハイブリッドモードであると書いています。したがって、□ウにいれるのは「導波管」です。マイクロストリップはハイブリッドモードなのですから。
　□オは運です。
　ちなみに、マイクロストリップ線路については、第二級陸上無線技術士試験の平成9年1月のB-4に出ていますので、環境があれば本屋さんで立ち読みしてみましょう。

ア:1 イ:2 ウ:3 エ:5 オ:8

B-3　次の記述は、図に示す対数周期ダイポールアレーアンテナについて述べたものである。このうち正しいものを1、誤っているものを2として解答せよ。
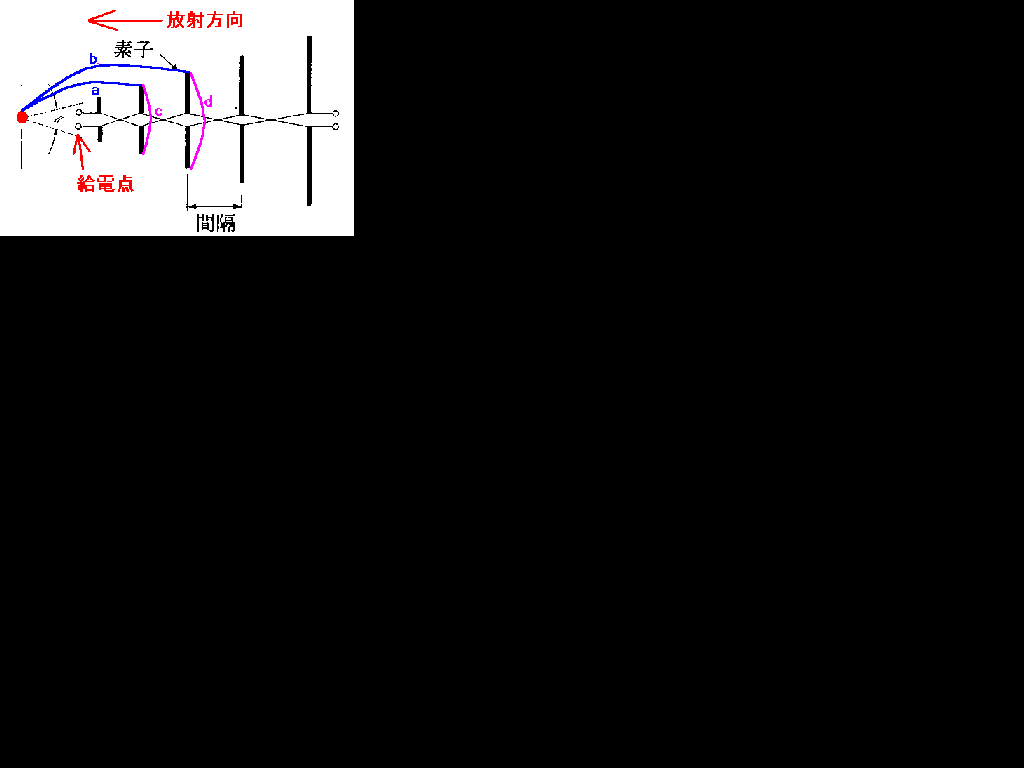ア　入力インピーダンスや放射特性などが、周波数の対数に比例して繰り返す構造である。
イ　隣り合う各素子間の間隔の比と素子の長さの比は等しく一定である。
ウ　各素子の両端を順次連ねてできる二本の直角に交わる角αと各素子の長さの比を適当に選べば、指向性は単向性となる。
エ　バックファイアアンテナであるため、給電点方向に向かって電波が放射される。
オ　使用可能な最低周波数と最高周波数の比は1対10まで広くでき、利得は十数デシベルである。

　これは勘では出来ないです。対数周期ダイポールアレーアンテナはよく出ます・・・と思ったら私の持っている過去問には一回しか出てませんでした。でも、計算いらないのでキーワードのイメージだけ頭に焼き付けましょう。
　まず下に書いてある答えを見て、ああ、そんなもんなんだなと思ってください。まず、アですが「対数に比例して」と書いてあるので、対数周期アンテナなんだからそうだよなあ、と私は思います。次にイですが、よく出る気がします。隣り合う素子間の間隔の比ではなくて、図の赤い点から素子までの距離の比です。多分、b/a=d/cです。ウですが「んー、そんなもんかな」と納得して適当に調整すると単向性になると記憶します。エですが、私は間違えました。しかし、八木アンテナを知っていると確かに素子が短い方に電波が飛ぶので給電点方向に電波が飛ぶ、と記憶します。オですが、周波数の比は1:10はあっていますが、利得は数デシベルだそうです。

ア:1 イ:2 ウ:1 エ:1 オ:2

　まず□アは、見通し図と伝搬図のどちらかです。伝搬の状況をこれから調べるのに、伝搬図を使うのはおかしい気がするので見通し図を選ぶのが自然です。
　□イは垂直か水平を選びます。屈折率というのは空気の密度でかわります。空気は上にあがるほど密度が小さくなっていくので、垂直方向では屈折率はかわってしまいます。ですから、水平です。
　□ウは大きくか小さくを選びます。地表距離と高さでは地表距離の方が圧倒的に長いので地表距離の縮尺を大きくしないと紙におさまりきらないのはちょっと考えれば分かります。したがって、nが大きくないと駄目です。
　□エは□エの前に「地球大地面の弧は円弧ではなくなるが」ときているので、円弧ではなく「直線」を選ぶのが自然です。
　□オですが、私は間違えました。日本語としては文脈から考えて「同じになる」だと思いました。しかし、考えると縮尺した図の交差角と実際の角が等しくなるはずがないです。したがって「異なる」を選ぶべきでした。

ア:9 イ:2 ウ:3 エ:10 オ:1

　ちなみにプロフィル図の一例を下記に示します。

B-5　次の記述は、図に示す構成により、開口が円形のマイクロ波アンテナの絶対利得を測定する方法について述べたものである。□内にいれるべき字句を下の番号から選べ。
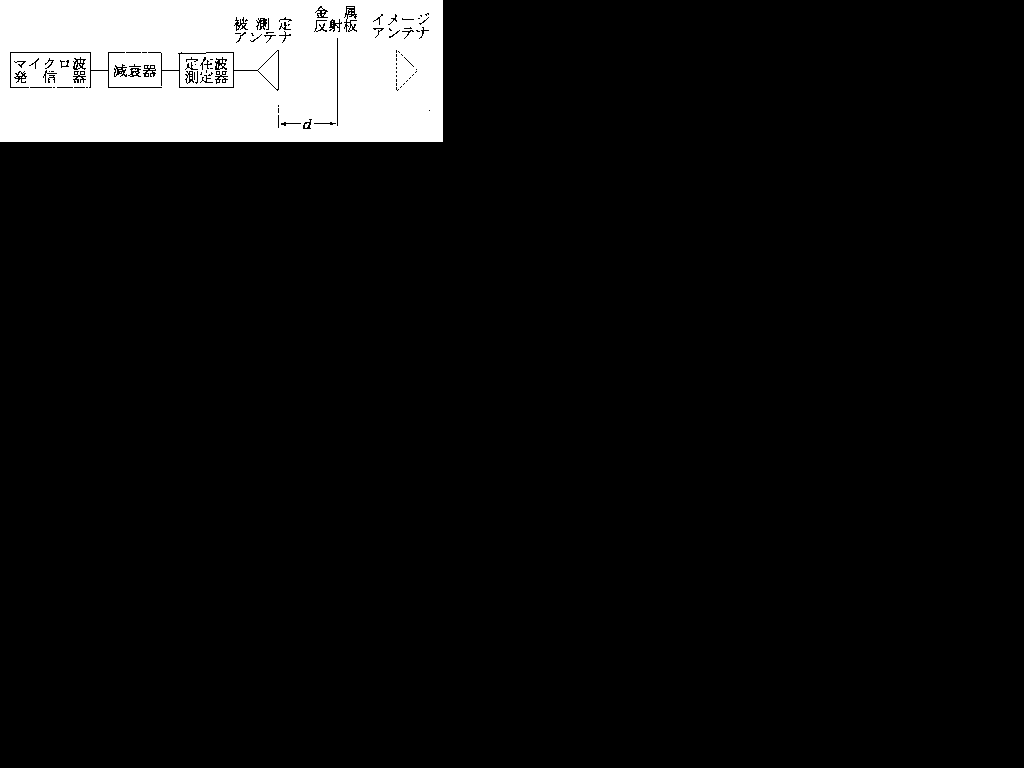(1)　被測定アンテナの開口面から距離d[m]の位置に、アンテナに正体させて金属反射板を置き、定在波測定器を通して電波を放射する。ここで、アンテナと反射板との距離dは、アンテナの直径をD[m]、波長をλ[m]とするとd>=□アとなるようにする。ただし、dは、電界強度が弱くなりすぎない程度の大きさにする。
(2)　被測定アンテナの絶対利得をG(真値)、放射電力P_t[W]とすれば、イメージアンテナの位置における電力密度は、□イ[W/m²]であるので、受信電力は実効面積λ²G/(4π)[m²]との積として□ウ[W]となる。この電力が反射板によって反射されて反射電力P_r[W]として被測定アンテナに戻る。
(3)　反射電力と放射電力の比P_r/P_tは、電圧反射係数の2乗に等しいので、(2)から、電圧反射係数の絶対値は□エとなる。この電圧反射係数は定在波比によって表すことが出来るから、定在波測定器で電圧定在波比Sを測定すれば、比測定アンテナの絶対利得Gは、□オと表される。
1　2D²/λ　2　(λG/8πd)²P_t　3　4πd(s-1)/λ(S+1)　4　GP_t/16πd²　5　λG/4πd
6　λG/8πd　7　D²/λ　8　8πd(s-1)/λ(S+1)　9　(λG/4πd)²P_t　10　GP_t/8πd²

この問題は超よく出ます。この問題だけは自分で手を動かして式を最初から最後まで導出できるようにしておけるとうれしいです。まあ、そこまでしなくても式のイメージをつかんでおけば大丈夫といえばそうですが。

□アは「アンテナの直径をD[m]、波長をλ[m]とすると」と書いてありますので式の中にDとλしか出てきてはいけないです。したがって、選べる選択肢は1か7になります。

開口面アンテナの測定距離の最小距離(誤差2%程度)

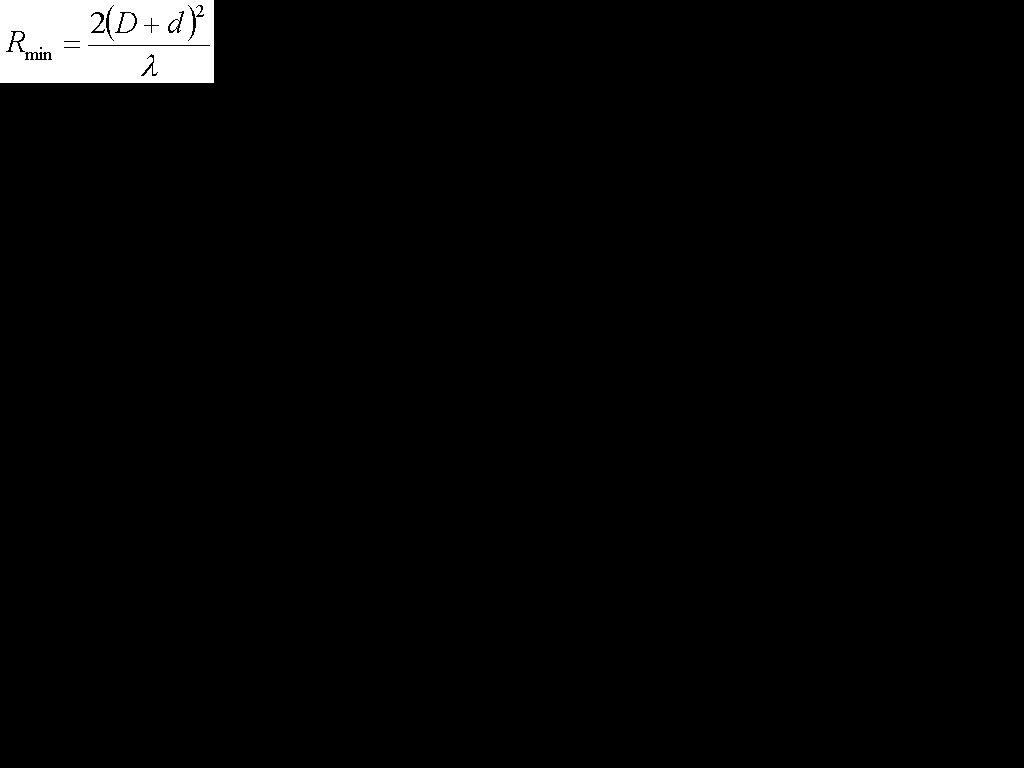
　R_min[m]（最小距離）　D[m](アンテナの直径)　d[m](アンテナの直径)　λ[m](波長)

　今回は上の公式のR_minがd、上の公式のdは受信、送信とも直径Dのアンテナを使うのでdはDです。したがって、d=2D²/λになる・・・としたいですけど、実は電波が飛ぶ距離は2dです。反射板で反射して電波が帰りますので。したがって距離は2dとなりますので、2d=2D²/λでd=D²/λで答えは7です。
　□イと□ウは一緒に考えます。本当にこの問題をちゃんと解くならば以下の公式を暗記している必要があります。

マイクロアンテナの受信点の電力密度（重要）

　W₀[W/m²](電力密度)　P_t[W](送信電力)　G_t[単位なし](送信アンテナの絶対利得)　d[m](送信アンテナからの距離)

　今回は、上の公式のdの部分が2dにならないと駄目なので、答えはGP_t/16πd²になります。そして、□ウは実効面積λ²G/(4π)[m²]を□イの答えにかければいいので簡単に答は出ます。これが正当派。
　公式を知らなくとも解けます。まず□イに入りそうな選択肢ですが、「被測定アンテナの絶対利得をG(真値)、放射電力P_t[W]とすれば」とあって(1)の問題でdが出てきていますので、この3変数が含まれているものです。候補は、4,10です。□ウは□イにλ²G/(4π)[m²]をかけるので分子にλ²があるやつです。候補は2,9になります。
　そして下の画像をご覧下さい。

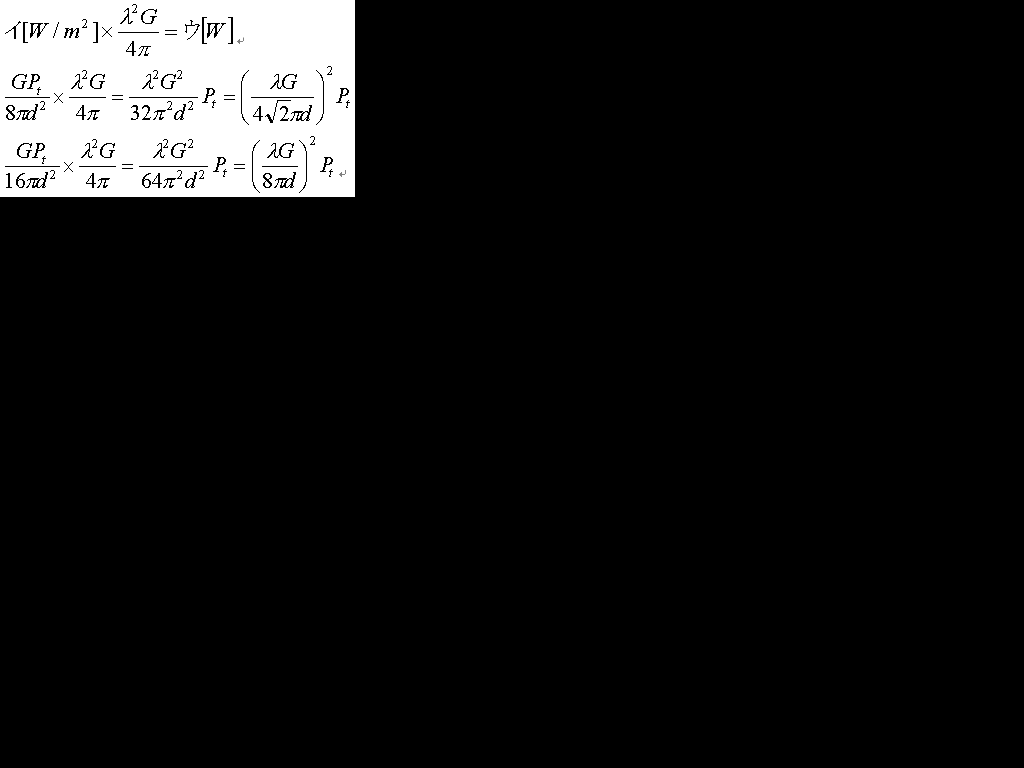
　もしイに選択肢10のGP_t/8πd²をいれてしまうと、上から2番目の式のように分子にルートが出てきてしまいます。一方、選択肢4を選ぶと上から3番目の式のように綺麗になります。したがって□イは4、□ウ2です。
　□ウが分かれば、必然的に□エは分かります。「P_r/P_tは、電圧反射係数の2乗に等しい」と書いてあるので、P_r/P_t=の式を作ってみると、

　よって答えは、6になります。
　□オはすでに、□エの答えの分子に8πλがあるので、8を選びたくなるのが人情だと思います。
　ちゃんとやると、電圧定在波比と電圧反射係数の関係は、

電圧定在波比と反射係数の相互変換(重要)

　S[単位なし](電圧定在波比)　Γ[単位なし](反射係数)

　という関係があるので、

のΓにいれてみてください。

ア:7 イ:4 ウ:2 エ:6 オ:8

平成8年7月

　だいたいの場合、赤字で書いたところのように否定の部分がある選択肢は自信がない限り選ばない方がいいです。そんなわけで今回選んでいいのは1か5だけです。あとは運です。しかし、半値幅の問題を解いたことがあると「あー、半値幅のところには波長って言葉があったなー」と思い出すと5を選ぶことになります。
　3番は、どう考えてもそこらにあるパラボラアンテナは宇宙向いているので雑音を受けそうですし、4番はアンテナは受信と送信で指向特性が違うのはないです。そんなわけで、3と4は絶対に選んではいけません。

　知っていると1を読んだ時点で1です。等方性アンテナと絶対利得はワンセットで覚えましょう。
　まず、4と5は否定の言葉が入っているので切り捨てます。あとは知らなければ運です。指向性は十分遠方では方位（っていうか角度θ）にのみ比例することを覚えていると2を切り捨てられます。で、3番は「んー、これcosかなー、sinかなー」と考えます。あとは運ですね。