2001年8月9日
陸上無線技術士(無線工学B)
概観
陸上無線技術士の無線工学Bにおいて三角関数を使う機会は少ないです。三角関数を1から学んでいる暇があったら別の勉強した方が良いと思えるくらいです。
また三角関数を説明するためのいい例がないです。ここを読みこなすには相当の知識が必要でしょう。
今のところ優しくて役に立つのは平成12年7月 2陸技 無線工学BのA-15だけです。
実践
平成12年7月 1陸技 無線工学BのA-4
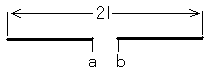
図に示す長さが2l[m]の半波長ダイポールアンテナの特性インピーダンスが420[Ω]であるとき、給電点abから見たインピーダンスを純抵抗とするためのアンテナ素子の短縮率として、最も近いものを下の番号から選べ。ただし、位相定数をβ[rad/m]とすれば、長さ2lで特性インピーダンスZ
0[Ω]のアンテナのab端子から見たインピーダンスZ
abは、次式で与えられるものとする。
Z
ab≒73.1+j42.6−j2Z
0cotβl
また、Δが小さな値のとき、次式の関係が成り立つものとする。
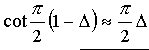 1
1 1.6[%]
2 2.0[%]
3 2.4[%]
4 3.2[%]
5 4.8[%]
- 短縮率
- 短縮率
短縮率を求める場合は虚数部分(jがついている項)を0にします。
この問題ですと、虚数部分は j42.6−j2Z0cotβl ですので、2Z0cotβlの部分が42.6になるようにします。そうすると、j42.6−j42.6=0になって虚数部分が消えますよね。
- 半波長ダイポールアンテナ
- アンテナの長さが波長の半分であるアンテナのことをいいます。
この問題はcotが出てきていかにも三角関数の知識がないと駄目なように見えますが、知識はいりません。
半波長ダイポールアンテナなので、2l=λ/2です。したがって、l=λ/4です。
βは位相定数です。β=2π/λです。これは決まりです。
Zab≒73.1+j42.6−j2Z0cotβlにlとβを代入すると、Zab≒73.1+j42.6−j2Z0cotπ/2になります。
ところで、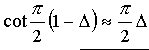 です。ちゃんと考えると、上の式の赤い部分が(π/2)-Δになるんでしょうけど、なってません。それはそれ、cotπ/2の部分を(π/2)Δに置き換えます。
です。ちゃんと考えると、上の式の赤い部分が(π/2)-Δになるんでしょうけど、なってません。それはそれ、cotπ/2の部分を(π/2)Δに置き換えます。
すると、Zab≒73.1+j42.6−j2Z0(π/2)Δ となります。
あとは虚数部分がなくなるように計算するだけですので、
42.6 = 2Z0(π/2)Δ
Z0 = 420[Ω] (と問題に書いてある)ので、これを代入して
Δ = 0.032
答えは3.2%です。
ちなみに位相定数のこととかを知らなくても、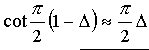 と与えられている時点で「ああ、cotのところを(π/2)Δに置き換えるのね」と考えるのが筋なので、なにも考えなくてもZab≒73.1+j42.6−j2Z0(π/2)Δとします、私は。
と与えられている時点で「ああ、cotのところを(π/2)Δに置き換えるのね」と考えるのが筋なので、なにも考えなくてもZab≒73.1+j42.6−j2Z0(π/2)Δとします、私は。
平成12年7月 1陸技 無線工学BのB-4
次の記述は、図に示すナイフエッジの形をした山頂の点Cにおける回折損を誘導する過程について述べたものである。□内に入れるべき字句を下の番号から選べ。ただし、□内の同じ記号は同じ字句を示す。また、大地の反射係数は-1とし、距離d
1[m]及びd
2[m]は、高さh
0、h
1及びh
2に比べて十分大きいものとする。
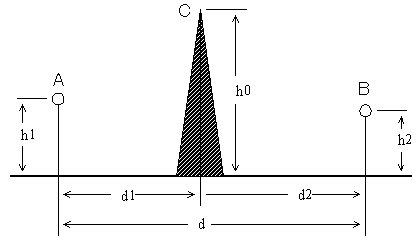
(1) 送受信点間にナイフエッジが無い場合、自由空間の電界強度をE
0[V/m]とすれば、B点における地上波電界強度E
dは、次式で与えられる。
E
d=□ア×sin(2πh
1h
2/λd)[V/m] …○1
(2) ナイフエッジがある場合の回折損をSとすれば、B点における電界強度Eは、次式となる。
E
d=□イ×sin(2πh
1h
0/λd
1)×sin□ウ[V/m] …○2
(3) h
1を上下に変化させてEが最大になったときには、次式となり、
sin(2πh
1h
0/λd
1)=□エ …○3
h
2を変化させてEが最大になったときには、次式となる。
sin(ウ)=□エ …○4
(4) したがって、○2、○3及び○4式より、回折損Sは次式で示される。
S=□オ
1 2E
0 2 4E
0S
3 sin(2πh
2h
0/λd
2)
4 E
0 5 E
0S
6 1
7 E/4E
0 8 sin(2πh
1h
2/λd
2)
9 E/E
0 10 1/2
- 直接波と大地反射波の合成電界
- 直接波と大地反射波の合成電界
まず解答のグループわけです。
1と4、2と5、3と8、6と10、7と9が対です。
□アですが、知らなきゃ分かりません。また、ここで間違えると後の選択肢の大部分を間違えます。答えは1です。この式は暗記してください。
□イですが、「回折損をSとすれば」なのでSが入っているものを選びます。単純に考えると、□アで4を選んだ方用に5の解答を作って、□アで1を選んだ方用に2の解答を作っている気がします。したがって、2を選びます。こんな説明で納得いくか、と思う方は自分で勉強してくださいと言いたいところですが、簡単なので説明します。
まず、下の図の黒丸の所の合成受信電界強度を求めます。
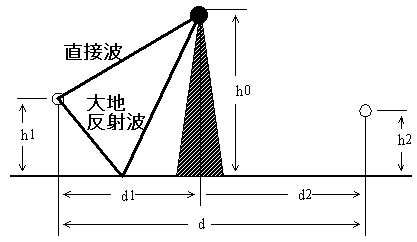
送信アンテナの高さがh1[m]、黒丸の高さがh0[m]、距離はd1[m]なので黒丸の点の電界強度は2E0×sin(2πh1h0/λd1)[V/m]。
次に黒丸のところから、受信アンテナのところまで電波が飛びます。黒丸のところから出る電波の強度は2E0×sin(2πh1h0/λd1)[V/m]に回折損Sをかけて、2E0S×sin(2πh1h0/λd1)[V/m]になります。これをE0'としましょう。
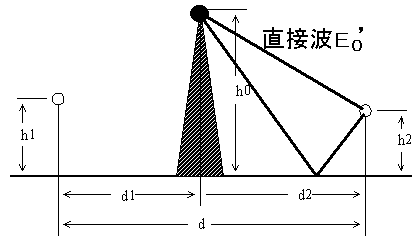
黒丸の高さがh0[m]、受信アンテナの高さがh2[m]、距離はd2[m]なので受信アンテナの電界強度は2E0'×sin(2πh0h2/λd2)[V/m]。ここで、E0'=2E0S×sin(2πh1h0/λd1)なので、受信アンテナの電界強度は4E0S×sin(2πh1h0/λd1)×sin(2πh0h2/λd2)
□ウですが、上に答え書いてしまったんですけど、Ed=□イ×sin(2πh1h0/λd)×sin□ウ[V/m]で、最初のsinの項はh1からh0のことを指しているので、□ウはh0からh2のことを指さないといけないです。したがって答えは3です。
やっと□エです。三角関数を使うのはこれだけです。h1を上下に変化させるということはsinの値が上下するってことです、sinの値は1〜-1の値をとります。sinが1をとった時にEが最大になります(よね、-1より1の方が大きいですよね)。したがって、□エは6です。
□オですが、○2の式でsinの値が1の時はE=4E0Sになります。したがって、S = E / 4E0です、答えは7です。
平成12年7月 2陸技 無線工学BのA-4
 周波数30[MHz]で使用する半波長ダイポールアンテナの実効長として、最も近いものを下の番号から選べ。
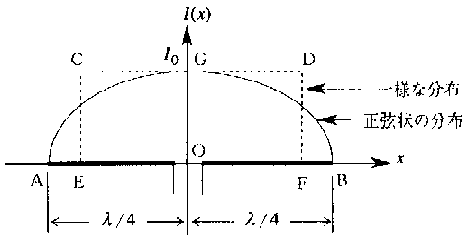
周波数30[MHz]で使用する半波長ダイポールアンテナの実効長として、最も近いものを下の番号から選べ。ただし、図に示すように、アンテナの中心Oを原点にとり、アンテナ素子の長さ方向をx[m]とし、アンテナの給電点電流I
0[A]及び波長をλ[m]としたとき、電流分布は次式で表される正弦状の分布とする。また、正弦状の電流分布の面積AGBに等しい面積CDFEを持ち、かつ、給電点電流が等しい一様な電流分布を考えたとき、長さEFを実効長l
e[m]という。
I(x)=I
0cos(2πx / λ)
1 0.8[m]
2 1.6[m]
3 2.2[m]
4 2.8[m]
5 3.2[m]
問題の意図がさっぱりわかんないです。これ、4アマの問題です。実効長を導出する過程を示せと言われたら2陸技の問題。こういう問題の出し方だと4アマの問題。
三角関数は出てきていますが、使いません。問題文の赤い部分だけを読みます。半波長ダイポールアンテナの実効長はλ/πです。これは無線屋さんには常識です。
λ = 3.0×108/周波数 = 3.0×108 / 30×106 = 10[m]
実効長 = λ/π = 10 / 3.14 = 3.2[m]
よって答えは5です。実効長の意味を知りたい方はアンテナ工学の初歩なんで適当な本を読んでください。試験に受かるためには実効長を丸暗記した方が1000倍くらい早いでしょう。
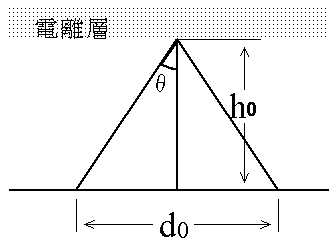
電離層の臨界周波数が4[MHz]で見かけの高さが300[km]のとき、周波数5[MHz]の電波の跳躍距離の値として正しいものを下の番号から選べ。ただし、大地は水平な平面であり、電離層は大地に平行であるものとする。図は、電離層の見かけの高さがh
0[m]であり、電離層への電波の入射角がθ度のとき、電離層反射波が届く地表距離d
0[m]を示したものである。また、臨界周波数f
c[Hz]と周波数f
0[Hz]との間には、次式の関係があるものとする。
f
0 = f
csecθ
1 450[km]
2 600[km]
3 900[km]
4 1200[km]
5 1800[km]
さすが2陸技。式が与えられてるぜ、という感じです。d0を求めます。
secθ= 1/cosθです。無線の試験を受けるならば覚えておくべきでしょう。
f0 = fcsecθ これに臨界周波数fc= 4[MHz]、周波数f0 = 5[MHz]を代入します。
5 = 4 secθ
secθ = 1.25
cosθ = 1/1.25 = 0.8
ここで
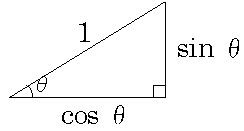 なので、これを問題の図にあてはめてみます。cosθは0.8なので
なので、これを問題の図にあてはめてみます。cosθは0.8なので
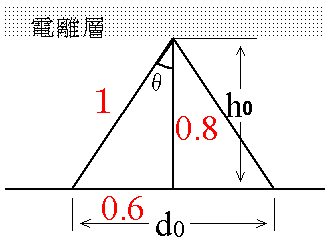
となります。sinθの方は0.6になります。なんで0.6になるかといいますと、この三角形は3:4:5の三角形になっているからです。8という数字を見たら怪しいと思ってください。100発100中で3:4:5の三角形になっているはずです。
したがって、
h0 : 0.8 = d0/2 : 0.6 h0は問題に与えられているので
300 : 0.8 = d0/2 : 0.6
d0 = 450
したがって、答えは1です。
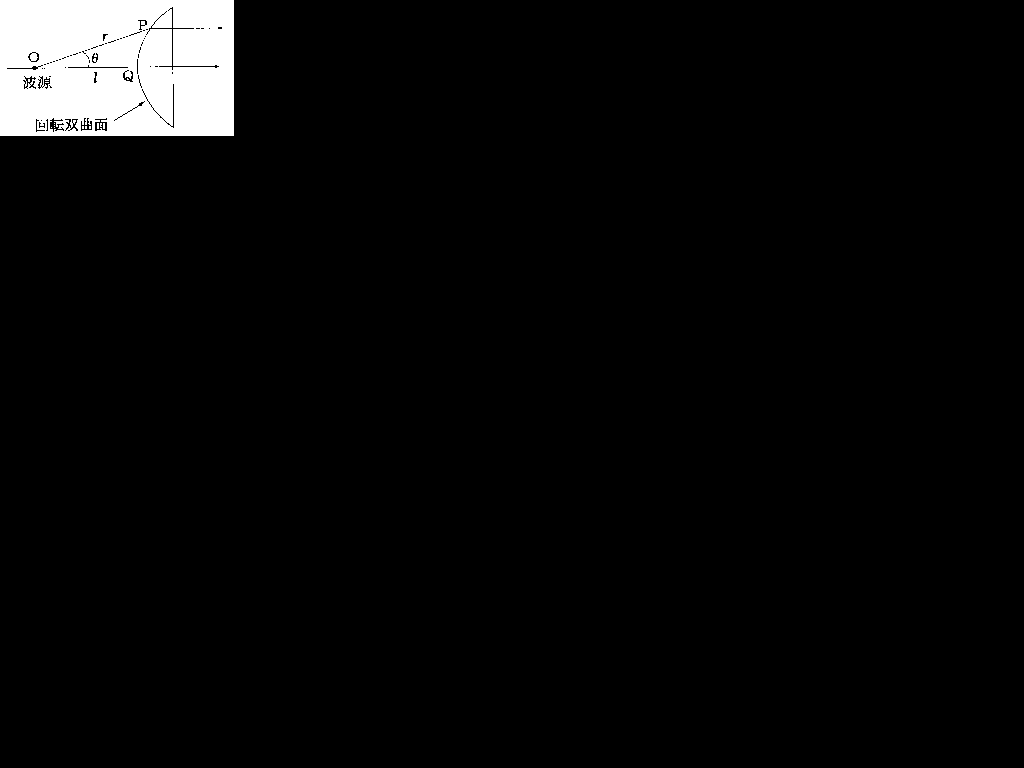
A-10 図に示す誘電体レンズアンテナにおいて、レンズの軸上の波源Oから回転双曲面上の任意の点Pまでの距離をr、Oから軸と回転双曲面との交点Qまでの距離をl、角POQをθ及び誘電体の屈折率をnとしたとき、rを表す式として、正しいものを下の番号から選べ。
 1
1 r=l/(n cosθ-1)
2 r=(n-1)l/(n cosθ-1)
3 r=l/(1-n sinθ)
4 r=nl/(1-n sinθ)
5 (n-1)l/(1-n sinθ)
こういう問題は分かりやすい点で考えるのが基本です。以下にやり方を示します。
まず、θが0の時を考えてみます。θが0だとsinθは0、cosθは1です。以下の図のようになります。
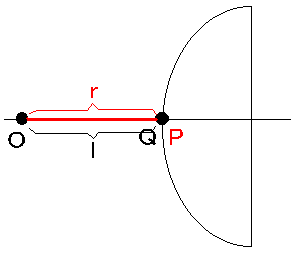
図から分かるようにr = lです。したがって、sinθ=0、cosθ=1の時にr = lとなるような式を選択肢から選ぶと、2か3です。
次に2と3、どちらを選ぶかということです。cosθとsinθの違いです。ここまでくると感覚でしかないのですが、私は以下のように考えます。
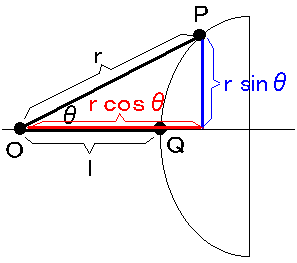
この図をぱっと見てcosθとsinθどちらを選びますか? lをどんなにいじくっても、r sinθと同じにはなりそうにもないですよね。したがってcosθの方を選びます。
ちなみに本当の理論は私は知りません(ぉい
B-3 次の記述は、ターンスタイルアンテナについて述べたものである。□内に入れるべき字句を下の番号から選べ。ただし、図に示すように、半波長ダイポールアンテナからθ方向の一定距離の点Pにおける電界強度eは、アンテナに流れる電流の最大値Iを、角周波数をω及び定数をkとすれば、次式で表されるものとする。
e=kIsinωtsinθ

(1) 二つの半波長ダイポールアンテナを中心で直交して互いに□ア度の位相差をもつ振幅の等しい電流で砺振し、二つの半波長ダイポールアンテナを含む面を水平にして水平方向の□イ偏波の電波を放射する。
(2) 直交した二つの半波長ダイポールアンテナを含む平面上の点Pにおける合成電界の強度e
tは、それぞれのアンテナの電界強度をe
1及びe
2とすれば次式となる。
e
t=e
1+e
2
=kIsinωsinθ+□ウ
=kI(sinωtsinθ+cosωtcosθ)
=kIcos(ωt-θ)
(3) 上式より、合成電界の最大値の方向は角速度ωで回転し、電界の最大振幅kIは、二つの半波長ダイポールアンテナを含む平面上で一定であるので、指向性は水平面でほぼ□エとなる。
(4) 利得を増加するには、このターンスタイルアンテナを垂直方向に必要な段数を重ねて配置し、格段を□オで砺振する。
1 90
2 単一指向性
3 水平
4 180
5 kIsin(ωt+π/4)sin(π/4-θ)
6 垂直
7 同相
8 無指向性
9 逆相
10 kIsin(ωt+π/2)sin(π/2-θ)
いかにも難しそうな式が出ていますがおそるるに足りません。無線の試験で出てくる角度はほとんど90度、ラジアンで言えばπ/2です。
まずグループわけです。陸技の問題は解答が2つ一組になっています。で、どちらかが答えです。したがって、最初に解答をグループ分けするのは重要です。
「90、180」「単一指向性、無指向性」「水平、垂直」「kIsin(ωt+π/4)sin(π/4-θ)、kIsin(ωt+π/2)sin(π/2-θ)」「同相、逆相」
□アですが、角度を聞かれたら90度です。よってアは90です。
□イですが、水平にしたら水平偏波しかでるわけないです。よって、イは水平です。
□ウですが、式の違いはπ/2かπ/4かです。□アで90度を選んでいます。e1とe2ではなにかが90度違う、90度はラジアンでいうと、π/2です。したがってπ/2を選ぶのが妥当です。よって、ウはπ/2のほうです。
□エですが、「最大振幅は平面上で一定」とあるので、無指向性に決まってます。よってエは無指向性です。
□オですが、格段を逆相で砺振したら打ち消しあってしまうので同相に決まってます。逆相で砺振することはないです。したがって□オは同相です。
ア:1 イ:3 ウ:10 エ:8 オ:7
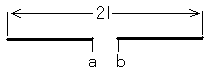 図に示す長さが2l[m]の半波長ダイポールアンテナの特性インピーダンスが420[Ω]であるとき、給電点abから見たインピーダンスを純抵抗とするためのアンテナ素子の短縮率として、最も近いものを下の番号から選べ。ただし、位相定数をβ[rad/m]とすれば、長さ2lで特性インピーダンスZ0[Ω]のアンテナのab端子から見たインピーダンスZabは、次式で与えられるものとする。
図に示す長さが2l[m]の半波長ダイポールアンテナの特性インピーダンスが420[Ω]であるとき、給電点abから見たインピーダンスを純抵抗とするためのアンテナ素子の短縮率として、最も近いものを下の番号から選べ。ただし、位相定数をβ[rad/m]とすれば、長さ2lで特性インピーダンスZ0[Ω]のアンテナのab端子から見たインピーダンスZabは、次式で与えられるものとする。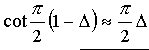
 (1) 送受信点間にナイフエッジが無い場合、自由空間の電界強度をE0[V/m]とすれば、B点における地上波電界強度Edは、次式で与えられる。
(1) 送受信点間にナイフエッジが無い場合、自由空間の電界強度をE0[V/m]とすれば、B点における地上波電界強度Edは、次式で与えられる。


 電離層の臨界周波数が4[MHz]で見かけの高さが300[km]のとき、周波数5[MHz]の電波の跳躍距離の値として正しいものを下の番号から選べ。ただし、大地は水平な平面であり、電離層は大地に平行であるものとする。図は、電離層の見かけの高さがh0[m]であり、電離層への電波の入射角がθ度のとき、電離層反射波が届く地表距離d0[m]を示したものである。また、臨界周波数fc[Hz]と周波数f0[Hz]との間には、次式の関係があるものとする。
電離層の臨界周波数が4[MHz]で見かけの高さが300[km]のとき、周波数5[MHz]の電波の跳躍距離の値として正しいものを下の番号から選べ。ただし、大地は水平な平面であり、電離層は大地に平行であるものとする。図は、電離層の見かけの高さがh0[m]であり、電離層への電波の入射角がθ度のとき、電離層反射波が届く地表距離d0[m]を示したものである。また、臨界周波数fc[Hz]と周波数f0[Hz]との間には、次式の関係があるものとする。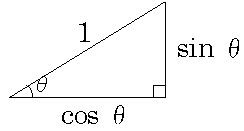 なので、これを問題の図にあてはめてみます。cosθは0.8なので
なので、これを問題の図にあてはめてみます。cosθは0.8なので



