図において、電気通信回線への入力電圧が120mV、その伝送損失が1kmあたり1.2dBの時、電圧計の読みが16mVでした。増幅器の利得は何dBでしょう。ただし、変成器は理想的なものとし、電気通信回線及び増幅器の入出力インピーダンスはすべて同一値で、各部は整合しているものとします。
ここにある文書の作成にあたってsumito様にとてもお世話になりました。
持っていませんでしたら関数電卓買ってください。合格体験記なんかで、本番に備えて一週間前には手計算でやりましょう、とかありますけど、手で計算してる暇あったら関数電卓叩いて問題を解いていた方がよっぽど勉強になると思うのは私だけですか?
「雑学」と書いてある項目は雑学です。知っていると納得したり実務で役にたったりしますが、資格試験には出ません。
特に無線の世界ではなんでもかんでもデシベルであらわします。なんでかと言うとデシベルで計算すると足し算と引き算ですべてが済むからです。
例えば、地球局から衛星に10[GHz]で3[kW]の電波を飛ばしたとします(アンテナ利得は0としましょう)。衛星に電波がたどり着いた時には自由空間伝搬損失のため1/(2.2×1020)倍になって、1.3×10-17 [W]になります。
ここで昔の人はこう思いました。1.3×10-17 [W]ってどのくらいの出力なのよ?
また、こうも思います。1/(2.2×1020)倍するのって関数電卓でもなきゃ出来ないじゃん
そこで、真数をデシベルに換算して計算することにしました。3[kW](真数)は34.77[dBW](デシベル)、2.2×1020(真数)は203.42[dB](デシベル)です([dBW]と[dB]の違いは後述します)。衛星に電波がたどり着いた時には、34.77[dBW] - 203.52[dB] = -168.75[dBW]。-168.75[dBW]を真数にすると、1.3×10-17 [W]となります。換算に手間がかかりますが計算自体は足し算と引き算で計算出来てお得です。
今の計算では最後に真数に直しましたけど、普通はデシベルのまま扱います。受信レベルは -168.75[dBW] というような感じです。真数は、最初の出力にしか使用しないです。
ここで理解して頂きたいのは、デシベルの方が慣れると分かりやすいということだけです。
ここの内容は楽々マークシート試験と同じ・・・のはずだったんですが、足りない部分があったので多少補いました。
まず覚えてください。「log」は「ろぐ」と読みます。「log2」は「ろぐに」です。
log2=0.3
log3=0.477
log5=0.7
log10=1
次にlogの後についている数字の指数はlogの前に出すことが出来ます。実例見れば分かります。
log102=2log10=2×1=2
log103=3log10=3×1=3
log10x=xlog10=x×1=x
log4=log22=2log2=2×0.3=0.6
log8=log23=3log2=3×0.3=0.9
さらに以下の公式を覚えてください。
log(A×B)=logA+logB
例 log6=log(2×3)=log2+log3=0.3+0.477=0.777
log(A÷B)=logA−logB
例 log5=log(10÷2)=log10−log2=1−0.3=0.7
ここまでは、logの数字を普通の数(真数といいます)になおしました。その反対はどうやるかです。
0.3=log2
0.477=log3
1=log10
x=log10x
これは暗記事項です。
ここからは実例見て学んでください。意味を説明するのめんどいんで(ぉい
1.477=1+0.477 1はlog10です。0.477はlog3です。 ここで10と3をかけて10×3=30です。
よって、1.47=log30です。
3.3=3+0.3 3はlog103です。0.3はlog2です。 ここで103と2をかけて103×2=2×103です。
よって、3.3=log(2×103)です。
最初の分解は、整数部分とそれ以外に分ければそれでおっけです。
単位によって真数とデシベルで表す数値の換算の仕方が違います。
G'[dB]=10logG(真数) G[単位なし] 利得です
P'[dB]=10logP(真数) P[W] 電力です
E'[dB]=20logE(真数) E[V/m] 電界です
V'[dB]=20logV(真数) V[V] 電圧です
I'[dB]=20logI(真数) I[A] 電流です
下の例題でEとVの扱いが適当になってるところがありますが、式は同じなので勘弁してください。
X = logY の時
10X = Y
例
0.3=log2
100.3=2
関数電卓がないと計算不可能です。関数電卓を持っていたら試してください。
電界強度80[dB](1[μV/m]を基準とした値)の電界はいくつでしょう?
E[dB]=20logE(真数)
80[dB]=20logE[μV/m]
4[dB]=logE[μV/m]
4[dB]=log104[μV/m]
よってE=104[μV/m]=10-2[V/m]
陸技の試験にはdBとdBWとdBmの3種類の単位が出てきます。実務の世界ではこれにdBμを加えた4つの単位が出てきます。
dBはなんの断りもなければ相対利得を表します。
このアンプは30[dB]の利得があると言った場合、
30=10logG
3=logG
G=1000
となり、例えばアンプに1mWの信号を入れると、1000倍の1Wになって出てきます。2mWの信号を入れると、1000倍の2Wになって出てきます。
dBWとdBmとdBμは絶対利得を表します。dBWは1W=0dBW、dBmは1mW=0dBm、dBμは1μW=0dBμです。
例えば2WをdBWとdBmとdBμで表してみましょう。
dBWの場合
10log2=10×0.3=3[dBW]
dBmの場合(2[W]=2000[mW])
10log2000=10×log(2×103)=10×(log2+log103)=10×(0.3+3)=33[dBm]
dBμの場合(2[W]=2000000[μW])
10log2000000=10×log(2×106)=10×(log2+log106)=10×(0.3+6)=63[dBμ]
2Wの信号を利得30[dB]のアンプ(入力を1000倍にするアンプ)に入力すると、出力は2000Wになります。これをデシベルで計算してみましょう。
上で見たとおり、2Wは3[dBW]です。利得30[dB]のアンプに信号を入力すると、
3[dBW]+30[dB]=33[dBW]
33=10logP
3.3=logP
3+0.3=logP ここで0.3=log2、3=log103なので
P=2×103[W]
と確かに2000[W]になります。
次に単位が[dBm]でも同じ結果が得られるかどうかを調べてみましょう。
上で見たとおり、2Wは33[dBm]です。利得30[dB]のアンプに信号を入力すると、
33[dBm]+30[dB]=63[dBm]
63=10logP
6.3=logP
6+0.3=logP ここで0.3=log2、6=log106なので
P=2×106[mW]=2×103[W]
と確かに2000[W]になります。
単位が[dBμ]でも同じ結果が得られます。面倒なので例は勘弁してください。
10[dBm]+10[dBm]=13[dBm]です。なぜでしょうか? 考えてみましょう。真数に換算して見ればすぐに分かります。分からない方は掲示板でもメールにでも書いてください。
「電力が3dB増加する」と言った場合は
3=10logP
0.3=logP
P=2
より「電力が2倍になる」ということです。
では、「電力が3dB下がる」と言った場合はどうなるかというと、「1/2」になります。理屈を知りたい方は数学の教科書読んでください。
「電力が10dB増加する」と言った場合は
10=10logP
1=logP
P=10
より「電力が10倍になる」ことです。
「電力が10dB下がる」と言った場合は、電力は「1/10」になります。
分かって頂けたでしょうか?
今までの計算は関数電卓を叩かなくても計算出来ました。資格試験では関数電卓を叩かなくても計算出来るようになっているので当然ですが。でも、log5を計算するのにいちいちlog(10−2)を計算してるのはやってらんないので、計算方法を示します。
「log」と「5」を押すだけです。
0.6=logP という式は
100.6=P という式と同じです。
したがって、0.6=logPという式のPを知りたいときは、100.6を関数電卓で計算します。
携帯電話が0.35Wの出力で電波を出したとします。さて、何dBmでしょう?
0.35[W]は350[mW]です。したがって、
10log350
=25.44[dBm]
関数電卓を叩かないと計算不可能です。多分。
測定に使うケーブルの損失が0.35dBと分かりました。さて、信号はどのくらい減衰するんでしょう?
0.35=10logP
0.035=logP
P=100.035
P=1.084
よって、信号を入れると出口では1/1.084倍になって出てきます。たとえば、1mWの信号をこのケーブルに通すと、0.92mWになって出てきます。
我々がいつも測定に使っているたった1mほどのケーブルなんですが、はじめて真数を計算してみたんですけど、結構馬鹿にならないですね・・・。
3dBmとは上で説明したとおり、
3=10logP
0.3=logP
P=2[mW]です。では、−3dBmっていうのは何mWでしょう?
−3=10logP
−0.3=logP
P=10−0.3 関数電卓を叩いてください。
P=0.5[mW]です。
3dBmというのは、1mWの2倍で2mWです。
−3dBmというのは、1mWの1/2で0.5mWです。
−10dBmは何mWと聞かれたら、10dBmは1mWの10倍で10mWなので、−10dBmは1mWの1/10で0.1mWです。
次の電力をデシベル(dBW)に換算しましょう。
(1) 4[kW]
(2) 100[kW]
(3) 3[kW]
(1) 10log(4×103[W])=10(log4+log103)=10(log22+log103)=10(2×log2+3×log10)=10(2×0.3+3×1)=36[dBW]
(2) 10log(105[W])=10(5×log10)=10(5×1)=50[dBW]
(3) 10log(3×103[W])=10(log3+log103)=10(0.477+3)=34.77[dBW]
例題1
周波数6,000[MHz]の電波を用いて衛星直下の地球局から静止衛星に送信するとき、衛星の受信機入力の値は何dBWか。ただし、衛星局受信フィーダ損は無視出来るものとし、衛星受信アンテナの利得を17.0[dB]、地球局送信アンテナ利得を63.0[dB]、地球局送信フィーダ損を0.4[dB]、地球局送信機出力を4[kW]、静止衛星までの高さを35,900[km]、log3=0.4771とする。
デシベルで計算する場合、
送信出力+利得−損失=受信機入力
となります。
まず、送信出力をデシベルに換算します。
10log4×103=10(log22+log103)=10(2log2+3log10)=10(2×0.3+3×1)=36[dBW]
次に自由空間伝搬損失を求めます。自由空間伝搬損失Γは真数なので、デシベルに直さないと駄目です。dは単位が[m]なので、気をつけましょう。(周波数から波長の求め方)
10logΓ
=10log(4πd/λ)2 ここで2を前に出してしまいます。
=20log(4π×35,900×103÷0.05)
=20log(9.0×109)
=20log32+20log109
=40log3+180log10
=40×0.4771+180×1
=199.084[dB]
あとは、送信出力+利得−損失=受信機入力で計算するだけです。
地球局送信機出力+衛星受信アンテナの利得+地球局送信アンテナ利得−地球局送信フィーダ損−自由空間伝搬損失=衛星の受信機入力
36+17+63−0.4−199.084=−83.484[dBW]
ちなみに、−83.484[dBW]=4.48×10-9[W]です。
例題2
周波数4[GHz]、送受信点間距離5[km]、送信電力100[kW]、送信アンテナ利得30[dB]、最少受信入力レベル22[dBm]の見通し回線がある。自由空間伝搬損失L[dB]、受信アンテナ利得Gr[dB]及び受信アンテナ実効面積Ae[m2]の値を求めよ。ただし、log7=0.845とする。
まず距離と波長が分かっているので、自由空間伝搬損失を求めます。
λ=3×108/4×109=0.075[m] (周波数から波長の求め方)
10logΓ
=10log(4πd/λ)2
=10log(4π×5×103÷0.075)2 例題1みたいに2を前に出して20logの形にしてしまうと、log7=0.845を利用できないので前に出さないで計算します。
=10log(7.0×1011)
=10log7+10log1011
=10log7+110log10
=10×0.845+110×1
=118.45[dB]
次に受信アンテナ利得Grを求めます。とりあえず、送信出力をデシベルに換算します。最小受信入力レベルの単位が[dBm]となっているので、単位を[dBm]にあわせます。
送信出力は100[kW]=108[mW]
10log108=80log10=80[dBm]
送信出力+利得−損失=受信機入力より
送信出力+送信アンテナ利得+受信アンテナ利得−自由空間伝搬損失=最小受信入力レベル
80+30+Gr−118.45=22
Gr=30.45[dB]
最後におまけですが、アンテナ実効面積Aeを求めます。
アンテナの実効面積を求める公式の利得Gは真数なのでデシベルを真数に直します。
受信アンテナ利得は30.45[dB]なので、約30[dB]です。これを真数に直すと
30=10logG
3=logG
G=1000 (log103=3log10=3×1=3 ですね)
後はAe=λ2G/4πの公式に入れるだけです。
Ae
=(0.075)2×1000÷4π
=0.448[m2]
例題3
開口面積が10[m2]、絶対利得が40[dB]のアンテナを、3[GHz]の電波で使用した場合の開口効率(利得係数)の値はいくつでしょう。
アンテナの実効面積Aeの求め方、実効面積と開口面積
Ae=λ2G/4π
Ae=ηA
この2つの式より、η(開口効率)=λ2G/4πA
この式のGは真数なのでデシベルを真数に直します。
40=10logG
4=logG
G=10000 (log104=4log10=4×1=4 ですね)
波長は0.1mですね。
η
=λ2G/4πA
=(0.1)2×10000/(4π×10)
=0.796
例題4
周波数10[GHz]の電波を用いて衛星直下の地球局から静止衛星に送信するとき、衛星の受信機入力の値は何dBWか。ただし、衛星局受信フィーダ損は無視出来るものとし、衛星受信アンテナの利得を15.0[dB]、地球局送信アンテナ利得を61.0[dB]、地球局送信フィーダ損を0.8[dB]、地球局送信機出力を3[kW]、静止衛星までの高さを35,900[km]、log3=0.4771とする。
送信出力+利得−損失=受信機入力
まず、送信出力をデシベルに換算します。
10log(3×103)=10(log3+log103)=10(log3+3log10)=10(0.477+3)=34.77[dBW]
次に自由空間伝搬損失を求めます。自由空間伝搬損失Γは真数なので、デシベルに直さないと駄目です。dは単位が[m]なので、気をつけましょう。(周波数から波長の求め方)
10logΓ
=10log(4πd/λ)2 ここで2を前に出してしまいます。
=20log(4π×35,900×103÷0.03)
=20log(15×109)
=20log(3×5)+20log109
=20log(3×10÷2)+180log10 log5がわからないので、log(10/2)とします。これはlog10とlog2は分かるからです。
=20log3+20log10−20log2+180log10 注 log(A/B)=logA−logBです。
=20×0.4771+20×1−20×0.3+180×1
=203.542[dB]
あとは、送信出力+利得−損失=受信機入力で計算するだけです。
地球局送信機出力+衛星受信アンテナの利得+地球局送信アンテナ利得−地球局送信フィーダ損−自由空間伝搬損失=衛星の受信機入力
34.77+15+61−0.8−203.54=−93.57[dBW]
ちなみに、−93.57[dBW]=4.4×10-10[W]です。
例題5
開口面積が2[m2]のアンテナの周波数3[GHz]における指向性利得が33[dB]である。このアンテナの開口効率はいくつでしょう。
アンテナの実効面積Aeの求め方、実効面積と開口面積
このGってのは絶対利得です。指向性利得じゃないです。でも、電波受験界を見るとなんか絶対利得として計算してます。なんででしょうか。しかしそこで疑問に思わず「まあ、そんなもんなんだな」と納得するのが早いです。こんなこといちいち疑問に思っていたら日がくれます。
今回は開口効率ηが知りたいので、「η=」の式になおして計算するだけです。
η=λ2G/4πA
周波数3[GHz]は波長に直すと0.1[m](波長と周波数の換算)。
利得33[dB]を真数に直すと
33=10log x
3.3=log x
3+0.3=log x
3はlog103で0.3はlog2なので、103×2で、2×103。従ってGは2×103。
πは3.14で計算。
η=λ2G/4πA
η=0.12×2×103/4×3.14×2
η=0.8
例題6
周波数10[GHz]の電波を用いて地球局から静止衛星の人工衛星へ送信し、人口衛星局の受信機入力を-90[dBW]以上にするために必要な地球局の最低送信機出力電力は何[dBW]でしょう。ただし地球局及び人口衛星局のアンテナの絶対利得を、それぞれ59[dB]及び20[dB]とし、給電系の損失及び大気による伝搬損失を無視するものとする。また、静止衛星と地球局との距離を36,000[km]とする。
まず自由空間伝搬損失Γを求めます。その前に波長を求めます(波長と周波数の換算)。
λ
=3.0×108/10×109
=0.03[m]
Γ
=10log(4πd/λ)2 ここで2を前に出してしまいます。
=20log(4π×36000×103÷0.03) dは単位が[m]なので、36000[km]は36000×103[m]です。今更ですが書いておきます。
=20log(15×109)
=20log(3×5)+20log109
=20log(3×10÷2)+180log10 log5がわからないので、log(10/2)とします。これはlog10とlog2は分かるからです。
=20log3+20log10−20log2+180log10 注 log(A/B)=logA−logBです。
=20×0.477+20×1−20×0.3+180×1
=203.54[dB]
あとは、送信出力+利得−損失=受信機入力で計算するだけです。
地球局送信機出力+地球局アンテナの利得+人口衛星局アンテナの利得−自由空間伝搬損失=人口衛星局の受信機入力
地球局送信機出力+59+20−203.54=−90[dBW]
地球局送信機出力=34.54[dBW]
ちなみに34.54[dBW]は2844[W]です。関数電卓で103.454を計算してみましょう。
例題7
周波数7[GHz]の電波において、絶対利得40[dB]のアンテナ利得を得るためにはパラボナアンテナの開口面の直径を何メートルにすればよいか? ただし開口能率は50[%]とする。
とりあえず面積を求めましょう。
アンテナの実効面積Aeの求め方、実効面積と開口面積
Ae=λ2G/4π
Ae=ηA
なので、「A=」になおすと
A
=λ2G/4πη
波長λ=3×108/7×109=0.043[m]
絶対利得40[dB]を真数になおすと、
40=10logG
4=logG log10x=xlog10=x ですね。
G=104
元にもどって
A
=λ2G/4πη
=0.0432×104/(4π×0.5)
直径をD[m]とすると、A=(D/2)2πなので、
(D/2)2π=0.0432×104/(4π×0.5)
D2=0.0432×104×22/(4π×0.5×π)
D2=(0.043×100×2)2/2π2
D=0.043×100×2/21/2π
D=1.936[m]
無線の試験の場合、電卓が使えないので上の計算のように最後の最後まで計算しない?方がいい場合もあります。
例題1
次の記述で誤っているものはどれか。
1. 1[μV]を0[dB]とした場合、1[mV]の電圧は60[dB]である。
2. 1[μV/m]を0[dB]とした場合、0.5[mV/m]の電界強度は54[dB]である。
3. 出力電力が入力電力の300倍になる増幅回路の利得は27[dB]である。
4. 電圧比で最大値から6[dB]下がったところのレベルは最大値の1/2になる。
5. 1[μW]を0[dB]とした場合、1[W]は30[dB]である。
6. 1[μV/m]を0[dB]とした場合、5[mV/m]の電界強度は74[dB]である。
1.について
1[mV]は1[μV]の1000倍です。
E'[dB]=20logE(真数)なので、
E'[dB]
=20log1000
=20log103 3を前に出すと
=60log10 log10=1なので
=60[dB]
よって、1.はあっています。
2.について
0.5[mV/m]は1[μV/m]の500倍です。
E'[dB]=20logE(真数)なので、
E'[dB]
=20log500
=20log(103÷2) log(A÷B)=logA−logBなので
=20(log103−log2)
=20log103−20log2
=60−20×0.3
=54[dB]
よって、2.はあっています。
3.について
電力なので、P'[dB]=10logP(真数)の式を使います。
300倍ですから、Pに300を代入すると、
P'[dB]
=10log300
=10log(3×102) log(A×B)=logA+logBなので
=10log3+10log102
=10×0.4771+20
=24.771[dB]
よって3.は間違っています。
4.について
E'[dB]=20logE(真数)
6[dB]=20logE
0.3=logE
E=2
電圧が6dB増加すると電圧は2倍になります。逆に電圧が6dB減少すると1/2になります。
ちなみに、電圧が12dB増加すると電圧は4倍になります。逆に電圧が12dB減少すると1/4になります。
また、電圧が18dB増加すると電圧は8倍になります。逆に電圧が18dB減少すると1/8になります。
よって4.はあっています。
5.について
1[W]は1[μW]の106倍です。
P'[dB]=10logP(真数)より
P'[dB]
=10log106
=60log10
=60[dB]
よって5.は間違っています。
6.について
5[mV/m]は1[μV/m]の5×103倍です。
E'[dB]=20logE(真数)より
E'[dB]
=20log(5×103)
=20log(104÷2)
=20log(104)−20log2
=80−20×0.3
=74[dB]
よって6.はあっています。
例題1
ある通信回線において、送信機出力が1[W]、送信及び受信アンテナの利得が各々14[dB]、送信及び受信給電線損失が各々2[dB]、自由空間伝搬損失が142[dB]の場合、受信機の入力電力は何[dBm]でしょう。
まず、送信機出力を[dBm]に直します。単位に注意します。送信機出力が1[W]なので、[mW]に直すと1000[mW]です。これをdBmに直します。P'[dB]=10logP(真数)より
P[dBm]
=10logP
=10log1000
=10log103 3を前に出して
=30log10
=30[dBm]
あとは、利得は足して損失は引くだけです。
送信機出力+送信アンテナの利得+受信アンテナの利得−送信給電線損失−受信給電線損失−自由空間伝搬損失=受信機の入力電力
30+14+14−2−2−142=−88[dBm]
例題1
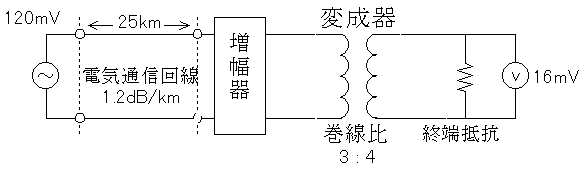
図において、電気通信回線への入力電圧が120mV、その伝送損失が1kmあたり1.2dBの時、電圧計の読みが16mVでした。増幅器の利得は何dBでしょう。ただし、変成器は理想的なものとし、電気通信回線及び増幅器の入出力インピーダンスはすべて同一値で、各部は整合しているものとします。

まず、変成器の左側の電圧を求めます。説明は省きますが、3 : 4 = x : 16mV よりx = 12mV です。すると以下の図のようになります。
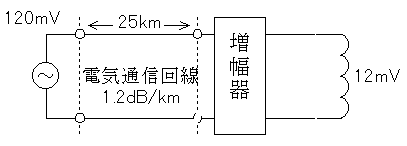
電気通信回路の損失は 1.2dB/km なので、25kmですと 25[km]×1.2[dB/km]=30[dB]
また入力電圧が120mVで出力は12mVになっているので、1/10になっています。
V'[dB]=20logV(真数)より電圧が1/10倍になると
V'[dB]
=20log10−1 −1を前に出して(注 1/10のことを10−1と書きます。ちなみに1/100のことは10−2と書きます。)
=−1×20log10
=−1×20
=−20[dB]
以上のことを整理すると以下の図のようになります。
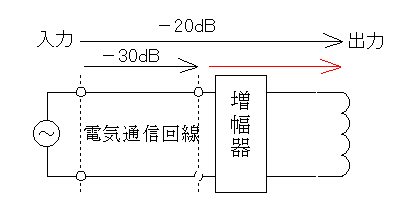
なんで30[dB]がマイナスになってんの?と思うかもしれないですが、損失ですのでマイナスです。損失だったらマイナス、利得だったらプラスです。
上の図から増幅器の利得は10[dB]ないと駄目だと分かります。
まず、変成器の左側の電圧を求めます。説明は省きますが、3 : 4 = x : 16mV よりx = 12mV です。すると以下の図のようになります。

電気通信回路の損失は 1.2dB/km なので、25kmですと 25[km]×1.2[dB/km]=30[dB]
ここまではやり方1と同じです
入力電圧と出力電圧を[dB]になおします。
V'[dB]=20logV(真数)より120mVは
V'[dB]
=20log120
=20log(22×3×10)
=20(log22+log3+log10)
=20(2log2+log3+log10)
=20(2×0.3+0.477+1)
=41.54
同様にして12mVは
V'[dB]
=20log120
=20log(22×3)
=20(log22+log3)
=20(2log2+log3)
=20(2×0.3+0.477)
=21.54
以上のことを整理すると以下の図のようになります。
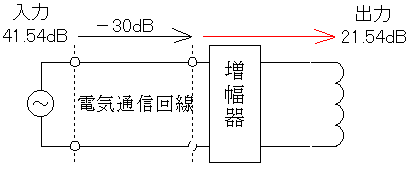
よって赤い部分は10[dB]ないと駄目です。
例題2
図において、電気通信回線への入力電流が12mA、増幅器の利得が24dBの時、電流計の読みが36mAでした。電気通信回線の損失は何dB/km(1kmあたりの損失)でしょう。ただし、変成器は理想的なものとし、電気通信回線及び増幅器の入出力インピーダンスはすべて同一値で、各部は整合しているものとします。
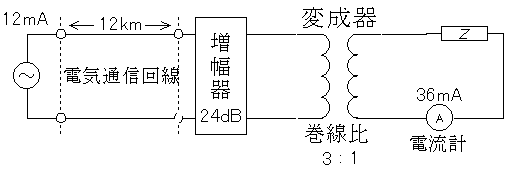
まず、変成器の左側の電流を求めます。説明は省きますが、1 : 3 = x : 36mA よりx = 12mA です。すると以下の図のようになります。
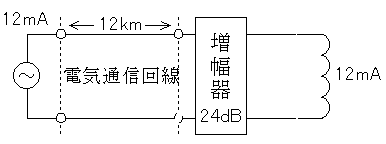
入力と出力が同じです。増幅器で24dBあがるので、電気通信回路で24dB下がっていればOKですね。
電気通信回線は12kmなので、24[dB]/12[km]=2[dB/km]となります。
例題3
図において、伝送損失が1kmあたり1.2dB、減衰器の減衰量が8dBの時、電圧計の読みが24mVでした。入力電圧は何mVでしょう。ただし、変成器は理想的なものとし、電気通信回線及び増幅器の入出力インピーダンスはすべて同一値で、各部は整合しているものとします。
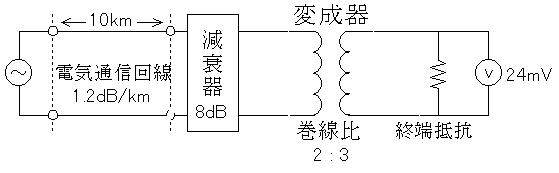
まず、変成器の左側の電圧を求めます。説明は省きますが、2 : 3 = x : 24mV よりx = 16mV です。
電気通信回路の損失は 1.2dB/km なので、10kmですと 10[km]×1.2[dB/km]=12[dB]
すると以下の図のようになります。
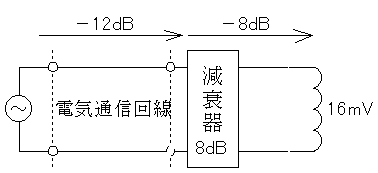
減衰器というのは、増幅器の反対の機能をもつもので、信号を弱くします。上の図より、合計で20dB下がります。
V'[dB]=20logV(真数)より
20=20logV
1=logV
V=10
したがって、入力に対して出力は1/10になります。出力が16mVなので、入力はその10倍の160mVです。
例題4
図において、電気通信回線への入力電圧が120mV、伝送損失が1kmあたり1.0dBの時、電圧計の読みが16mVでした。増幅器の利得は何dBでしょう。ただし、変成器は理想的なものとし、電気通信回線及び増幅器の入出力インピーダンスはすべて同一値で、各部は整合しているものとします。
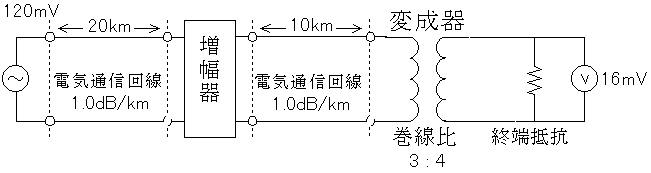
まず変成器の左側の電圧を求めます。説明は省きますが、3 : 4 = x : 16mV よりx = 12mV です。
また増幅器の左側の電気通信回線の損失は1.0[dB/km]×20[km]=20.0[dB]、増幅器の右側の電気通信回線の損失は1.0[dB/km]×10[km]=10.0[dB]
以上を図にすると、
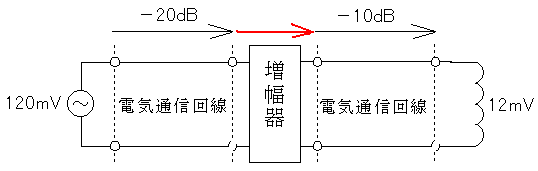
入力電圧が120mV、出力電圧が12mVなので、電圧は1/10になっています。したがってV'[dB]=20logV(真数)より
V[dB]
=20logV
=20log10−1 −1を前に出して
=−1×20log10
=−20[dB]
したがって下の図のようになります。
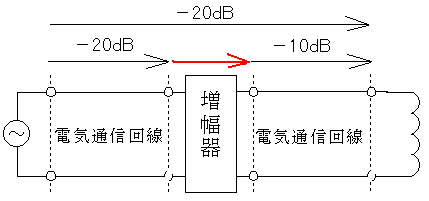
増幅器の利得は10dB必要です。
例題5
図において、電気通信回線1への入力電圧が180mV、電気通信回線1から電気通信回線2への遠端漏話減衰量が50dB、変成器の巻線比が図のように3:4だった時、電圧計の読みが24mVでした。増幅器の利得は何dBでしょう。ただし、変成器は理想的なものとし、電気通信回線及び増幅器の入出力インピーダンスはすべて同一値で、各部は整合しているものとします。
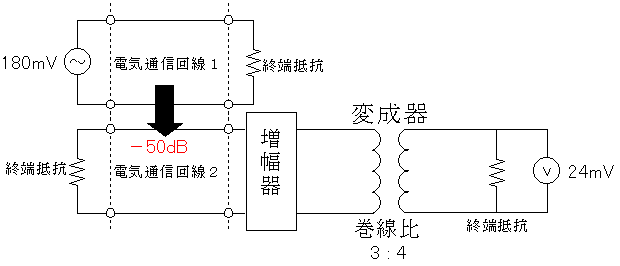
まず変成器の左側の電圧を求めます。説明は省きますが、3 : 4 = x : 24mV よりx = 18mV です。
次に遠端漏話というのは教科書を見て頂きたいのですがちょい説明します。一方の回線の信号が他の回線に漏れる現象を漏話といいまして、下の図の矢印の方向に漏れるのを遠端漏話、電気通信回線2の終端抵抗の方に漏れるのが近端漏話と言います。問題では遠端漏話しか出てこないと思います。
遠端漏話減衰量というのは、電気通信回線1に流れる電圧、電流、電力のうちどのくらい電気通信回線2に漏れるかというのを表したものです。減衰量が50dBなので、今の問題では入力電圧に対して50dB下がった電圧が電気通信回線2に出て来ちゃいます。
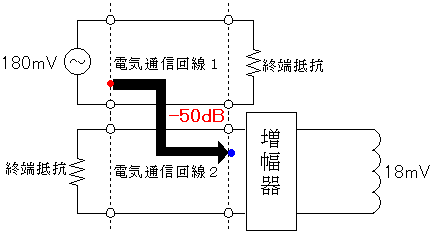
電気通信回線1の入力電圧が180mV、電気通信回線2の出力電圧が18mVなので、電圧は1/10になっています。したがってV'[dB]=20logV(真数)より
V[dB]
=20logV
=20log10−1 −1を前に出して
=−1×20log10
=−20[dB]
したがって下の図のようになります。
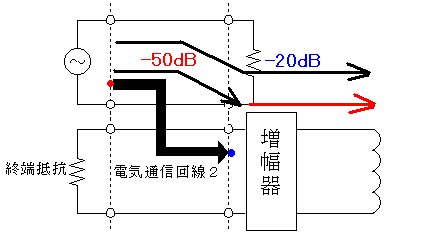
増幅器の利得は30dB必要です。
例題6
図において、A方向における漏話減衰量は何dBでしょう。ついでに、遠端漏話減衰量も求めましょう。さらに、発振器がついている方の回線の伝送損失も求めましょう。
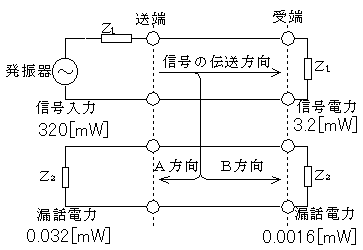
まずA方向における漏話減衰量です。
入力電力が320mW、A方向の漏話電力をみると0.032mWなので、電力は0.0001倍になっています。したがってP'[dB]=10logP(真数)より
P[dB]
=10logP
=10log10−4 −4を前に出して
=−4×10log10
=−40[dB]
答えは40dBです。なんで-40dBじゃないかというと減衰量が知りたいからです。40dB減衰するということは、電力が-40dBになるということです。
次に遠端漏話減衰量です。
入力電力が320mW、B方向の漏話電力をみると0.0016mWなので、電力は0.000005倍になっています。したがってP'[dB]=10logP(真数)より
P[dB]
=10logP
=10log(5×10−6)
=10log(10/2×10−6)
=10log(1/2×10-5)
=10log(2-1×10-5)
=10log2-1+10log10-5
=−10log2−50log10
=−10×0.3−50×1
=−53[dB]
答えは53dBです。
最後に発振器がついている方の回線の伝送損失です。
入力電力が320mW、信号電力をみると3.2mWなので、電力は0.01倍になっています。したがってP'[dB]=10logP(真数)より
P[dB]
=10logP
=10log10−2 −2を前に出して
=−2×10log10
=−20[dB]
答えは20dBです。