2001年8月9日
管理図
最初に
この文書は、電気通信主任技術者総合情報の掲示板のろくえもんさんの質問に対しての回答を記したものです。
自己レスを読んでなかなか楽しかったのと、管理工学科の血が騒いだのでなんとなく書きました。
ろくえもんさんのお役に立てると幸いです。
管理図ってなに?
細谷克也『やさしいQC手法演習 QC七つ道具』日科技連 1982によると管理図とは
工程における偶然要因による変動と異常原因による変動を区分して、工程を管理するために考案されたものであり、1本の中心線(CL)とその上下に合理的に決められた管理限界線(UCL、LCL)からなっている。
工程の状態をあらわす特性値がプロットされたとき、すべての点が上下2本の管理限界線内にあり、点の並び方にクセがなければ、工程は’管理状態にある’とみなすことができる。一方、点が限界外のでた場合、また点の並び方にクセがあらわれた場合には、工程は’管理状態にない’といい、工程に異常状態が生じていると判断して、その原因を調べて処置をとる。
ということです。
クセって何?
今回は管理図にあらわれるクセに焦点をあててみます。
このクセを理解するためには、管理図に見方と統計の知識が多少必要になります。
最初に、管理図に見方から説明します。
管理図の見方
まず以下に管理図の例を示します。
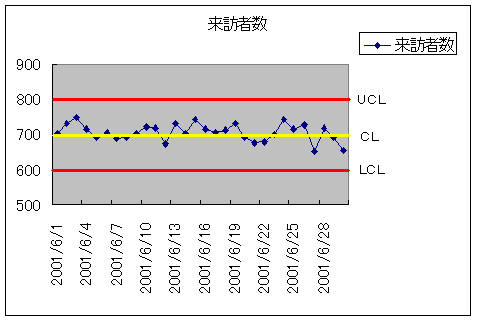
私のホームページへの来訪者数をプロットするとこんな感じになったとします。CLを700、UCLを800、LCLを600とします。ちなみに、管理図は工場の生産ラインなんかで使うのですが、それでは私が書いていて面白くないので、こういう例を示します。
この管理図を見ると、プロットした点は管理限界線(UCLとLCLです)の外には出ていませんし、クセとやらもなさそうなので、管理状態にあると言えます。
次にお正月あたりの状況を見てみます。
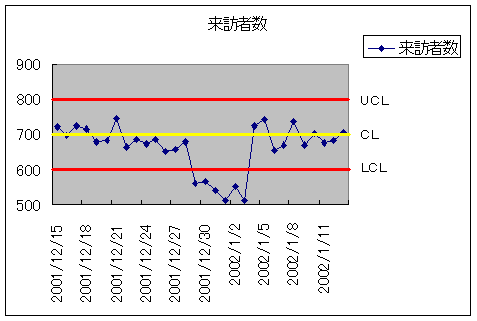
年末年始に管理限界線(LCL)を下回っています。何が起こったのでしょうか?
年末年始は会社が休みで、さらに帰省してしまうので、みんなインターネットに接続しないからです。
と、異状が起こったら分析して、工程が正しい状態になるように工程を見直します。まあ、この例では見直しようはありませんが。
では、次にクセがある場合の例を示します。
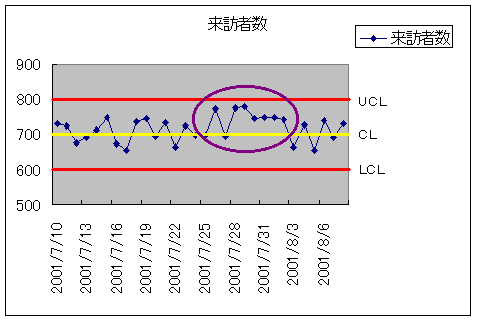
さて、この図ではプロットした点は管理限界線を超えていませんが、紫で○をつけた部分は怪しいです。
プロットした点は、いつもは黄色の線の上だったり下だったりしているのに、紫で○をつけた部分では点が黄色の線より継続して上にあります。これがクセというものです。さて、なんで点が継続して黄色の線の上にあるのでしょうか?
7月の第三週の日曜は電気通信主任技術者の試験があるので、解答例を求めてインタ−ネットをさまよっている方が私のページにアクセスするためです。
と、クセがあったら分析して、工程が正しい状態になるように工程を見直します。まあ、この例では見直しようはありませんが。
他にもいろろクセと呼ばれるものはあるのですが、それはQCの本なんかを立ち読みしてください。
管理図にクセをみつけるための統計の知識
どういう状態をクセというか? を知るためには、統計の知識が多少必要です。
まず、正規分布という分布を知ってもらいます。
正規分布と正規分布から離れてしまったグラフ
正規分布といわれたらまずこの図のグラフの形を思い浮かべてください。
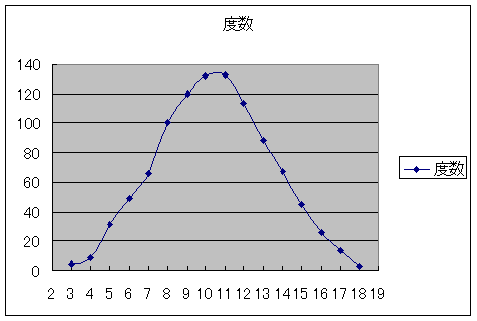
本当は難しい式を使って書かないと駄目なんですけど、面倒だし、そんなソフト(mathematicaみたいなやつ)をもってないのでサイコロ3つを1000回振って出た値を足したものをグラフにしてます。
まずこのグラフの見方を説明します。横軸がサイコロの目を足した値(サイコロ3個を振っているので、出る値は3〜18です)、縦軸がサイコロの目を足した値が出た回数です。例えば、10の目は130回くらいでてます。6の目は50回くらいしか出ていません。
さて、私の仕事がサイコロ3つをひたすら振って出た値をメモするというものだったとします。
サイコロが正常なサイコロであれば、上のグラフのように綺麗に山のような形になります。
ちなみに、ここでこのグラフを見て、真中が10.5あたりなので管理図を作るとしたら、CLを10.5に設定します。そして、サイコロの目がとりうる値は3〜18ですので、UCLを18、LCLを3に設定するのが妥当でしょう。
ここで誰かが私を陥れるためにサイコロをすりかえて、3つあるサイコロのうち1つを「2〜7」の目が出るサイコロに置き換えたとします。鈍感な私はサイコロがすり返られたことの気づきません。さて、分布はどうなってしまうのでしょうか?
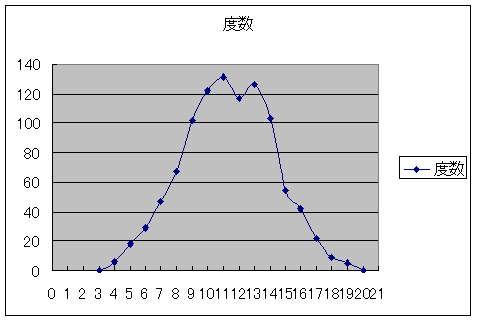
グラフを見ると、19というありえない目が出ています。私はここで異状に気づくわけです。私は工程を検査しサイコロがすりかえられいることに気がつきます。なんてこった。私はサイコロを元に戻し、仕事に励みます。
ちなみに、管理図を書いていれば、UCLを超える値がでたということで’管理状態ではない’ことが分かります。
さて、またまた誰かが私を陥れるために、サイコロをすりかえて、3つあるサイコロのうち1つを「1〜5」の目しかでないサイコロに置き換えたとします。もちろん鈍感な私ですからサイコロがすり返られたことの気づきません。さて、分布はどうなってしまうのでしょうか?
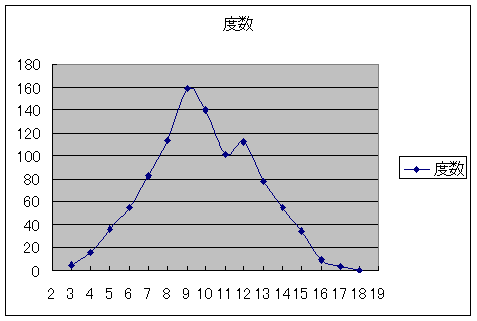
グラフを見ると、正規分布のグラフに比べると左に偏っています。私はここで異状に気づくわけです。私は工程を検査しサイコロがすりかえられいることに気がつきます。なんてこった。私はサイコロを元に戻し、仕事に励みます。
ちなみに、管理図を書いていれば、プロットした点がCLより常に下目にでてしまうでしょう。
管理図と正規分布のグラフの関係
さて、サイコロを振るたびにいちいち値をメモして集計してグラフにして分析すると手間がかかりますし、データを時間の流れで見ることができません。
そこで、サイコロを振るたびにメモしないで、10回に1回(5回に1回とかでもいいですが)メモするだけにして、横軸に時間、縦軸に度数をとることにしました。それが管理図です(と私は書いていてそう思いました)。
クセの話にもどります。工程が正常なら、管理図にデータをプロットすると適当の値がばらつくのですが、工程が異状ですとサイコロがすり返られた時のように値がCLより継続的に下めにでたり、管理限界線を越えたり、またサイコロが1と6しか出ないように細工されていたりするとプロットした点が上下に激しく行ったり来たりします。そういう状態のことをクセがあると言います。
終わりに
さて、資格を取得するだけであれば、クセってなんだ?と考える暇があったら、「ああ、クセがあったら駄目なのね」と鵜呑みにした方が早いです。電気通信主任技術者試験ではグラフをいくつか示されて「どれがクセですか?」なんて選ばされる問題はでないでしょう。





